Fórum: GEOMETRIA

Üdvözlet! Ha valakinek van egy kis ideje kérem segítsen hogyan oldható meg ez a számomra bonyolult feladat! Nagyon fontos lenne!Kérlek titeket!Előre is köszi! A feladat: Ábrázoljuk a PQR háromszög köré írt kört. Szerkesszük meg a lényeges átmérők mindkét képét a végpontokhoz tartozó érintőkkel együtt, és állítsuk elő az érintőket a háromszög csúcsaiban is. Rajzoljuk meg a vetületi görbéket. P(45, 140, 265); Q(45, 40, 205); R(145, 140, 205).

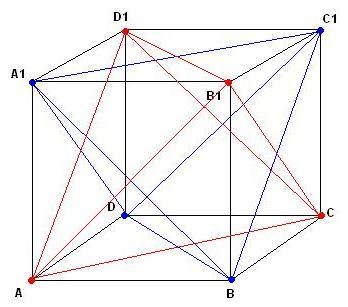
A piros tetraédet - pontosabban annak B₁-ben összefutó három lapját - a kék tetraéder A₁BC₁ lapja egy szabályos háromszögben metszi. A háromszög oldalai az ABB₁A₁ , BCC₁B₁ és A₁B₁C₁D₁ lapok középpontjait egymással összekötő három szakasz. Az alakzat szimmetriája miatt ez mind a nyolc csúcsról megállapítható. A közös részt tehát 8 szabályos háromszög határolja. A neve oktaéder. Lásd pl. http://mbuttons.bolyai.hu/upload/VRML/palyazat/kapcs.htm : Egy kocka megfelelő lapátlói szabályos tetraédert alkotnak. A két így kapott tetraéder közös része egy szabályos oktaéder.

zsolla feladatának megoldása engem is érdekelne, van rá egy gondolatom, csak 2 pontom helyzete bizonytalan. Tudtok segíteni? Itt egy gyorsan összedobott ábra:

133: Én most hirtelen csak a P-t látom: ABG háromszög egybevágó BCD háromszöggel, hiszen BG=BC, AB=BD és ABGszög= CBDszög (derékszög). Mivel AB merőleges DB-re és BG merőleges BC-re, AG-nek is merőlegesnek kel lennie CD-re. Tehát az APCszög derékszög, így az APC háromszög derékszögű. Thalesz miatt pedig a P pontnak rajta kell lennie a k3 körön. A többin még agyalok. :)

Keresem a következő feladat megoldását: Az ABCD A1B1C1D1 kocka A C B1 D1 csúcsai és az A1 C1 B D csúcsai is egy-egy tetraédert határoznak meg. Milyen test lesz a két tetraéder közös része?

Érdekesség a 133. feladathoz: Az A-t és C-t rögzítsük! B-t mozgatva AB-n a kapott DR egyenesek átmennek egy közös ponton.

Fogalmazzuk meg a fentinek megfelelő másik állítást is!

Igazoljuk az állítást!

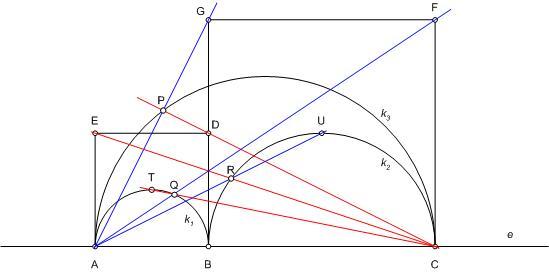
133.feladat-nak javaslom az alábbit: Egy e egyenes 3 pontja ebben a sorrendben A, B és C. Vegyük fel az egyenes egyik oldalán a T középpontú ABDE és az U középpontú BCFG négyzeteket, valamint az AB átmérőjű k₁ , BC átmérőjű k₂ és AC átmérőjű k₃ félköröket.

a) Igazoljuk, hogy az AG és CD egyenesek P metszéspontja k₃-ra, az AU és CE egyenesek R metszéspontja k₂-re, az AF és CT egyenesek Q metszéspontja k₁-re esik.

b) Mi jellemzi a P, Q, R ponthármast?

Az itteni 132. feladat egy - inverzióval történő - megoldása látszik a "Valaki mondja meg!" témában lévő [479]. hozzászólásából. Néhány "elemibb" már itt, az előző hozzászólásokban megszületett. Köszönöm!

Ha az elemibb megoldást a 3 érintkező kört érintő kör szerkeztésére gondolod, egyelőre nem látom az utat. A Geometriai feladatok gyűjteménye az általános Apolloniusz feladatot oldja meg középiskolában tanult módszerekkel:

-az adott és a szerkesztendő körök növelésével-zsugorításával visszavezeti a feladatot két kört (k₁,k₂) érintő, adott P ponton áthaladó k_e kör szerkesztésére - F2 ( elfajuló esetekben egy kör és két pont, illetve 3 pont)

-F2 megoldása során megszerkeszti a körök egyik hasonlósági pontját P-vel összekötő egyenesnek másik, k_e-re illeszkedő pontját (Q)

-Végül megszerkeszti a két adott ponton (P, Q) áthaladó, pl. k₁-et érintő kört. Ez a megoldás elemibb abban az értelemben, hogy nem használ inverziót, viszont sokkal hosszadalmasabb. És ami a fő baj, nem használja ki azt a speciális helyzetet, hogy a 3 adott kör érinti egymást. F2 megoldása során előjönnek az érintési pontok és a hasonlósági pont közötti kapcsolatok, de nem látom, esetünkben hogyan lehetne alkalmazni.

Hát igen, a hasonlósági pont :-( Ezt illett volna tudnom. A körrel kapcsolatban másnak is utánanéztem itt.

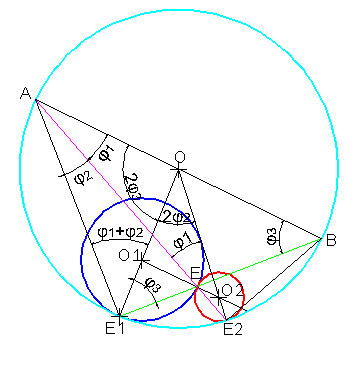
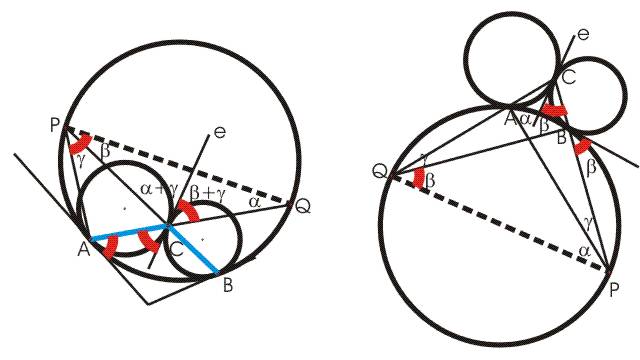
Jelölje az átmérőgyanús pontokat P és Q. A PQ ívet a két érintési pont, A, B három körívre bontja, az ezekhez tartozó kerületi szögek legyenek , és . Ekkor a CPQ háromszög szögösszege 2+2+2, mert az e közös érintő a C-nél lévő szöget a bal oldali ábrán (+) és (+) részre, a jobb oldali ábrán és részre osztja (a sima és az elfajult kerületi szögek egyenlőségét kell a közös érintőknél figyelembe venni). Tehát 2+2+2=180^o, azaz a három körív együtt egy félkört alkot.

Elnézést a többszörös beírásért, az előző három, képtelen hozzászólásomat ki is lehetne törölni. Ha egy moderátor olvassa, köszönöm előre is. (törölve - Sirpi)

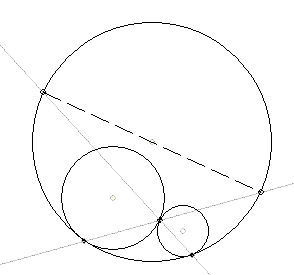
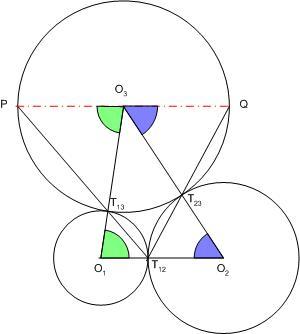
Az állítás abból adódik, hogy két érintkező kör érintési pontja egyben a két kör kölső vagy belső hasonlósági pontja is. Talán jobban áttekinthető kívülről érintkező körökre, ekkor az érintési pont belső hasonlósági pont. Az ábrán a hasonlóság miatt PO₃||T₁₂O₁ésQO₃||T₁₂O₂. Mivel O₁,O₂ésT₁₂ egy egyenesen vannak, ezért P,QésO₃ is, vagyis PQ a kör átmérője.

Igen, látom. Például a ₃ esetében: ha a kerületi és középponti szögek összefüggését vizsgálom, akkor AB-ról még nem feltételeztem, hogy átmegy O-n. Viszont amikor az E₁BO háromszögben az alapon fekvő szögekről állítom, hogy ₃, akkor már igen. Ellenben úgy tűnik, O₁O₂ párhuzamos az OB-vel.

Nem használtam fel azt, hogy az E érintési pont. Lehet, hogy felhasználtam a bizonyításban a bizonyítandó állítást?!

Így túl elemi volna...

Azt kell igazolni, hogy az A, O és B pontok egy egyenesen vannak. Elég belátni, hogy AE₁B =90 (E₁ az AB Thalesz körén van, tehát AB egy átmérő).

Először a kerületi és középponti szögek összefüggéseit, valamint az egyenlő szárú háromszögek alapon fekvő szögeinek egyenlőségét használjuk ki. Ezzel adódnak az ábrán látható szögek.

Az AOE₂ háromszögben: 2₁+2₂+2₃=180, tehát ₁+₂+₃ = 90.

AE₁B = (₁+₂)+₃= 90, így az állítást igazoltuk.

A feladat Hoa a "Valaki mondja meg!" témában lévő [479]. hozzászólásából adódott. Remélem "elemibb" megoldás is születik rá!

Ez meglepő.

Ábra a 132. feladathoz:

132. feladat: Három kör páronként érinti egymást három, nem egy egyenesen lévő pontban. Két kör érintési pontján át húzzunk egy-egy egyenest a másik két ponton át! Bizonyítsuk be, hogy ezeknek a harmadik körrel való másik metszéspontja a kör két átellenes pontja!

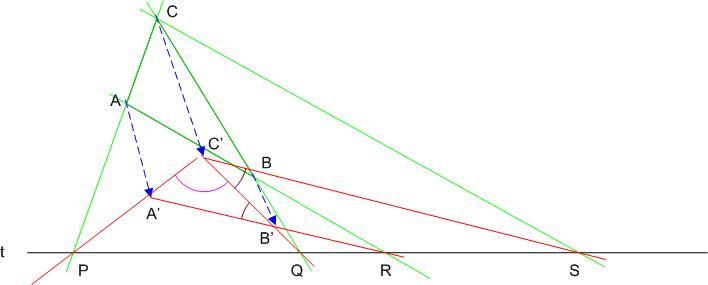
Legyen A'B'C' az ABC háromszög képe az affinitásnál. Ekkor A'B'C' oldalegyenesei is a P, Q, R pontokban metszik a t tengelyt. Az affinitás párhuzamosság-tartró tulajdonsága miatt C'S és A'R párhuzamosak. Ezért A'B'C' szög és B'C'S szög váltószögek, egyenlőek. Így C' pontból a QS szakasz az egyik adott (béta), PQ pedig a másik adott - én C'-nél lévő szög miatt gammának nevezném - szög alatt látszik. Ebből a leírt szerkesztés már adódik.

Köszönöm!

Köszönöm szépen.

Kijött. :)

Ha geometriai feladatról van szó, vegyük fel a Q pontot tartalmazó, PQ szakaszra merőleges S síkot. Ebben a síkban rajzoljunk egy Q középpontú, 35 mm oldalú négyzetet. A négyzet csúcsai és P alkotják a keresett gúlát.

Ha ábrázoló geometria, akkor javaslom, tedd fel abba a fórumba.

Kedves Cocka!

Egyelőre, hogy ne bosszankodj tovább, a válasz kérdésedre: az adott látószögű köríveket PQ és QS fölé kell rajzolni. Itt most nincs rajzoló programom, úgyhogy ábra és indiklás holnap.