|
|
|
| [1072] kromers | 2008-06-18 14:13:43 |
 Szép napot mindenkinek! Egy kis segitségre lenne szükségem. Adott egyenessel adott ponton át párhuzamos egyenes szerkesztése. A szerkesztés menetének több változata is ismeretes. A problémám a következő, hol találom meg ezeknek a BIZONYITÁSÁT? Előre is köszönöm
|
|
| [1071] Euler | 2008-06-18 14:07:27 |
 Nekem is van egy megoldásom, sajnos ehhez is kell trigonometria, de azért érdermes megnézni:(nem tudok képleteket beírni, így egy kicsit hülyén fog kinézni) szorozd be mindkét oldalt 2cos20-al, vedd észre a sin(2x)=2sinxcosx addicios tételt, majd a sin40 négyzetére ismert addicios összefüggést használd( 2sinx.sinx=1-cos(2x). Ezekután ismételten használd a sin160=2sin80cos80 összefüggést, sin160=sin20, kapod, hogy sin80=1/2sin20+(gyök3)/2.cos20, ez pedig nyilván igaz, hiszen a jobb oldalon sin(x+y) áll.
|
| Előzmény: [1067] S.Ákos, 2008-06-17 20:28:38 |
|
|
|
|
| [1067] S.Ákos | 2008-06-17 20:28:38 |
 Valaki tudna mutatni egy elemi geometriai megoldást az alábbi feladatra: Bizbe, hogy 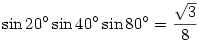 ? ?
|
|
| [1066] bronco | 2008-06-12 01:34:40 |
 Neked is köszönöm szépen, sokat segítettél!
|
|
| [1065] Csimby | 2008-06-11 23:36:54 |
 segítség A pontokat mozgatni lehet. Ha kettőt egymásra teszel, akkor épp 5 érintőt kapsz és abból már látszik hogy kell a szerkesztést csinálni. (veszed az 5 egyenes által meghatározott 5-szöget, kiválasztod az egyik a oldalát, két szomszédos oldal legyen b és c. A b és c re eső 4 csúcsot "keresztbe" összekötöd, a metszéspon legyen M. Ekkor M-en és az a-val szemben lévő csúcson átmenő egyenes kimetszi a-ból az a-ra eső érintési pontot)
|
| Előzmény: [1064] bronco, 2008-06-11 23:21:28 |
|
| [1064] bronco | 2008-06-11 23:21:28 |
 Sziasztok!
Egy projektív geometriai feladatban lenne szükségem segítségre:
Adott egy kúpszelet öt érintőegyenese. Szerkeszzük meg az egyiken az érintési pontot!
Egyszerűnek tűnik, de sehol sem találok hasonló megoldott feladatot. (Annyi tudok, hogy a Brianchon-tétel elfajuló esetét kell alkalmazni.)
Előre is köszi!
|
|
|
| [1062] SmallPotato | 2008-06-05 11:53:17 |
 A feladat értelmében a paralelogramma egyik átlója adott (a kör sugara), továbbá szögei is adottak.
Rajzoljuk fel az ismert átlóra az ismert szög látókörét. Az átló végpontjai és a látókör-ív egy futó pontja olyan háromszöget határoznak meg, amelynek területe a paralelogramma területének fele. E háromszög területe viszont akkor maximális, ha a rögzített oldalhoz tartozó magassága maximális, azaz a látókör-ív felében álló harmadik csúcs esetén. Eszerint a paralelogramma területe ott maximális, ahol a paralelogramma oldalai egyenlők, azaz ha a paralelogramma rombusz, vagyis ha a hiányzó negyedik csúcs a körcikk ívének felezőjében van.
|
| Előzmény: [1061] Euler, 2008-06-05 11:30:15 |
|
| [1061] Euler | 2008-06-05 11:30:15 |
 Hello mindenkinek! Van egy geometria feladatom, melyre teljesen elemi geometriai megoldást szeretnék hallani, már kijött trigonometriával, de léteznie kell elemi geos megoldásnak is. Ha valakinek van ötlete, legyen szives ossza meg velem is! Előre is köszi, a feladat: Adott egy körcikk, melynek középponti szöge hegyesszög. A körcikkbe olyan paralalogrammákat irunk, amelynek oldalai párhuzamosak a szögszárral, egyik csúcsa a szögcsúcs, 2 a szárakon van és a negyedik a köríven. Mikor maximális a területe a paralelogrammának?
|
|
| [1060] BohnerGéza | 2008-06-05 10:52:40 |
 Nem! Kellett és szép volt a megoldásod! Ez utóbbi megoldás, csak a 134/a feltételei mellett megy.
Egymást metsző köröket nem lehet koncentrikussá képezni, illetve, ha a két egymást nem metszö körhöz tartozó mindkét nullkörön átmegy a harmadik, akkor annak képe egyenes lesz.
|
| Előzmény: [1059] HoA, 2008-06-05 00:02:58 |
|
| [1059] HoA | 2008-06-05 00:02:58 |
 Hát igen. És ezek szerint jól sejtettem, hogy a 134. feladat megoldása is ez: legyen I az az inverzió, amely k1 -et és k2 -t koncentrikus körökbe képezi le, ekkor akárhová is esik k3' középpontja, a három körközéppont valójában kettő, és így egy egyenesen vannk.
|
| Előzmény: [1058] BohnerGéza, 2008-06-04 20:29:36 |
|
|
| [1057] HoA | 2008-06-04 15:52:46 |
 Csak nem az a galád trükk lett volna a 134. feladat eredeti megoldása, hogy ha három pontból kettő egybeesik, akkor egy egyenesen vannak? Az eredeti kitűzésbe ez is belefér. A 135. feladat ábrája ismerős a "Fejezetek az elemi geometriából" c. könyvből. Ez az ottani feladat általánosítása. Eredetileg azt kellett igazolni, hogy ha "1" valamilyen helyétől indulva a körsorozat n körből áll és "n" érinti "1" -et, akkor ez "1" tetszőleges helyéről indulva is fennáll. A kapcsolatot 134. -gyel ott vélem felfedezni, hogy 135. megoldásának kulcsa is két egybeeső körközéppont.
|
| Előzmény: [1056] BohnerGéza, 2008-06-04 12:50:33 |
|
|
| [1055] HoA | 2008-06-04 10:00:34 |
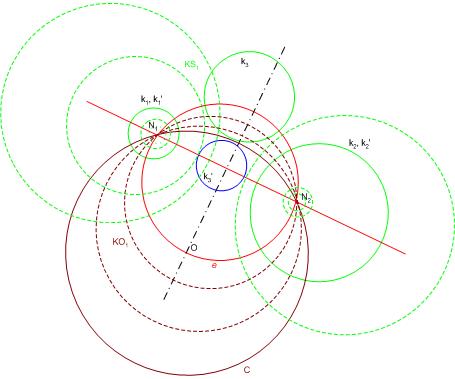
 A 134/a feladat megoldása: Az egymást nem metsző k1 és k2 körök által maghatározott körsor legyen KS1 , nullkörei N1 és N2 . k3 ne haladjon át N2-n, a k3 és N2 által maghatározott körsor legyen KS2 , ennek másik nullköre N3 , a keresett inverzió I, alapköre C, ennek középpontja O. Mivel egy elliptikus körsor köreinek középpontjai a nullkörök által meghatározott egyenesen vannak, köreink inverzeinek, k1',k2'ésk3' köröknek a középpontjai csakkor lesznek egy egyenesen, ha N1' N2' és N3' is. N1' és N2' e1' egyenese I-nél a KS1 körsor ortogonális korsora, KO1 azon ko1i körének lesz az inverze, amelyik O-n áthalad, vagyis az N1 , N2 és O pontok által meghatározott körnek. Hasonlóan N2' és N3' e2' egyenese a KS2 körsor ortogonális korsora, KO2 azon ko2j körének lesz az inverze, amelyik O-n áthalad, vagyis az N2 , N3 és O pontok által meghatározott körnek. e1' és e2' tehát csakkor azonos, ha ko1i és ko2j azonosak, vagyis ko1i = ko2j az N1 , N2 és N3 pontok által meghatározott kör, melyre O is illeszkedik. Ez persze az ortogonalitás miatt megegyezik [1049] e körével, így a megoldás folytatható az ott leírtak szerint, a nullkörök és körsorok megszerkesztése nem szükséges. Az egyszerűbb gyakorlati kivitelezést eredményező O és C megválasztás ebben a terminológiában úgy fogalmazható, hogy legyen C a KO1 azon köre, melynek O középpontja e -re illeszkedik. Ekkor KS1 inverze önmaga.
|
 |
| Előzmény: [1053] BohnerGéza, 2008-05-30 23:09:00 |
|
| [1054] HoA | 2008-06-02 13:42:59 |
 További segítségként a 134/a feladathoz feloldom az [1048]-beli észrevételt: Két kör által meghatározott körsor nullköreinek inverze adott inverziónál megegyezik a körsor inverzének nullköreivel.
|
| Előzmény: [1053] BohnerGéza, 2008-05-30 23:09:00 |
|
| [1053] BohnerGéza | 2008-05-30 23:09:00 |
 Pontosítom a feltételt, ezzel segítek is: 134/a feladat: A 134. feladatban tegyük meg ezt a kikötést: a 3 kör közt van kettő, melyek nem metszik egymást, és az általuk meghatározott körsor legalább egyik nullkörén nem megy át a harmadik kör. Ekkor HoA előbbi megoldásán túl adódik egy másik megoldás is.
|
| Előzmény: [1052] BohnerGéza, 2008-05-28 20:19:50 |
|
|
| [1051] BohnerGéza | 2008-05-28 20:13:06 |
 Köszönöm HoA megoldását, egyben kitűzöm könnyítve a feladatot:
134/a feladat: A 134. feladatban tegyük meg azt a kikötést, hogy a 3 körnek nem lehet közös pontja. Így az előbbi mo-tól eltérő is megadható!
|
| Előzmény: [1050] HoA, 2008-05-28 08:11:09 |
|







 képlet itt is kell.)
képlet itt is kell.)




