| [1116] Lowosan | 2008-09-03 19:41:43 |
 távolságuk kell elfelejtettem odairni
|
|
|
|
| [1113] Lowosan | 2008-09-03 15:30:33 |
 Helló Segitségre lenne szükségem a kordinátageometria területén e:3x+2y=12 f:6x+4y=-12 ezt hogy kéne megoldani? mert új matektanárunk van és nem magyaráz semmit csak annyit mond csináljunk meg semmi más
|
|
| [1112] farkasb | 2008-09-03 13:16:31 |
 Kedves Mihály!
Köszönöm a gyors választ, megpróbálkozok a feladattal. Esetleg nem tudna ajánlani valami jó megoldást legjobban illeszkedő sík elkészítésére? A hibák az x y és z koordinátákat is terheljék. Köszönöm!
|
| Előzmény: [1111] Fálesz Mihály, 2008-09-02 21:45:36 |
|
| [1111] Fálesz Mihály | 2008-09-02 21:45:36 |
 Vaughan Pratt munkája nyomán a következőt tudom ajánlani. (Én magam is sokszor haszáltam ezt a módszert kör, gömb és henger illesztésére.)
Keressük a kör egyenletét
| f(x,y)=A(x2+y2)+Bx+Cy+D=0 | (1) |
alakban, ahol
Egy kis számolás után látható, hogy a (2) feltétel azzal ekvivalens, hogy a kör sugara 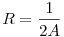 , illetve az f(x,y) függvény gradiense a körvonalon egységnyi hosszú. , illetve az f(x,y) függvény gradiense a körvonalon egységnyi hosszú.
Ha (x,y) egy pont a körvonalhoz közel, akkor |f(x,y)| jól közelíti a pont és a körvonal távolságát.
Legyenek a mintapontok (x1,y1),...,(xn,yn). Az illesztés négyzetes hibája közelítőleg
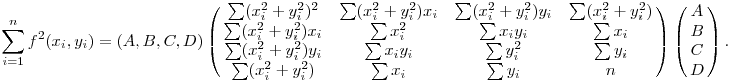 | (3) |
Szóval a (3) kifejezés minimumát keressük a (2) feltétel mellett. Ha ráereszted a Lagrange-multiplikátor módszert, kapsz egy 4-dimenziós sajátértékfeladatot, ráadásul a keresett sajátérték pont a hiba konstansszorosa...
Ha a (2) helyett az A=1 feltételt használod, akkor a számolás sokkal egyszerűbb, mert csak lineáris egyenletszert kell megoldani. Ennek a gyengéje, hogy a (3)-ban a hibát megszoroztad kb. 4R2-tel. Zajos adat esetén nagyobb lesz az illesztés valódi hibája, de kisebb lesz a sugár, amivel megszorzod.
|
| Előzmény: [1110] farkasb, 2008-09-02 09:00:28 |
|
| [1110] farkasb | 2008-09-02 09:00:28 |
 Kedves Fórumozók!
Ismételten egy kérdést tennék fel:
Hogyan határozható meg egy olyan kör középpontja, ami n számú xy koordinátával adott pontra legjobban illeszkedik? Előre is köszönettel: farkasb
|
|
| [1109] BohnerGéza | 2008-09-02 01:25:18 |
 Fálesz Mihály a [1105]-ban fölvetette, hogy egy számolás nélküli megoldás szép lenne. Egyelőre nincs hozzá ötletem. A 137/b és 137/c feladat tulajdonképpen megoldása a 137-nek, igaz végig kell gondolni. (Számolással egyszerűbben is megy [1106].)
|
 |
| Előzmény: [1108] BohnerGéza, 2008-08-28 23:51:38 |
|
|
| [1107] HoA | 2008-08-28 17:10:45 |
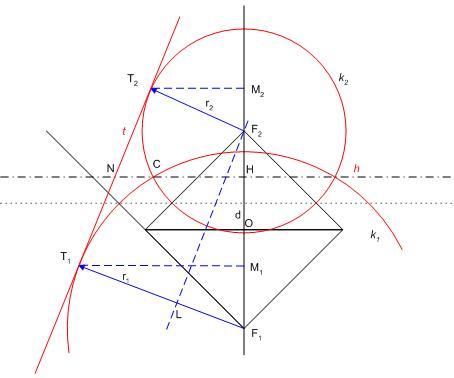
 Még tart a nyári szünet... 137/b feladat megoldása: Legyen az F1F2 távolság 2f , F1F2 felezőpontja O. Az F1 középpontú r1 sugarú k1 és az F2 középpontú r2<r1 sugarú k2 körök h hatványvonala messe F1F2-t H -ban. Határozzuk meg az OH távolságot f,r1ésr2 ismeretében. Legyen k1ésk2 közös érintője t , az érintési pontok T1ésT2 , a Ti -ből F1F2 -re bocsátott merőleges talppontja Mi , az F2-n át t-vel húzott párhuzamos és F1T1 metszéspontja L, t és h metszéspontja N. F1L=r1-r2 Az F1M1T1,F2M2T2ésF1LF2 derékszögű háromszögek hasonlóak, 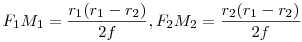 . . 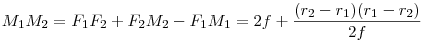 . .
N felezi T1T2 -t ( egyenlő érintőszakaszok ) , ezért H is felezi M1M2-t. 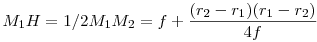 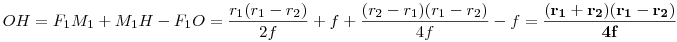 . Feladatunkban . Feladatunkban 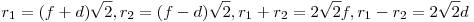 , igy , igy 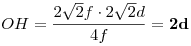 . .
|
 |
| Előzmény: [1106] BohnerGéza, 2008-08-24 23:37:33 |
|
| [1106] BohnerGéza | 2008-08-24 23:37:33 |
 Tetszik az affinításos és a többi megoldás is.
Így a 137. feladat általánosításával - miszerint a középvonal 1:1 aránya helyett más arányban osztó szakaszt adunk meg a magasságpont számára - kapott feladat is könnyen bizonyítható.
Érdemes persze Fálesz Mihály ajánlata alapján, igaz számolással, az ellipszis definíciója alapján is elvégezni a bizonyítást!
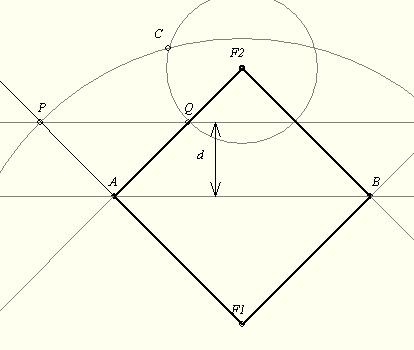
137/b. feladat: Az A, F1, B, F2 pontok egy négyzet csücsai. Az AC átlóval párhuzamos - tőle d (<>0) távolságra húzott egyenes messe az AF1-t P, az AF2-t Q-ban. Legyen C az F1 kp-ú P-n és az F2 kp-ú Q-n átmenő kör kp-ja. Mutassuk meg, hogy C 2d távolságra van AC-től! (Milyen d esetén vam C pont?)
|
 |
| Előzmény: [1105] Fálesz Mihály, 2008-08-18 10:54:25 |
|
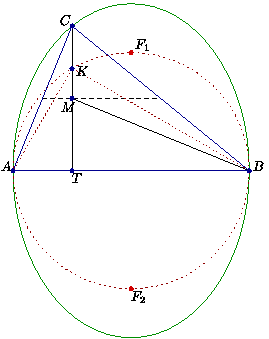
| [1105] Fálesz Mihály | 2008-08-18 10:54:25 |
 Legyen M a magasságpont, és T a C-ből induló magasság talppontja. Mint jól ismert, TC . TM = - TA . TB. (Ez azért igaz, mert a magasságpontnak az AB oldalra vonatkozó tükörképe a körülírt körön van, de például az ATC és MTB háromszögek hasonlóságából is láthatjuk.)
Ha az M pont a középvonalon van, akkor TC és TM azonos irányú, TA és TB pedig ellentétes írányú, vagyis T az AB szakasz belsejében van. A TC félegyenes tehát metszi az AB átmérőjű kört; legyen K a metszéspontjuk.
Fálesz Mihály tétele szerint BKA =90o, a magasságtételből pedig TK2=AT . TB. =90o, a magasságtételből pedig TK2=AT . TB.
Így tehát TC2=2.TC.TM=2.TA.TB=2.TK2 és
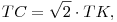
a C csűcs azon az ellipszisen van, amit az AB átmérőjű körből kapunk az AB tengelyű, 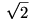 arányú merőleges affinitással. arányú merőleges affinitással.
Az A és B pont kivételével az ellipszis bármelyik pontjából kiindulva a gondolatmenet megfordítható.
* * *
Eleminek ezt a megoldást sem nevezném, bár az eredmény alapján nehéz ennél "elemibbet" várni. Aki akarja, megpróbálhatja -- számolás nélkül!!! -- bebizonyítani, hogy F1C+F2C=F1A+F2A, csak ezzel meg az a bajom, hogy az eredményt valahonnan máshonnan tudtuk meg.
|
 |
| Előzmény: [1104] HoA, 2008-08-15 15:20:47 |
|
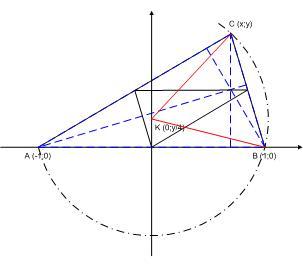
| [1104] HoA | 2008-08-15 15:20:47 |
 Ne feledkezzünk meg a 137. feladatról. Kedvcsinálónak BohnerGéza sejtésének igazolása. Ha a magasságpont az FaFb középvonalon van, akkor a körülírt kör K középpontja a középponti háromszög középvonalán van, tehát K távolsága a c oldaltól negyede mcnek. Az általánosság megszorítása nélkül legyenek A, B és C koordinátái (-1;0) , (1;0) és (x,y) . Ekkor K =(0;y/4) . KB = KC -ből a távolságok négyzetére
1+(y/4)2=x2+(3y/4)2
. 1+y2/16=x2+9y2/16 ; 1=x2+8y2/16

A C pontok egy ellipszisen helyezkednek el. Várjuk az elemi geometriai megoldásokat!
|
 |
| Előzmény: [1085] BohnerGéza, 2008-07-20 21:50:08 |
|
|
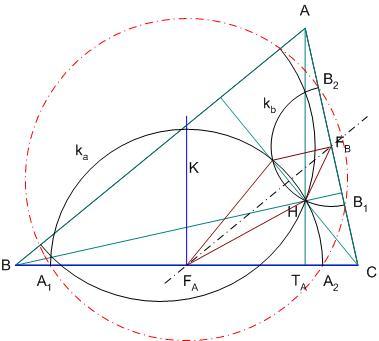
| [1102] HoA | 2008-08-12 16:42:59 |
 Köszönöm, kitűnő gondolat. Pedig már az ábrán is látszott... Mivel ka és kb egyik metszéspontja H, hatványvonaluk a H-n áthaladó, FAFB-re merőleges egyenes, vagyis mc. C rajta van a hatványvonalon, CA1.CA2=CB1.CB2, vagyis A1,A2,B1,B2 egy körön van.
|
 |
| Előzmény: [1100] Fálesz Mihály, 2008-08-12 09:22:15 |
|
|
|
| [1098] Káli gúla | 2008-08-11 21:23:53 |
 A 9-es szorzót trigonometria nélkül is megkaphatjuk: Ha a,b,c három egységvektor, azaz |a|=|b|=|c|=1, akkor
(a-b)2+(a-c)2+(b-c)2=2(a2+b2+c2)-2ab-2ac-2bc=3(a2+b2+c2)-(a+b+c)2=9-(a+b+c)2 9 . 9 .
Egyenlőség pontosan akkor van, ha a+b+c=0. Ugyanígy, n darab egységvektor közötti összes távolság négyzetösszege legfeljebb n2 (és egyenlőség csak 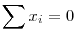 esetén lehet): esetén lehet):
![\sum_{i<j} (x_i-x_j)^2 =
\sum_{i<j} (x_i^2 + x_j^2) - \sum_{i<j} 2 x_i x_j
= (n-1) \sum x_i^2 - \left[(\sum x_i)^2 - \sum x_i^2\right]=
n^2 - (\sum x_i)^2 \le n^2](keplet.cgi?k=5E235FB51CBD26E2)
|
| Előzmény: [1093] BohnerGéza, 2008-08-05 20:34:02 |
|
|
| [1096] HoA | 2008-08-08 12:06:40 |
 [1096] - hoz hasonlóan a cosinus tételből kiindulva kicsit körülményesebben is erre az eredményre juthatunk :-) . Az adott körbe írt H0 háromszögben, mint [1096] ábráján is , legyen  a nagyságra középső szög, a nagyságra középső szög,      . Ekkor . Ekkor 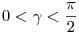 . Rögzítsük c-t , és így . Rögzítsük c-t , és így  -t is . a2+b2+c2=2.c2+2abcos -t is . a2+b2+c2=2.c2+2abcos . Ez cos . Ez cos >0 miatt annál nagyobb, minél nagyobb az ab szorzat. A sinus tételből >0 miatt annál nagyobb, minél nagyobb az ab szorzat. A sinus tételből 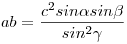 , tehát elég sin , tehát elég sin sin sin változását vizsgálni. A szorzatot összeggé alakítva sin változását vizsgálni. A szorzatot összeggé alakítva sin sin sin =1/2{cos( =1/2{cos( - - )-cos( )-cos( + + )} . Állandó )} . Állandó  mellett mellett  + + is állandó, a két szög különbségének cosinusa pedig annál nagyobb, minél kisebb a két szög különbsége. Eljutottunk [1096] eredményéhez: C -t a körülírt körön az AB ív F felezőpontja felé mozgatva is állandó, a két szög különbségének cosinusa pedig annál nagyobb, minél kisebb a két szög különbsége. Eljutottunk [1096] eredményéhez: C -t a körülírt körön az AB ív F felezőpontja felé mozgatva  - - csökken és így az oldalak négyzetösszege nő. csökken és így az oldalak négyzetösszege nő.
Mindkét megközelítésre vonatkozó megjegyzés: Szigorúan véve csak azt mutattuk meg, hogy ha van az oldalak négyzetösszegének maximuma, az csak a szabályos hármszögben lehet. Kis finomítással bizonyítható a maximum létezése. H0-ban  >60o és >60o és  <60o , mint a háromszög legnagyobb ill. legkisebb szöge. Ha C -vel F -be jutunk, a másik két szög egyenlő lesz, tehát áthaladtunk egy olyan C' pozíción, ahol a két szög egyike éppen 60o . Legyen ez a háromszög H1 . H1 -ben tehát az oldalak négyzetösszege nagyobb, mint H0-ban. Betűzzük át H1 csúcsait úgy, hogy itt is teljesüljön <60o , mint a háromszög legnagyobb ill. legkisebb szöge. Ha C -vel F -be jutunk, a másik két szög egyenlő lesz, tehát áthaladtunk egy olyan C' pozíción, ahol a két szög egyike éppen 60o . Legyen ez a háromszög H1 . H1 -ben tehát az oldalak négyzetösszege nagyobb, mint H0-ban. Betűzzük át H1 csúcsait úgy, hogy itt is teljesüljön      . Nyilván . Nyilván  lesz a 60o -os szög. H1 -ben c-t rögzítve és C -vel a körülírt körön mozogva az oldalak négyzetösszege az AB ív F felezőpontjában nagyobb lesz, mint H1 -ben . Ez a H2 háromszög viszont szabályos, hiszen lesz a 60o -os szög. H1 -ben c-t rögzítve és C -vel a körülírt körön mozogva az oldalak négyzetösszege az AB ív F felezőpontjában nagyobb lesz, mint H1 -ben . Ez a H2 háromszög viszont szabályos, hiszen  =60o és =60o és  = = . Tehát tetszőleges H0-ból indulva a szabályos H2 -ben nagyobb az oldalak négyzetösszege , mint H0-ban , H2 tényleg a maximumot adja. . Tehát tetszőleges H0-ból indulva a szabályos H2 -ben nagyobb az oldalak négyzetösszege , mint H0-ban , H2 tényleg a maximumot adja.
Második megjegyzés: [1096] helyes ábrájához a szövegben is meg kell említeni, hogy  -nak az egyik hegyesszöget választjuk. Ellenkező esetben nagyobb területhez kisebb (tompaszög) vagy változatlan (derékszög) oldal-négyzetösszeg tartozik. -nak az egyik hegyesszöget választjuk. Ellenkező esetben nagyobb területhez kisebb (tompaszög) vagy változatlan (derékszög) oldal-négyzetösszeg tartozik.
|
| Előzmény: [1095] BohnerGéza, 2008-08-08 01:43:50 |
|
|
|
|
| [1099] HoA | 2008-08-05 11:27:07 |
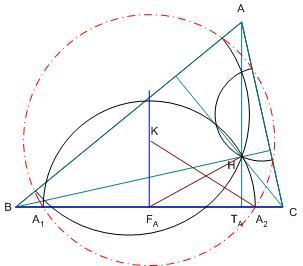
 Hát ha senkit nem érdekel... A [1087] feladat megoldása: Mivel A1A2 a keresett kör húrja, ennek felező merőlegese egyben a BC oldal felező merőlegese, tehát átmegy K-n, és ez a másik két oldalra is igaz, így ha van ilyen kör, annak középpontja csak K lehet. A javasolt segítséget felhasználva - legyen a helyvektorok kezdőpontja K - írjuk fel K és A2 távolságát, felhasználva, hogy ekkor  . Legyen BC felezőpontja . Legyen BC felezőpontja 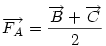 , , 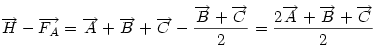 . Ennek hossza FA és A2 távolsága , ezért . Ennek hossza FA és A2 távolsága , ezért
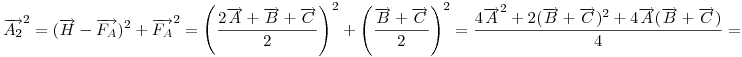

Ez a kifejezés A, B, C -ben szimmetrikus, tehát például K és B2 távolságának négyzetére ugyanezt kapnánk, a hat pont így egy K középpontú körön fekszik.
Hasonló, de trigonometriai átalakításokat igénylő megoldást kapunk, ha a feltételezett Rh körsugarat a körülírt kör R sugarával és a  szögeivel fejezzük ki. Legyen BC felezőpontja FA, ma talppontja TA . Rh2=KFA2+FAA22=KFA2+FAH2=KFA2+FATA2+TAH2 . szögeivel fejezzük ki. Legyen BC felezőpontja FA, ma talppontja TA . Rh2=KFA2+FAA22=KFA2+FAH2=KFA2+FATA2+TAH2 .
Itt KFA=R.cos , ,
BTA=2.R.sin cos cos , FATA=2.R.sin , FATA=2.R.sin cos cos -R.sin -R.sin , ,
TAH=2.R.sin cos cos .ctg .ctg =2.R.cos =2.R.cos .cos .cos . A négyzetösszeg: . A négyzetösszeg:
Rh2=R2(cos2 +4.cos2 +4.cos2 .sin2 .sin2 +sin2 +sin2 -4.sin -4.sin cos cos sin sin +4.cos2 +4.cos2 cos2 cos2 )=R2(1+4.cos2 )=R2(1+4.cos2 -4.sin -4.sin cos cos sin sin )=R2(1+4.cos )=R2(1+4.cos (cos (cos -sin -sin sin sin ))=R2(1+4.cos ))=R2(1+4.cos (-cos( (-cos( + + )-sin )-sin sin sin ))=R2(1+4.cos ))=R2(1+4.cos (sin (sin sin sin -cos -cos cos cos -sin -sin sin sin ))=R2(1-4.cos ))=R2(1-4.cos cos cos cos cos ) )
Mivel a kifejezés  , , , , -ban szimmetrikus, az első megoldáshoz hasonlóan adódik, hogy a 6 pont valóban egy K középpontú Rh sugarú körön fekszik. -ban szimmetrikus, az első megoldáshoz hasonlóan adódik, hogy a 6 pont valóban egy K középpontú Rh sugarú körön fekszik.
|
 |
| Előzmény: [1087] BohnerGéza, 2008-07-22 01:24:34 |
|
| [1092] HoA | 2008-07-23 13:35:46 |
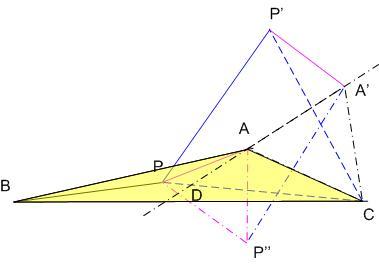
 A 136. feladat megoldása: Induljunk ki a 120o -nál nem nagyobb szögű  esetére ismert bizonyítás ábrájából. Forgassuk el a CAP esetére ismert bizonyítás ábrájából. Forgassuk el a CAP  -et az óramutató járásának irányába C körül 60o -kal, a másik két csúcs elforgatottja A' ill. P' . AA'C és PP'C -et az óramutató járásának irányába C körül 60o -kal, a másik két csúcs elforgatottja A' ill. P' . AA'C és PP'C  -ek szabályosak, AA' = AC és PP' = PC, valamint A'P' = AP , tehát azt kell igazolnunk, hogy a BPP'A' T2 törtvonal nem rövidebb a BAA' T1 törtvonalnál. Az összehasonlításnál a nehézséget csak az jelenti, hogy a két törtvonal - mint ábránkon is - keresztezheti egymást. Egészítsük ki ezért az A'P'P -ek szabályosak, AA' = AC és PP' = PC, valamint A'P' = AP , tehát azt kell igazolnunk, hogy a BPP'A' T2 törtvonal nem rövidebb a BAA' T1 törtvonalnál. Az összehasonlításnál a nehézséget csak az jelenti, hogy a két törtvonal - mint ábránkon is - keresztezheti egymást. Egészítsük ki ezért az A'P'P  -et a PA' átlójú A'P'PP'' parallelogrammává. Ekkor PP'' = P'A' és P''A' = PP', így T2 helyett vehetjük a vele azonos hosszúságú BPP''A' T3 törtvonalat. A'P' AP 60o-os elforgatottja, így a vele egyállású P''P PA-val 60o-os szöget zár be, APP'' -et a PA' átlójú A'P'PP'' parallelogrammává. Ekkor PP'' = P'A' és P''A' = PP', így T2 helyett vehetjük a vele azonos hosszúságú BPP''A' T3 törtvonalat. A'P' AP 60o-os elforgatottja, így a vele egyállású P''P PA-val 60o-os szöget zár be, APP''  szabályos, AP'' AP 60o-os órajárással ellentétes elforgatottja. Mivel AP az ABC szabályos, AP'' AP 60o-os órajárással ellentétes elforgatottja. Mivel AP az ABC  belsejében, és így a konvex BAC szögtartomány belsejében ( vagy határán ) fekszik, AP'' a BAA' konkáv szögtartomány belsejében ( vagy határán ) fekszik, ezért az APP'' belsejében, és így a konvex BAC szögtartomány belsejében ( vagy határán ) fekszik, AP'' a BAA' konkáv szögtartomány belsejében ( vagy határán ) fekszik, ezért az APP''  és így T3, a BPP''A' törtvonal is a a BAA' konkáv szögtartományba esik, P vagy P'' esetleg a határára. Legyen az AA' egyenes és T3 metszéspontja D. Jelöljük X és Y pontok T3 mentén mért távolságát tXY-nal. Ekkor tBD+DA és így T3, a BPP''A' törtvonal is a a BAA' konkáv szögtartományba esik, P vagy P'' esetleg a határára. Legyen az AA' egyenes és T3 metszéspontja D. Jelöljük X és Y pontok T3 mentén mért távolságát tXY-nal. Ekkor tBD+DA BA és tDA' BA és tDA' DA'=DA+AA' . A kettőt összeadva DA kiesik: tBD+tDA'=tBA' DA'=DA+AA' . A kettőt összeadva DA kiesik: tBD+tDA'=tBA' BA+AA', és egyenlőség csak akkor áll fenn, ha mindkét egyenlőtlenségben fennáll, vagyis ha P = P'' = A. BA+AA', és egyenlőség csak akkor áll fenn, ha mindkét egyenlőtlenségben fennáll, vagyis ha P = P'' = A.
|
 |
| Előzmény: [1078] BohnerGéza, 2008-07-15 17:42:46 |
|











 =90o, a magasságtételből pedig TK2=AT . TB.
=90o, a magasságtételből pedig TK2=AT . TB. 


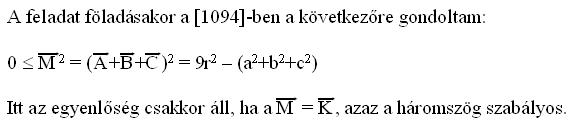

 9 .
9 .
 a nagyságra középső szög,
a nagyságra középső szög, 

 . Ekkor
. Ekkor 

 szögeivel fejezzük ki. Legyen BC felezőpontja FA, ma talppontja TA . Rh2=KFA2+FAA22=KFA2+FAH2=KFA2+FATA2+TAH2 .
szögeivel fejezzük ki. Legyen BC felezőpontja FA, ma talppontja TA . Rh2=KFA2+FAA22=KFA2+FAH2=KFA2+FATA2+TAH2 . 
