| [1169] BohnerGéza | 2009-02-04 14:46:10 |
 143. feladat: Bizonyítandó, hogy egy nem derékszögű háromszögnek és a magasságpontja oldalakra vonatkozó tükörképei által kapott háromszögnek ugyanazon ponthoz tartozó Simson-egyenese merőleges egymásra!
|
|
|
|
| [1166] edu | 2009-01-23 09:22:12 |
 Hi! A csak körzővel való szerkesztésekről keresek irodalmat. Különös tekintettel érdekelne egy adott kör középpontjának megszerkesztése (csak körzővel),ill. ennek bizonyítása (ha lehet elemi úton).A segítséget előre is köszönöm.
|
|
|
| [1164] HoA | 2009-01-14 17:47:33 |
 Vagy ugyanez másként: CD szakasz D végpontjában vegyük fel a CD-hez alfa/2 szögben hajló e egyenest. Ezt C középpontú a sugarú körívvel metszve kapjuk B-t. A diszkusszió így talán egyszerűbb: A megadott adatok között milyen összefüggés áll fenn, ha 0, 1 ill. 2 megoldást kapunk?
|
| Előzmény: [1162] jenei.attila, 2009-01-11 13:38:36 |
|
|
| [1162] jenei.attila | 2009-01-11 13:38:36 |
 b-t hosszabítsd meg A csúcson túl c-vel. Az így kapott végpontot jelöld D-vel, vagyis a CD szakasz hossza b+c lesz. Tekintsd a DBA egyenlő szárú háromszöget, amelynek A csúcsba futó szárai c hosszúságúak, a DB alapon fekvő szögei pedig alfa/2 nagyságúak, mivel az A-nál lévő külső szög alfa nagyságú, ami az ABC keresett háromszögünk A-nál lévő adott szöge. A szerkesztés menete: megszerkeszted az a, b+c oldalakkal bíró, alfa/2 nagyságú a-val szemközti szögű háromszöget (a fölé alfa/2 látószögkörív, amit a egyik végpontjából b+c-vel elmetszel; de gondolom ezt nem kell magyarázni). Megkapod, a már említett D pontot. felveszed B-ben a DBA alfa/2 nagyságú szöget. Ahol a szögszár elmetszi a CD szakszat, az lesz az A csúcs. Remélem érthető volt.
|
| Előzmény: [1161] nedijan, 2009-01-11 10:47:13 |
|
| [1161] nedijan | 2009-01-11 10:47:13 |
 Sziasztok!
Lenne egy egyszerű geometriai szerkeztésem, de sehogy nem jövök rá a megoldásra. Adott b+c, a és az a-val szemközti szög. Megszerkezthető-e a háromszög, ha igen adja meg a szerkesztés menetét! Ebben kérem a segítségeteket. Előre is köszönöm.
Jani
|
|
|
|
| [1158] HoA | 2008-12-06 20:33:36 |
 A paraméteres alakot talán úgy a legegyszerűbb felhasználni, hogy AQ és PQ merőlegességét írjuk fel. t-vel paraméterezve AQ = Q - A = ( 4t ; -2t; -3t ) PQ = Q - P = Q - A + A - P = ( Q - A ) - u = ( 4t -6 ; -2t + 4; -3t + 1) . A kettő szorzata 0. 4t ( 4t - 6 ) + 2t ( 2t - 4 ) + 3t ( 3t - 1 ) = 16t2-24t+4t2-8t+9t2-3t=29t2-35t=0 . t-vel oszthatunk - a 0 hosszúságú AA vektor bármire merőleges - , t = 35 / 29 , ami az előző levezetés számszerű eredményét adja.
|
| Előzmény: [1156] BohnerGéza, 2008-12-06 17:47:56 |
|
| [1157] HoA | 2008-12-06 19:00:36 |
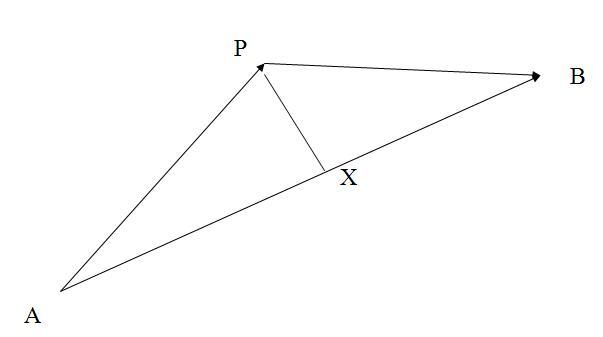
 Ne ijesszük el farkasb-t, nem kell ide szélsőérték-számítás. Az X pont az AB szakaszt az AP szakasz és a PB szakasz AB-re eső vetületeinek arányában osztja. Legyen 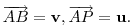 Ekkor Ekkor 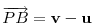 . X = A + m ( B - A ) = m B + ( 1 - m ) A , ahol m és ( 1 - m) aránya az u és a v - u vektor v -re vonatkozó vetületeinek aránya. Innen . X = A + m ( B - A ) = m B + ( 1 - m ) A , ahol m és ( 1 - m) aránya az u és a v - u vektor v -re vonatkozó vetületeinek aránya. Innen
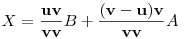
Számadatainkkal u = ( 6;-4;-1 ), v = ( 4;-2;-3 ), v-u = ( -2; 2; -2), uv = 35, (v-u)v = -6, v v = 29.
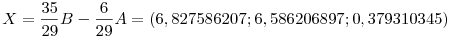 . vegyük észre, hogy az együtthatók összege 1, tehát X valóban az AB egyenes pontja és m > 1, így az ábrával ellentétben X az AB szakasz B-n túli meghosszabbítására esik. . vegyük észre, hogy az együtthatók összege 1, tehát X valóban az AB egyenes pontja és m > 1, így az ábrával ellentétben X az AB szakasz B-n túli meghosszabbítására esik.
|
 |
| Előzmény: [1154] farkasb, 2008-12-05 16:47:37 |
|
|
| [1155] Valezius | 2008-12-06 10:55:08 |
 Az egyenes pontjai ilyen alakúak: (2+4x, 9-2x, 4-3x) P távolsága egy adott ponttól: (8,5,3)-előbbi. Azaz (6+4x, -4-2x, -1-3x) Azt az x-et keressük amire a vektor hossza minimális. A hossza nem más, mint a koordináták négyzetösszege, aminek a szélsőértéke megkapható egy egyszerű deriválással.
|
| Előzmény: [1154] farkasb, 2008-12-05 16:47:37 |
|
| [1154] farkasb | 2008-12-05 16:47:37 |
 Kedves Fórumozók!
Adott A(2,9,4) és B(6,7,1) ponttal meghatározott térbeli egyenes. Adott P(8,5,3) pont. Hogyan számolható ki a P pont vetülete az egynesen? Előre is köszönettel: farkasb
|
|
| [1153] HoA | 2008-11-30 19:48:12 |
 [1150] ábrájának tétele és a 142. feladat egyenértékűek. Jelöljük a D és E közötti piros pontot P-vel. A BE, CE, AD, BD egyenesek által meghatározott négy háromszög közül kettőnek a körülírt köre a P-n és E-n illetve a P-n és D-n áthaladó szaggatott körvonal. P tehát a négy háromszög körülírt köreinek közös pontja, a négy egyenes mint érintők által meghatározott parabola fókusza. A tétel bizonyítása tehát egyben a 142. feladat megoldása is.
Elemi, csak a húrnégyszögek szemközti szögeinek tulajdonságát felhasználó, lépésenként illusztrált bizonyítás található itt: http://agutie.homestead.com/FiLEs/miquel_pentagram1.htm
|
| Előzmény: [1150] BohnerGéza, 2008-11-24 10:16:28 |
|
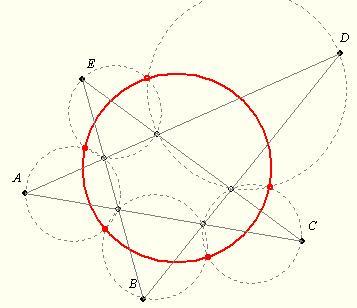
| [1150] BohnerGéza | 2008-11-24 10:16:28 |
 A 138. feladathoz kapcsolódik:
A "Valaki mondja meg!" témában az [573]. hozzászólásban ábra is mutatja a következő tételt:
Ha négy egyenes négy háromszöget alkot, akkor ezek magasságpontjai egy egyenesen vannak, körülírt köreik egy ponton mennek át. Ez a pont és a magasságpontok egyenese parabolát határoz meg, melynek az eredeti 4 egyenes érintője.
Nem ismerek elemi megoldást a következő 142. feladatra:
Bizonyítandó, ha öt egyenes közül bármelyik négy négy háromszöget alkot, akkor az ezekhez a fenti tétel szerint tartozó fókuszok egy körön vannak.
A tétel egy érdekes következménye: Egy konvex ötszög minden +második csúcsát összekötve kapott öt háromszög körülírt köreinek "második" metszéspontjai egy körön vannak. Ábra! Segítségül: http://mathworld.wolfram.com/MiquelsPentagramTheorem.html
|
 |
| Előzmény: [1138] HoA, 2008-10-20 08:50:44 |
|
| [1149] HoA | 2008-11-15 08:07:57 |
 Én viszont teljesen egyetértek BohnerGézával! A [1146] -beli általános leírás és a [1148] -ban kifejtett következtetés együtt teljes mértékben kiváltják a konkrét példára végzett [1147] -beli levezetést. Elnézést kérek, hogy két lépés összevonását nem vettem észre [1146] végén.
|
| Előzmény: [1148] BohnerGéza, 2008-11-15 01:02:26 |
|
| [1148] BohnerGéza | 2008-11-15 01:02:26 |
 Kivételesen nem értek egyet HoA-val, bár ez sem teljesen igaz, csak ezért írom a következőt: Megfogalmazásom túlzottan tömör, komoly végiggondolást igényel, de szerintem teljes.
Az [1146]-ban leírtakból és az [1145]-ben lévő ábrából kiderül, hogy két forgatás szorzata végeredményben két olyan tükrözéssel helyettesíthető, melynek első egyenese az első forgatás kp-ján és az eredményül kapott forgatás kp-ján, a második a második forgatás kp-ján és az eredményül kapott forgatás kp-ján megy át, szögük az eredményforgatás szögének fele.
Kérem mindenkitől, ne adja föl, ha elsőre nem értette, amit írtam! Akarattal teszem, gondolkodást várok! (Ez nem HoA-nak szólt, jogosan figyelmeztetett mostani túlzott tömörségemre.)
|
| Előzmény: [1147] HoA, 2008-11-14 23:02:29 |
|
| [1147] HoA | 2008-11-14 23:02:29 |
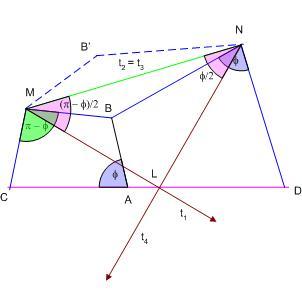
 A leírtak egészen az utolsó mondatig rendben vannak. Ha az utolsó mondatot mint egy itt nem részletezett bizonyítás eredményét tekintjük, akkor az is elfogadható. De önmagában nem. Természetesen ha KM és KN merőlegesek, akkor a rájuk történő tükrözések eredője egy 180 fokos forgatás, vagyis egy K pontra vonatkozó tükrözés. De hát éppen ezt a merőlegességet kéne bizonyítani. A [1146] -ban leírt forgatáshelyettesítésből nem következik, hogy éppen MK és NK lenne az a két egyenes, melyeket t1 -nek és t4 -nek választhatunk. Szerintem a [1146] -beli gondolat feladatunk megoldására az alábbiak szerint használható fel:
Az M körüli  - - szögű forgatás helyettesíthető két, egymással ( szögű forgatás helyettesíthető két, egymással ( - - )/2 szöget bezáró, t1ést2 egyenesre vett tükrözéssel. Válasszuk t2 -nek MN -t, és legyen t1 az ezzel -( )/2 szöget bezáró, t1ést2 egyenesre vett tükrözéssel. Válasszuk t2 -nek MN -t, és legyen t1 az ezzel -( - - )/2 szöget bezáró, M-en áthaladó egyenes. Hasonlóan az N körüli )/2 szöget bezáró, M-en áthaladó egyenes. Hasonlóan az N körüli  szögű forgatás helyettesíthető két, egymással szögű forgatás helyettesíthető két, egymással  /2 szöget bezáró, t3ést4 egyenesre vett tükrözéssel. Válasszuk t3 -nak MN -t, és legyen t4 az ezzel /2 szöget bezáró, t3ést4 egyenesre vett tükrözéssel. Válasszuk t3 -nak MN -t, és legyen t4 az ezzel  /2 szöget bezáró, N-en áthaladó egyenes. Legyen t1 és t4 metszéspontja L. A két forgatás eredője, vagyis a négy tükrözés eredője, mivel a t2 -re és t3 -ra vonatkozó tükrözés eredője azonosság, a t1 -re majd t4 -re végrehajtott tükrözés eredője. /2 szöget bezáró, N-en áthaladó egyenes. Legyen t1 és t4 metszéspontja L. A két forgatás eredője, vagyis a négy tükrözés eredője, mivel a t2 -re és t3 -ra vonatkozó tükrözés eredője azonosság, a t1 -re majd t4 -re végrehajtott tükrözés eredője.
Az MNL háromszögben az M-nél és N-nél lévő szögek összege 90o , ezért a háromszög L-nél derékszögű. Másrészt a tükrözések eredője egy L köröli 180o -os forgatás - L-re vonatkozó tükrözés - és mivel a forgatások eredője C-t D-be viszi, L = K. Ezzel már valóban bizonyítottuk, hogy MK és NK merőlegesek.
|
 |
| Előzmény: [1146] BohnerGéza, 2008-11-11 23:30:46 |
|
|
|
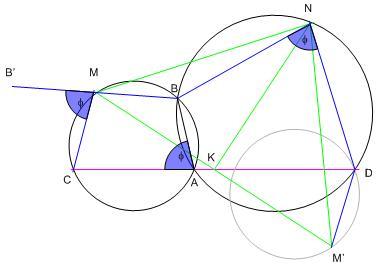
| [1144] HoA | 2008-11-10 11:43:00 |
 A 141.feladat megoldása: Tükrözzük M-et K-ra, a tükörkép legyen M' .
a) Vegyük fel BM meghosszabbításaként az MB' = BM szakaszt. Jelöljük a BND szöget  -vel. ABND és ABMC húrnégyszög, ezért BAC és B'MC szög is -vel. ABND és ABMC húrnégyszög, ezért BAC és B'MC szög is  . Az ívfelezés miatt NB = ND és MB = MC (= MB') , a tükrözés miatt M'D = MC. ND az NB szakasz elforgatottja . Az ívfelezés miatt NB = ND és MB = MC (= MB') , a tükrözés miatt M'D = MC. ND az NB szakasz elforgatottja  -vel, a DM' -vel egyállású MC a BM -mel egyállású MB' elforgatottja -vel, a DM' -vel egyállású MC a BM -mel egyállású MB' elforgatottja  -vel, ezért NBM és NDM' háromszögek egybevágóak, NM = NM' . NK az MM'N egyenlőszárú háromszög alaphoz tartozó súlyvonala, tehát NK merőleges MK-ra. -vel, ezért NBM és NDM' háromszögek egybevágóak, NM = NM' . NK az MM'N egyenlőszárú háromszög alaphoz tartozó súlyvonala, tehát NK merőleges MK-ra.
b) Felhasználjuk, hogy egy X pont körüli  szögű és egy Y pont körüli szögű és egy Y pont körüli  szögű elforgatás eredője egy Z pont körüli szögű elforgatás eredője egy Z pont körüli  + + szögű elforgatás, speciálisan ha szögű elforgatás, speciálisan ha  + + = = , akkor egy Z pontra vonatkozó tükrözés. CMB szög = , akkor egy Z pontra vonatkozó tükrözés. CMB szög =  - - , az M körüli , az M körüli  - - szögű elforgatás C-t B-be viszi, az N körüli szögű elforgatás C-t B-be viszi, az N körüli  szögű elforgatás B-t D-be viszi, a két elforgatás eredője C-t D-be viszi. Mivel a két elforgatás eredője egy pontra vonatkozó tükrözés, ez a pont éppen K, tehát a két forgatás eredője egy K-ra vett tükrözés. Alkalmazzuk a két elforgatást M-re. Az M körüli forgatás M-et helyben hagyja, az N körüli forgatás egy olyan M' pontba viszi, melyre NM = NM' . Ugyanakkor M' éppen az M pont K-ra vett tükörképe. NK az MM'N egyenlőszárú háromszög alaphoz tartozó súlyvonala, tehát NK merőleges MK-ra. szögű elforgatás B-t D-be viszi, a két elforgatás eredője C-t D-be viszi. Mivel a két elforgatás eredője egy pontra vonatkozó tükrözés, ez a pont éppen K, tehát a két forgatás eredője egy K-ra vett tükrözés. Alkalmazzuk a két elforgatást M-re. Az M körüli forgatás M-et helyben hagyja, az N körüli forgatás egy olyan M' pontba viszi, melyre NM = NM' . Ugyanakkor M' éppen az M pont K-ra vett tükörképe. NK az MM'N egyenlőszárú háromszög alaphoz tartozó súlyvonala, tehát NK merőleges MK-ra.
|
 |
| Előzmény: [1143] BohnerGéza, 2008-11-05 23:18:14 |
|
| [1143] BohnerGéza | 2008-11-05 23:18:14 |
 A "kis segítség" önnálló feladatnak biztosan jó, ajánlom mindenkinek!
A 141. feladatra két megoldást ismerek, azokhoz nem használtuk ezt a segítséget, talán egy harmadikhoz jó.
Az általam ismett megodások alapszava:
- - - egyikhez: "ha felező..., akkor tükrözzünk rá!"
- - - másikhoz: "leképezések"
|
| Előzmény: [1142] HoA, 2008-11-05 11:24:39 |
|










 -
- szögű forgatás helyettesíthető két, egymással (
szögű forgatás helyettesíthető két, egymással (

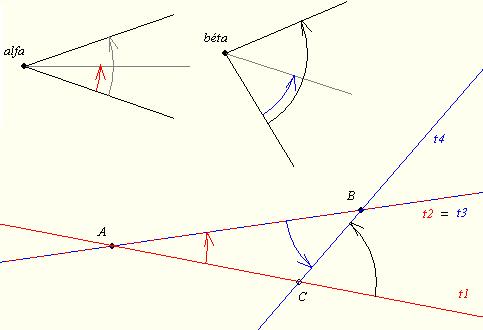
 szögű és egy Y pont körüli
szögű és egy Y pont körüli  szögű elforgatás eredője egy Z pont körüli
szögű elforgatás eredője egy Z pont körüli 