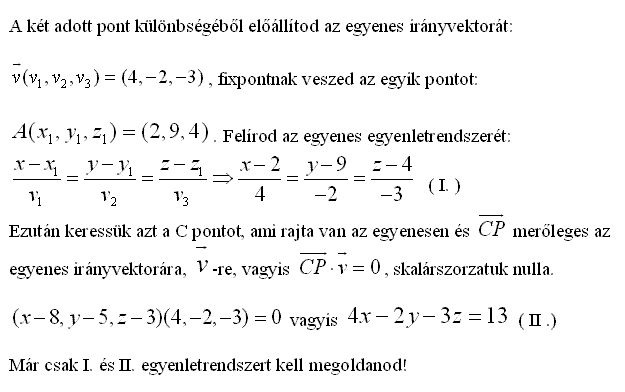| [1194] BohnerGéza | 2009-03-31 20:48:12 |
 A Surányi János emlékverseny 2. feladata alapján.
147. feladat: Érintse a k kör az AB egyenest az A pontban és legyen C a k egy A-tól különböző pontja, F az AB szakasz felezőpontja. Az FC messe még k-t az I pontban, az A-nak a BI-re eső merőleges vetülete D.
Bizonyítandó, hogy CF felezi a DFB szöget.
|
|
| [1193] HoA | 2009-03-28 14:32:44 |
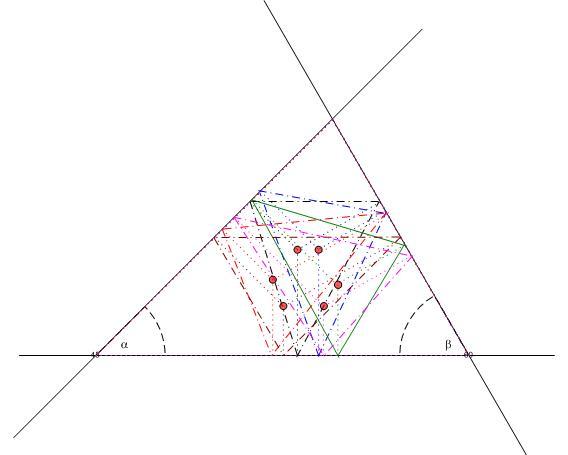
 144.b feladathoz: Az ABC háromszögön belüli P pontokra a talpponti DEF háromszögben a megfelelő pontok hat különböző helyzetben lehetnek szabálytalan hegyesszögű háromszög esetén, lásd [1190] ábráját. A [1189]-ben vázolt szerkesztést elvégezve mind a hat pontra kapunk megoldást az ábra szerint.
|
 |
| Előzmény: [1192] BohnerGéza, 2009-03-25 04:35:44 |
|
| [1192] BohnerGéza | 2009-03-25 04:35:44 |
 a 144. feladattal kapcsolatban:
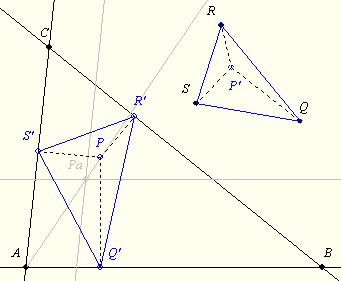
HoA nagy ötlete után példát mutatok az adott ABC háromszöghöz olyan P pont szerkesztésére, amelyhez adott QRS háromszöghöz hasonló talpháromszög tartozik:
Az ábra Q’PS’ szöge 180 fok-alfa, egyenlő a QP’S szöggel, így P’ számára adott vonal a QS szakasz 180 fok-alfa szögű látóköre. Hasonlóan pl. az RQ 180 fok-béta látóköre is, így P’ szerkeszthető.
A Pa pont SP’ távolságra van az AC-től és QP’-re az AB-től. P-nek az APa-n (és hasonlóan a BPb-n) kell lenni. …
Természetesen több megoldása lehet (van) a feladatnak. 144.b feladat: Adjuk meg a lehetséges megoldások számát!
|
 |
| Előzmény: [1188] HoA, 2009-03-22 19:52:41 |
|
| [1191] Maga Péter | 2009-03-22 22:33:02 |
 Szia! - 2 hónap késéssel, de...
Látom, hogy már kaptál segítséget, de ha dobsz egy e-mailt, akkor tudok küldeni egy anyagot. Nem egészen elemi, de annak idején (tavaly vagy tavalyelőtt) a debreceni Fazekas Gimnázium matek önképzőkörén mondtam el, és értették, legalábbis úgy tettek:).
|
| Előzmény: [1166] edu, 2009-01-23 09:22:12 |
|
|
|
| [1188] HoA | 2009-03-22 19:52:41 |
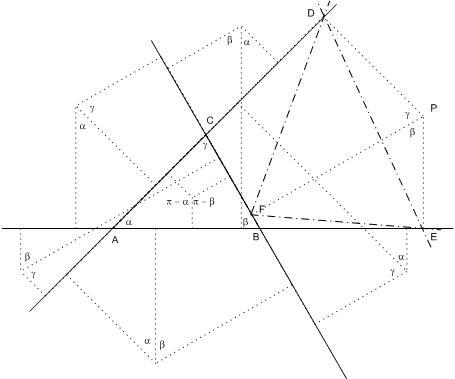
 Nevezzük a megfelelő P pont vetületei által meghatározott háromszöget P talpponti háromszögének. Mit állapíthatunk meg az adott ABC háromszög oldalegyenesei által hét tartományra osztott sík egyes részeiben a P-ből a talpponti háromszög csúcsaiba vezető szakaszok által bezárt szögekről? Az 1. ábráról leolvasható, hogy 2-2 tartományban ezek a szakaszok egymással nem egymás szögtartományába eső , szokásos szögmérési irányban mért (  , , ) , ( ) , (  , , ) illetve ( ) illetve (  , , ) szögeket zárnak be. A háromszög belsejében a megfelelő szakaszok szöge pl. ( ) szögeket zárnak be. A háromszög belsejében a megfelelő szakaszok szöge pl. (  – – , , – – ) )
A keresendő P pontok lehetséges helyzetét vizsgáljuk nem az ABC, hanem a talpponti, DEF háromszöghöz képest. Ezzel a keresett P pontok megszerkesztésének egy lehetséges útját is kijelöljük. Általános hegyesszögű ( 45, 60 75 fokos ) háromszöget választottam. ( Majd meg kell vizsgálni, hogy módosulnak az eredmények egyenlőszárú, egyenlőoldalú, derékszögű, tompaszögű, vagy akár más általános hegyesszögű háromszög esetében. ) Ha van megfelelő P pont az 1. ábra BC szakaszának A-t nem tartalmazó oldalán lévő síktartományban, akkor P-ből a DEF háromszög egy-egy oldala  ill. ill.  szög alatt látszik, mégpedig úgy, hogy P DEF egy-egy oldalának szög alatt látszik, mégpedig úgy, hogy P DEF egy-egy oldalának  ill. ill.  látószögű, a háromszög belseje felé eső körívén van. ( Mikor jöhetnek szóba a külső körívek? ) látószögű, a háromszög belseje felé eső körívén van. ( Mikor jöhetnek szóba a külső körívek? )
|
 |
| Előzmény: [1186] BohnerGéza, 2009-03-19 19:55:52 |
|
| [1187] fityfiritty | 2009-03-21 20:17:29 |
 Köszönöm.
Itt egy új, a számozottak között 146. feladat:
A hegyesszögű APD AP, illetve PD oldalának tetszőleges pontja rendre B, illetve C. Az ABCD négyszög átlói a Q pontban metszik egymást. M1, illetve M2 rendre az APD AP, illetve PD oldalának tetszőleges pontja rendre B, illetve C. Az ABCD négyszög átlói a Q pontban metszik egymást. M1, illetve M2 rendre az APD , illetve a BPC , illetve a BPC magasságpontja. Az ABQ és CDQ háromszögek körülírt köreinek Q-tól különböző metszéspontja legyen X, a BCQ és ADQ háromszögekre ugyanígy kapott pont pedig legyen Y. Bizonyítsuk be, hogy: ha az M1, M2 és X pontok egy e egyenesre esnek, akkor Y magasságpontja. Az ABQ és CDQ háromszögek körülírt köreinek Q-tól különböző metszéspontja legyen X, a BCQ és ADQ háromszögekre ugyanígy kapott pont pedig legyen Y. Bizonyítsuk be, hogy: ha az M1, M2 és X pontok egy e egyenesre esnek, akkor Y  e. e.
|
| Előzmény: [1182] HoA, 2009-03-16 16:59:04 |
|
| [1186] BohnerGéza | 2009-03-19 19:55:52 |
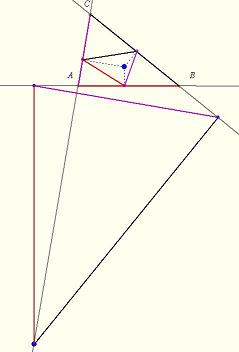
 A 144. feladathoz: Az ábrán látható két olyan (a két kék ponthoz tartozó) az eredetihez hasonló "talpháromszög", melyekben az AB-nek megfelelő oldal az AB és az AC egyenest köti össze.
Az előző hozzászólás ábráján is két ilyen van, a zöld és a barna ponthoz tartozó. ...?
|
 |
| Előzmény: [1185] BohnerGéza, 2009-03-19 17:53:44 |
|
| [1185] BohnerGéza | 2009-03-19 17:53:44 |
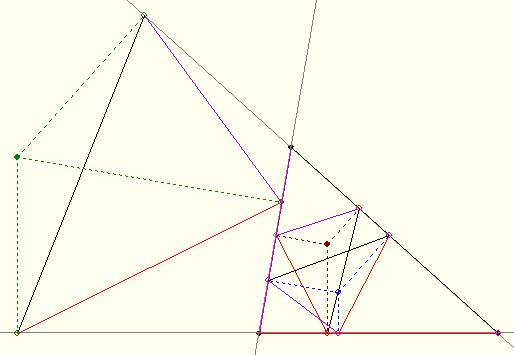
 A 144. feladathoz: Az ábrán látható három, az eredetihez hasonló "talpháromszög".
A barna és a kék pont a háromszög Brocard-pontja. Azt nem nagyon nehéz bizonyítani, hogy a hozzájuk tartozó talpháromszögek megfelelnek a feladatnak, hogy ez a kettő egybevágó azt nehezebb.
A körülírt kör kp-jához tartozó középvonali háromszög is jó.
Az ábra zöld pontja is jó. ...?
|
 |
| Előzmény: [1173] BohnerGéza, 2009-02-16 20:08:53 |
|
|
| [1183] SmallPotato | 2009-03-17 22:57:39 |
 Találtam egy olyan irodalmat, amelyik talán érthetően vezeti le a dolgot. A 60-61. oldalakon van a Téged érintő/érdeklő rész. Ott y,x1,x2 változókról beszél, ezek a Te példádban (sorrendben) z,x,y.
A mintafeladatodat megcsináltam ezeknek az egyenleteknek a segítségével (a 61. oldal tetején a három egyenlet - mint egyenletrendszer - megoldása), és Excelben is (LIN.ILL függvény). Az eredmények teljesen megegyeznek.
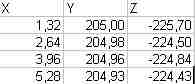
A regressziós sík egyenlete a kis példádra, 6 értékes jegyre:
z=0,744949x+27,6667y-5898,09
Írj mailt, megküldöm az Excel-táblát.
|
| Előzmény: [1181] david20, 2009-03-16 12:01:19 |
|
|
| [1181] david20 | 2009-03-16 12:01:19 |
 Üdvözöllek!
Elolvastam a linkelt doksikat, és sok példát is találtam a neten, de valahogy nem akar kijönni...
Tudna valaki egy kis példán keresztül segíteni a "regressziós sík" kiszámításában az alábbi pontokra.
Előre is köszönöm.
|
 |
| Előzmény: [1177] SmallPotato, 2009-03-11 01:09:43 |
|
|
| [1179] Gábor1905 | 2009-03-11 22:54:12 |
 Üdv. A következő kérdésre szeretnék választ kapni: Van-e olyan konvex 5, vagy attól többszög, aminek több mint 4 belső szöge 120°, vagy attól kisebb. Minden ötlet nagyon érdekel! Előre is köszönöm.
|
|
|
| [1177] SmallPotato | 2009-03-11 01:09:43 |
 Hogy a pontok mennyire pontosan vannak egy körvonalon, az - szerintem - gyakorlatilag mindegy. Ami nem mindegy: hogy egy síkban vannak-e. Ha nincsenek, akkor regressziós síkot kell keresni. (Ellenkező esetben nyilván bármelyik 3 pont kifeszíti a keresett síkot.) Regressziós sík megtalálására az irodalomban (pl. itt) találsz több megközelítést is (kiemelés tőlem):
"... egy, a megadott pontokhoz leginkább simuló általános kiegyenlítő sík egyenletét határozza meg, úgy, hogy a pontok és a sík közötti z irányú távolságok négyzetösszegét minimalizálja ..."
vagy
"... a megadott pontokhoz legjobban simuló kiegyenlítő sík egyenletét számítja ki úgy, hogy a pontok és a sík közötti merőleges távolságok négyzetösszegét minimalizálja ..."
Amit még találtam hirtelen: A regressziószámítás gyakorlati kérdései
Ha a regressziós egyenes megkeresésének módját ismered (így van vajon?), nem sok gondod lesz a síkkal sem.
|
| Előzmény: [1176] david20, 2009-03-10 13:12:11 |
|
| [1176] david20 | 2009-03-10 13:12:11 |
 Üdvözlök Mindenkit!
Egy kis segítségre lenne szükségem.
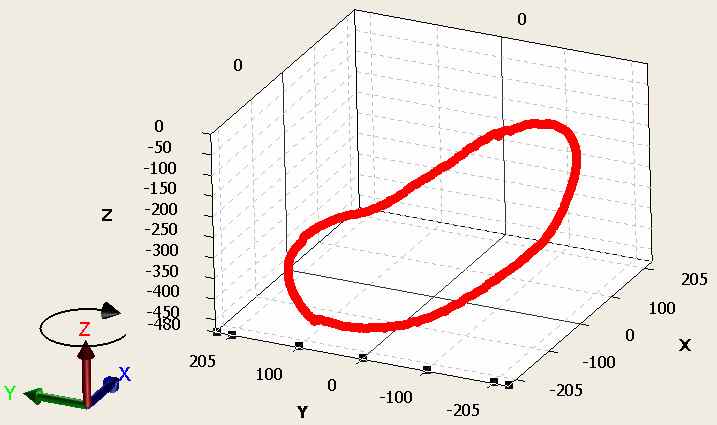
Adott egy térbeli koordináta rendszer, és 600 pont (X,Y,X), amik megközelítőleg (nem pontosan) egy kör körvonalán helyezkednek el. A kör síkja nem párhuzamos az XY síkkal.
A pontok a koordináta rendszerben való ábrázolása a képen látható.
Hogyan lehetne ezekre a pontokra egy síkot illeszteni?
Minden segítséget nagyon szépen köszönök.
David20
david20x@gmail.com
|
 |
|
|
|
| [1173] BohnerGéza | 2009-02-16 20:08:53 |
 144. feladat: Adott háromszög esetén határozzuk meg azon pontok halmazát, melyeknek a három oldalegyenesre eső merőleges vetülete az eredetihez hasonló háromszöget határoz meg.
|
|
| [1172] BohnerGéza | 2009-02-05 23:48:17 |
 HoA szép megoldása - az (1) tétel ismerete - után már könnyebb a következő feladat!
143/2. feladat: Bizonyítandó, hogy egy nem derékszögű háromszögnek és a magasságpontja oldalfelezőpontokra vonatkozó tükörképei által kapott háromszögnek ugyanazon ponthoz tartozó Simson-egyenese merőleges egymásra!
|
| Előzmény: [1170] HoA, 2009-02-05 20:03:36 |
|
|
| [1170] HoA | 2009-02-05 20:03:36 |
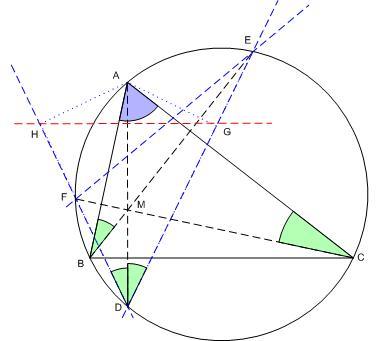
 Azért nem várok egy hetet, mert az alábbi megoldás nem csak a középiskolai anyagra támaszkodik, kihasználja a Simson egyenesnek azt a tulajdonságát, hogy
a körülírt kör két , P és Q pontjához tartozó Simson egyenes szöge megegyezik a körülírt kör PQ ívéhez tartozó középponti szög felével. (1)
Ennek alapján elég az állítást a körülírt kör tetszőleges P pontjára belátni, hiszen P-t bármely más pontba mozgatva a két vizsgált háromszögre vonatkozó Simson egyenes ugyanazzal a szöggel fordul el, tehát megtartják merőlegességüket. Legyen az ABC háromszög magasságpontja M, az AM, BM, CM magasságoknak a körülírt körrel alkotott másik metszéspontjuk rendre D,E,F. ACF és EBA szögek egyenlőek, mert egy  szögű derékszögű háromszög harmadik szögei. Ezért az AE és AF ívek egyenlőek, és a hozzájuk tartozó EDA és ADF kerületi szögek is. Legyen P = A. Ekkor az ABC háromszögre vonatkozó Simson egyenes az AD magasságvonal. A-ból ED-re és FD-re bocsátott merőleges talppontja G és H. ADG és ADH egybevágó derékszögű háromszögek, G és H egymás tükörképei AD-re, ezért GH, az A pont EFG háromszögre vonatkozó Simson egyenese merőleges AD-re. szögű derékszögű háromszög harmadik szögei. Ezért az AE és AF ívek egyenlőek, és a hozzájuk tartozó EDA és ADF kerületi szögek is. Legyen P = A. Ekkor az ABC háromszögre vonatkozó Simson egyenes az AD magasságvonal. A-ból ED-re és FD-re bocsátott merőleges talppontja G és H. ADG és ADH egybevágó derékszögű háromszögek, G és H egymás tükörképei AD-re, ezért GH, az A pont EFG háromszögre vonatkozó Simson egyenese merőleges AD-re.
Talán tud valaki közvetlen, az (1) tételt nem felhasználó megoldást.
|
 |
| Előzmény: [1169] BohnerGéza, 2009-02-04 14:46:10 |
|







 -
- ill.
ill.  szög alatt látszik. A 3. ábrán ezért a DEF háromszög oldalainak
szög alatt látszik. A 3. ábrán ezért a DEF háromszög oldalainak  (lila) látószögű köríveket is, ezek természetesen áthaladnak ugyanazokon a metszéspontokon. A hat metszéspont közül az egyik DEF magasságpontja. Tudjuk, ez felel meg annak, ha P gyanánt ABC körülírt körének középpontját választjuk. Két másik metszéspont DEF első ill. második Brocard pontja (Könnyen belátható, hogy a Brocard pontokból két oldal látószöge
(lila) látószögű köríveket is, ezek természetesen áthaladnak ugyanazokon a metszéspontokon. A hat metszéspont közül az egyik DEF magasságpontja. Tudjuk, ez felel meg annak, ha P gyanánt ABC körülírt körének középpontját választjuk. Két másik metszéspont DEF első ill. második Brocard pontja (Könnyen belátható, hogy a Brocard pontokból két oldal látószöge 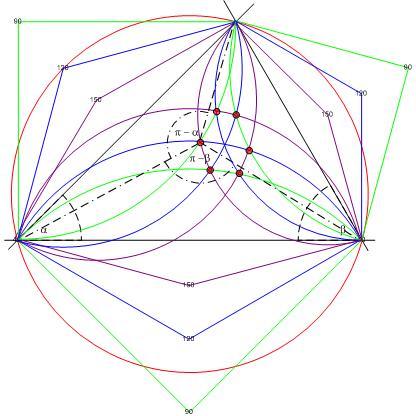
 . Vegyük fel az 1. ábrán az AC szakasz C-n túli meghosszabbításán a D’ pontot. A D’-pontban AC-re emelt merőlegessel annak A-t tartalmazó oldalán
. Vegyük fel az 1. ábrán az AC szakasz C-n túli meghosszabbításán a D’ pontot. A D’-pontban AC-re emelt merőlegessel annak A-t tartalmazó oldalán 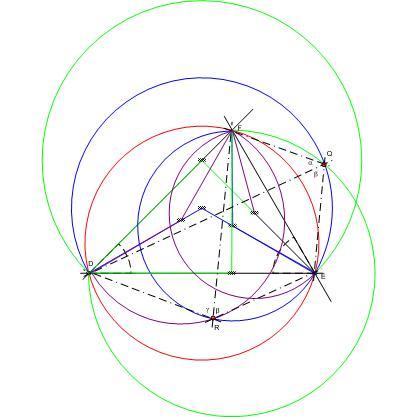


 AP, illetve PD oldalának tetszőleges pontja rendre B, illetve C. Az ABCD négyszög átlói a Q pontban metszik egymást. M1, illetve M2 rendre az APD
AP, illetve PD oldalának tetszőleges pontja rendre B, illetve C. Az ABCD négyszög átlói a Q pontban metszik egymást. M1, illetve M2 rendre az APD e.
e.