| [1219] HoA | 2009-05-14 15:22:08 |
 Szia Kandi! Ez itt a KöMaL Geometria fóruma. Feladataid úgy látom, nem egészen a középiskolai geometria témájába tartoznak, ami még önmagában nem baj. Csak az nem világos, miről is van szó. A használt fogalmak alapján úgy gondolom, valamilyen projektív geometriai kurzusra jársz. A feladatok esetleg mind centrális kollineáció témába esnek? Ha nem ismered, talán segít ez a jegyzet:
http://www.jgytf.u-szeged.hu/~krisztin/projektiv.doc
|
| Előzmény: [1218] kandi, 2009-05-13 07:55:44 |
|
| [1218] kandi | 2009-05-13 07:55:44 |
 Szia Mindenki! Én még itt új vagyok, úgyhogy nem nagyon tudom, hogy hogyan működik, de nagy segítségre lenne szükségem. Van 5 db szerkesztési példám. Ami elvileg nagyon könnyű, de én nem tudtam megcsinálni, ha valaki segítene megköszönném. Leírom a feladatokat: 1., adott : tengely, centrum, eltűnési egyenes.Szerk. meg tetszőleges pont képét! 2., adott : tengely, centrum, ideális egyenes képe.Szerk. meg tetszőleges pont képét! 3., adott : az eltűnési egyenes, az ideális egyenes képe, és egy egymásnak megfelelő egyenespár.Szerk. meg a centrumot és a tengelyt! 4., adott : egy megfelelő pontpár, egy megfelelő egyenespár és a tengely egy pontja. Szerk. meg a centrumot és a tengelyt! 5., adott : a centrum és egy megfelelő pontpár. Határozzuk meg a tengelyt úgy, hogy egy előre adott ABCD négyszög képe paralelogramma legyen! Előre is köszönöm:)
|
|
| [1217] MTM | 2009-05-12 18:06:51 |
 151.feladat:
ABC háromszög körülírt körét, AB és AC oldalt rendre D, E, G-ben érinti egy kör. Bizonyítsuk be, hogy BDC szög felezője felezi EG szakaszt.
|
|
|
|
|
| [1213] sakkmath | 2009-05-12 15:20:18 |
 A HoA [1208]-as hozzászólásában kitűzött 150. feladat két feladatnak tekinthető. Elnézést, de sajnos csak négy részletben tudom feltenni a megoldást: a képek 50 KB-os határával a megfelelő képminőség ugyanis nem összeegyeztethető.
A megoldás 1. része:
|
 |
| Előzmény: [1208] HoA, 2009-04-29 15:00:17 |
|
|
| [1211] BohnerGéza | 2009-05-11 23:22:32 |
 Segítség a 150. feladat egy lehetséges megoldásához: Az E és D pontot máshogy definiálva lássuk be addíciós tételek következménye segítségével, hogy megfelelnek az eredeti definíciónak.
Egyelőre megpróbálok más jellegű (számomra szebb) megoldást is kitalálni.
|
| Előzmény: [1208] HoA, 2009-04-29 15:00:17 |
|
| [1210] HoA | 2009-05-07 22:43:48 |
 Mit néztél el? Szerintem a feladat jó. Nyilván sokunknak beugrik a hetedik, azonos sugarú kört és egymást érintő hat kör, és ezek befoglaló köre. De azt nem sikerült bizonyítanom, hogy a hetedik kör elhagyásával nem adható jobb megoldás - kisebb befoglaló kör.
|
| Előzmény: [1209] BohnerGéza, 2009-05-07 00:35:55 |
|
|
|
| [1207] BohnerGéza | 2009-04-17 13:56:24 |
 A 149. feladathoz: 2. rész.
Az előző [1206] hozzászólás folytatása.
A megoldásban nem törekedtem a teljességre, a legegyszerűbb megfogalmazásra, inkább a gondolatmenet bemutatására.
Jó lenne, ha valaki szebben megfogalmazott, vagy más jellegű megoldást is adna!
Vegyük észre a kapcsolatot az itt és HoA[1204] hozzászólásában látottak közt!
|
 |
| Előzmény: [1206] BohnerGéza, 2009-04-17 13:43:59 |
|
| [1206] BohnerGéza | 2009-04-17 13:43:59 |
 A 149. feladathoz: 1. rész.
Folytatása a következő hozzászólásban.
|
 |
|
| [1205] BohnerGéza | 2009-04-17 13:29:51 |
 Nekem is hiányérzetem volt janomo[1200] hozzászólásával kapcsolatban. Igaz így legalább HoA pontos, érthető megfogalmazásában láthattuk a megoldást!
Példát mutatok egy kevésbé szépre a következő hozzászólásban, az eredeti feladat kapcsán. Remélem, látható lesz belőle, hogy a szép megoldások is esetleg hosszabb gondolkodás után, sok munka árán, nem véletlenszerűen jönnek össze. Az így elért eredmény, sőt részeredmény is örömet adhat. (Ráadásul nem kell közben pl. négykerekű motoros marhasággal -nem jut eszembe a neve - tönkretenni a környezetet.)
149. feladat: A Surányi János emlékverseny 2. feladata: Az ABC háromszög beírt köre az AB és AC oldalakat rendre a D és E pontban érinti. A beírt körnek és az AEB háromszög köré írt körnek E-től különböző közös pontja legyen F, a D pont merőleges vetülete az EB egyenesen G. Igazoljuk, hogy 2ABEszög=BFGszög.
(Elnézést, a továbbiakban ezeket az eredeti jelöléseket használom!)
|
| Előzmény: [1204] HoA, 2009-04-17 09:10:46 |
|
| [1204] HoA | 2009-04-17 09:10:46 |
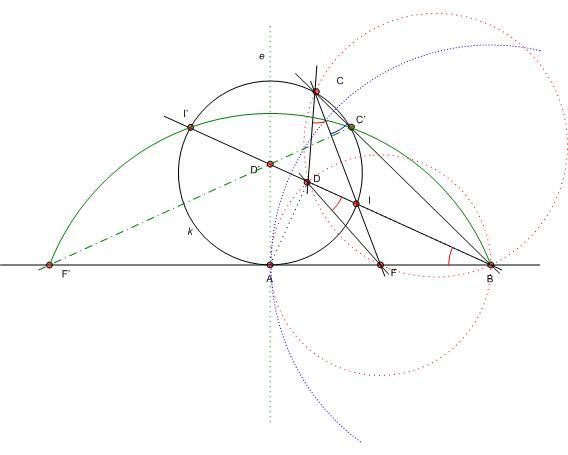
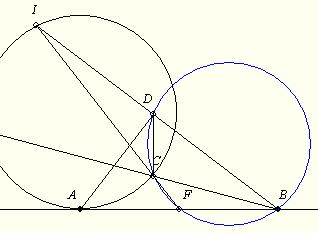
 Szerintem nem érdemes annyival elintézni az inverziós megoldást, hogy „inverzió a B pontra és kész”. Más feladatoknál is felhasználható például, hogy három, a póluson nem áthaladó egyenesen fekvő pont képe egy, a póluson átmenő körön van, és viszont: ha négy pont húrnégyszöget alkot – egy körön van – akkor egyiküket pólusnak választva a másik három pont inverz képe egy egyenesen fekszik.
Legyen tehát az inverzió pólusa B, alapköre a k-t merőlegesen metsző kör. Ekkor k képe önmaga, A és A’ egybeesik, F képe az AB egyenes F’ pontja, melyre F’A = AB, AB Thálesz-körének képe az AB-re merőleges e egyenes, D képe, D’ BD és e metszéspontja, I képe a BI egyenes k-val alkotott második metszéspontja. CIF egyenes képe a B’, F’, I’ pontok által meghatározott kör. Ennek F’B húrja, e húrfelező merőlegese, tehát szimmetriatengelye. e k-nak is szimmetriatengelye, így a két kör metszéspontjai, C’ és I’ egymás tükörképei e-re. Ez igaz az F’, B pontpárra is, tehát a BD’I’ egyenes e-re vett tükörképe az F’D’C’ egyenes. A fentiek szerint ezért BCDF húrnégyszög, körülírt körében az egyenlő BF és DF húrokhoz egyenlő kerületi szögek tartoznak: DCF =FCB =FCB . .
|
 |
| Előzmény: [1200] janomo, 2009-04-04 12:18:33 |
|
| [1203] BohnerGéza | 2009-04-08 05:14:08 |
 148. feladat: Mekkora annak a legkisebb körnek a sugara, amelyben átfedés nélkül elfér 6 db 4 cm sugarú kör? (Érintkezés lehet.)
|
|
|
|
|
|
|
| [1197] BohnerGéza | 2009-04-01 19:15:28 |
 Köszönöm HoA! Elírtam. Helyesen a feladat:
A Surányi János emlékverseny 2. feladata alapján.
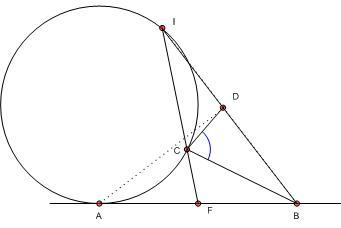
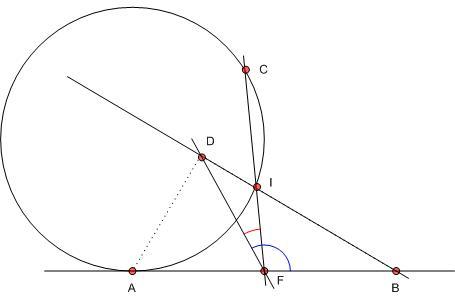
147. feladat: Érintse a k kör az AB egyenest az A pontban és legyen C a k egy A-tól különböző pontja, F az AB szakasz felezőpontja. Az FC messe még k-t az I pontban, az A-nak a BI-re eső merőleges vetülete D.
Bizonyítandó, hogy CF felezi a DCB szöget.
|
| Előzmény: [1196] HoA, 2009-04-01 16:15:55 |
|
|
| [1195] BohnerGéza | 2009-03-31 20:57:04 |
 Örülnék, ha nem csak HoA kapcsolódna be a 144. és 144.b feladat megoldásába.
Hogy jellemezhető pl. HoA 6 megoldása, hány és milyen megoldást adó P lehet még a háromszögön kívül?
|
| Előzmény: [1193] HoA, 2009-03-28 14:32:44 |
|





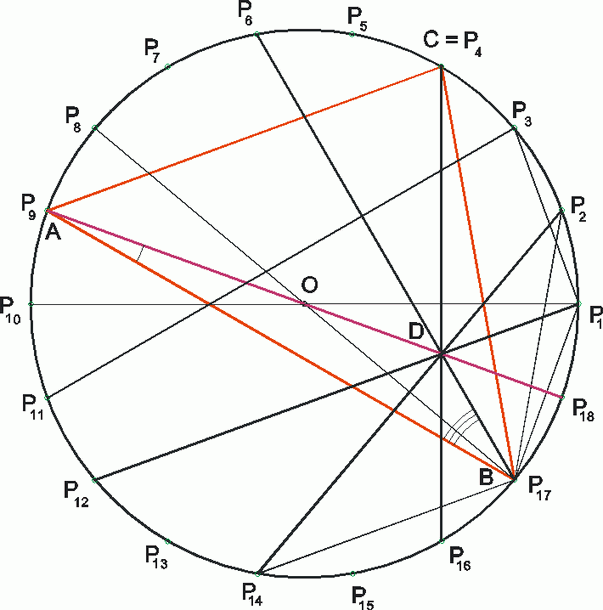



 =EAB
=EAB


 -ek hasonlók, FBD
-ek hasonlók, FBD