| [1244] HoA | 2009-08-10 23:29:05 |
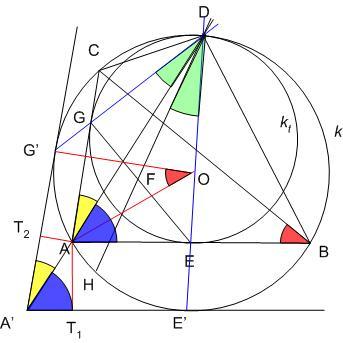
 A 151. feladathoz: Legyen a körülírt kör k, a D, E, G pontokon átmenő kör kt . D a két kör hasonlósági pontja . Ebben a hasonlóságban E, A, G megfelelője rendre E’, A’, G’ . E’A’ párhuzamos az EA egyenessel és E’-ben érinti k-t, ezért E’ az AB ív felezőpontja, E’DA’ =EDA =EDA = = /2 . Hasonlóan G’ az AC ív felezőpontja, G’DA’ /2 . Hasonlóan G’ az AC ív felezőpontja, G’DA’ =GDA =GDA = = /2. Ossza a DA egyenes ABC /2. Ossza a DA egyenes ABC  szögét BAD= szögét BAD= 1 és DAC= 1 és DAC= 2 szögekre. AG és A’G’ egyenesek távolsága AT2=r(1–cos 2 szögekre. AG és A’G’ egyenesek távolsága AT2=r(1–cos )=AA’sin )=AA’sin 2 , hasonlóan AT1=r(1–cos 2 , hasonlóan AT1=r(1–cos )=AA’sin )=AA’sin 1 . Innen 1 . Innen
 | (1) |
AG = AE = t jelöléssel az ADG ben t.sin ben t.sin 2=DGsin 2=DGsin /2 , DG=t.sin /2 , DG=t.sin 2/sin 2/sin /2 . AED /2 . AED ben ugyanígy DE=t.sin ben ugyanígy DE=t.sin 1/sin 1/sin /2 . BDC szög felezője messe GE-t F-ben, k-t H-ban. A felezés miatt HDE’=FDE /2 . BDC szög felezője messe GE-t F-ben, k-t H-ban. A felezés miatt HDE’=FDE = = /2 és HDG’=FDG /2 és HDG’=FDG = = /2 . DEF és DFG /2 . DEF és DFG  -ek kétszeres területére : -ek kétszeres területére :
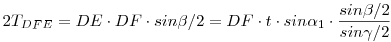
,
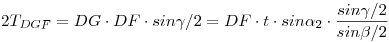
A területek aránya (1) miatt 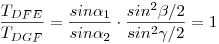 . A két . A két  közös oldalegyenese GE, közös magasságuk a D-ből erre bocsátott merőleges, területük egyenlőségéből következik, hogy GF = FE. közös oldalegyenese GE, közös magasságuk a D-ből erre bocsátott merőleges, területük egyenlőségéből következik, hogy GF = FE.
151/2 feladat: Bizonyítsuk be, hogy F az ABC beírt körének középpontja beírt körének középpontja
|
 |
| Előzmény: [1217] MTM, 2009-05-12 18:06:51 |
|
|
| [1242] BohnerGéza | 2009-08-05 14:28:22 |
 Már picit gondolkodva is, nem csak szerkesztőprogrammal játszva:
Ha a nagy gamma (KLM) kör érinti a PQ-t, akkor azt az M felezőpontban teszi. Ekkor a KLM-kör R kp-ja egyenlő távol van P-től és Q-tól. Ha a feladat állítása igaz, M, R és O egy egyenesen van.
Ha ez mindig igaz, abból következik a feladat állítása.
Bizonyítsuk, hogy M, R és O egy egyenesen van!
|
| Előzmény: [1239] Fálesz Mihály, 2009-07-18 06:28:32 |
|
| [1241] HoA | 2009-08-05 08:09:20 |
 A 151. feladathoz: Szerkesztőprogrammal nézegetve úgy tűnik, hogy az EG szakasz F felezőpontja ABC háromszög beírt körének középpontja. Talán segít, ha először ezt bizonyítjuk.
|
| Előzmény: [1217] MTM, 2009-05-12 18:06:51 |
|
|
| [1239] Fálesz Mihály | 2009-07-18 06:28:32 |
 153. feladat (az idei matematikai diákolimpia 2. feladata).
Az ABC háromszög köré írt kör középpontja O. P és Q belső pontjai a CA, illetve AB oldalaknak. Legyen K, L és M a BP, CQ, illetve PQ szakaszok felezőpontja, és legyen  a K,L,M pontokon átmenő kör. Bizonyítsuk be, hogy ha a K,L,M pontokon átmenő kör. Bizonyítsuk be, hogy ha  érinti a PQ egyenest, akkor OP=OQ. érinti a PQ egyenest, akkor OP=OQ.
|
|
|
| [1237] sakkmath | 2009-06-15 15:54:30 |
 Hasznos volt egy kicsit kibontani a megoldás menetét, több szempontból is. Nekem például ezzel vált világossá, hogy valóban kulcsszerep jut az M pontnak. Melyről most már elárulhatjuk: ez a Miquel-pont, amely nemrég több itteni hozzászólás témája volt.
Múlik az idő, úgy tűnik, ideje feltenni a 152. feladatra egy olyan megoldást, amely a [1232]-ben közölt megoldásod a) megjegyzésére válaszol. Az ugyanitt javasolt 152/3. feladatra még megoldó kerestetik... . Később egyébként megnevezem a feladat elődjét, a megoldás elérhetőségét is megadva.
Következzék tehát a [1230]/152. példa egy újabb megoldása. Az 1. rész:
|
 |
| Előzmény: [1236] HoA, 2009-06-08 11:50:35 |
|
| [1236] HoA | 2009-06-08 11:50:35 |
 A leírtakkal egyetértek, sőt nagy részét evidensnek tartom. Megjegyzésem nem kívánt a kitűzés kritikája lenni. Ha már úgyis egy kicsit OFF vagyunk, leírom, hogyan jöttem rá én a megoldásra. Egyrészt hogy bemutassam, milyen értelemben „válik az M pont a megoldás kulcsává”, másrészt mert egy matematika oktatáshoz kapcsolódó fórumon talán nem baj, ha időnként ilyesmit is leírunk.
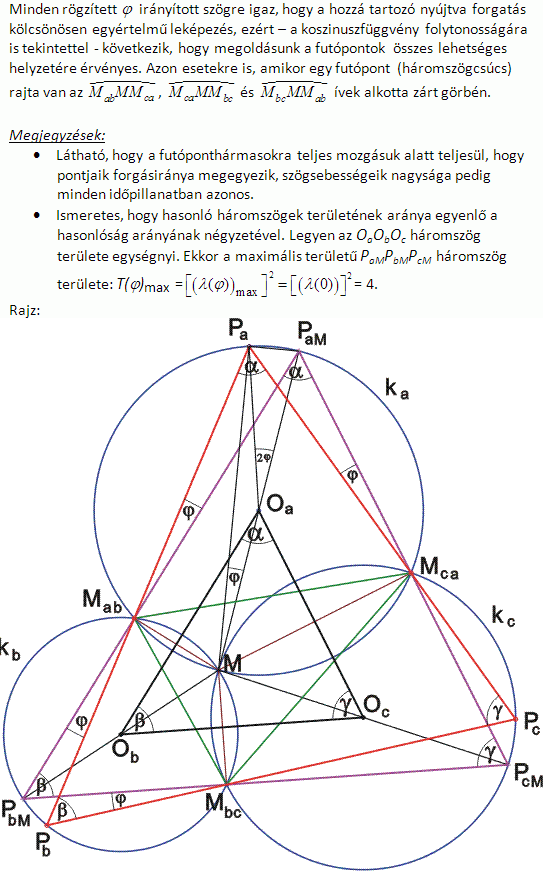
A három, egymást egy közös pontban metsző kör ábráját nézve feltünt, hogy az ábra szimmetrikus abban az értelemben, hogy egyik körnek sincs kitüntetett szerepe bármelyik másikkal szemben. Logikusnak véltem, hogy a megoldás is szimmetrikus: Ha a három körön futó pont valamelyike M-be kerül, akkor a másik kettő is. Ekkor persze vándorló háromszögünk elfajuló, egy pontra zsugorodik, alakjáról semmit sem mondhatunk – lásd NAGY BUMM hasonlatodat. De ha a futópontok közös M-beli helyzete megfelelő, akkor a feladat szabálya szerint a futópontok 180o-os elforgatottja, vagyis a - később indokolt módon - PaM,PbM,PcM -mel jelölt háromszög is megfelelő. Megrajzoltam PaM,PbM,PcM-et és úgy láttam, hogy oldalegyenesei áthaladnak az Mxy pontokon. Bebizonyítottam, hogy erre a háromszögre ez valóban igaz, és itt nekem is beugrott, valamelyik régi feladatban már szerepelt ez az ábra. Milyen jó lenne, ha a háromszögek többi helyzetében is az oldalegyenesek áthaladnának az Mxy pontokon! Beláttam, hogy tetszőleges ilyen Pa,Pb,Pc háromszög hasonló PaM,PbM,PcM-hez. Innen kezdtem el leírni a megoldást. A futópontok kezdeti felvétele tehát nem „Deus ex machina” módon, hanem az eddig leírtak alapján történt. Most már csak azt kellett igazolni, hogy az Mxy pontokra ileszkedő oldalegyenesekkel rendelkező háromszögek létrejönnek a futópontok kitűzésben leírt mozgása során.
|
| Előzmény: [1235] sakkmath, 2009-05-29 13:50:15 |
|
| [1235] sakkmath | 2009-05-29 13:50:15 |
 Örülök, hogy föltetted ezt a szép, a lényegre koncentráló megoldást! Köszönet érte. A feladatnak vannak egyéb, részben általad is jelzett, kidolgozásra érdemes részei, ezért most a magam részéről nem teszek ezeket érintő kiegészítéseket. Abban bízom, hogy valaki(k)nek lehetnek még saját eredményei(k) és 1-2 héten belül esetleg közli(k) azokat. Reagálnék viszont a kitűzési szöveggel kapcsolatos néhány megjegyzésedre, az estleges félreértések elkerülése végett. (Elnézést a terjedelemért.)
Mégegyszer: köszönöm és grat.
|
 |
| Előzmény: [1232] HoA, 2009-05-27 13:38:52 |
|
| [1234] m2mm | 2009-05-28 21:32:38 |
 Mivel a kör(ök) érinti(k) a tengelyeket, és (9,-2) pont x koordinátája pozitív, y koordinátája negatív, ezért a kör középpontjának x és y koordinátája ellentettei egymásnak, x pozitív, y negatív. A kör sugarának a hossza a középpont x koordinátájának nagysága, hiszen a kör érinti x-szet. A kör áthalad (9,-2) ponton, tehát: (9-r)2+(-2+r)2=r2, ahonnan r2-22r+85=0, amiből r értékére 5 illetve 17 adódik. Tehát a két kör egyenlete: (x-5)2+(y+5)2=25 illetve (x-17)2+(y+17)2=289.
|
| Előzmény: [1233] Luc, 2009-05-28 21:00:02 |
|
| [1233] Luc | 2009-05-28 21:00:02 |
 Sziasztok! Problémám akadt egy koordináta geometria feladattal: Meg kell adni annak a körnek(vagy köröknek) az egyenletét, amelyek áthaladnak (9;-2) ponton és érintik az x és y tengelyt is. Tudnátok segíteni, hogy hogy kell ezt kiszámolni?
|
|
| [1232] HoA | 2009-05-27 13:38:52 |
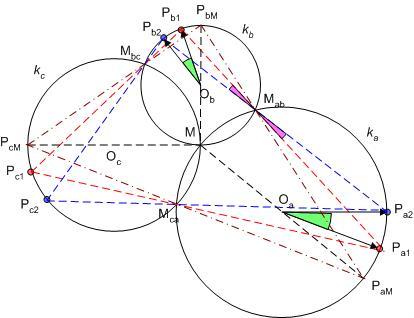
 1) Legyen a ka,kb,kc körök közös metszéspontja M, páronkénti második metszéspontjuk Mab,Mbc,Mca. Vegyük fel ka M-et nem tartalmazó MabMca ívén a Pa pontot. Legyen a PaMab egyenes és kb másik metszéspontja Pb , PbMbc egyenes és kc másik metszéspontja Pc . Könnyen belátható, hogy PcMca és McaPa párhuzamosak, vagyis egy egyenesen vannak. Különböző Pai -kat választva a keletkező PaiPbiPci háromszögek hasonlóak, hiszen például a Pai -knál fekvő szögek egyenlőek ka kör MabMca ívéhez tartozó kerületi szögével. Csak azt kell belátni, hogy ezen háromszögek csúcsai előállnak a feladatkitűzésben szereplő azonos, állandó szögsebességgel haladó futópontok egyidejű helyzeteként. Vegyünk fel két, 1-es és 2-es indexszel jelölt háromszöget. Pa1MabPa2 és Pb1MabPb2 szögek egyenlőek (csúcsszögek), a két körben a megfelelő ívhez tartozó kerületi szögek. Így a Pa1Pa2 és Pb1Pb2 ívekhez tartozó középponti szögek is egyenlőek, vagyis Pa és Pb ugyanakkora szögelfordulással jutnak ka-ban és kb-ben az 1-es helyzetből a 2-esbe, háromszögeink előállnak a feladatban megadott módon.
2) Nemcsak vándorló PaPbPc háromszögünk egyes helyzetei, hanem a részüket képező PaMPc háromszögek is hasonlók, hiszen egy-egy szögük az MMca húrhoz tartozó kerületi szög ka-ban ill. kc-ben. PaPbPc háromszög akkor lesz a legnagyobb területű, ha PaPc oldala a leghosszabb, vagyis ha PaMPc háromszög a legnagyobb. Ez pedig akkor következik be, amikor az M csúcshoz tartozó magasság a legnagyobb. Az utóbbi nem lehet nagyobb MMca -nál, és egyenlő is csak akkor, ha MMca merőleges PaPc-re. Legyen a csúcsoknak ez a helyzete PaM,PbM,PcM . A merőlegességből következik, hogy MPaM és MPcM átmérők – és ez belátható MPbM -re is.
Két megjegyzés:
a) Lássuk be, hogy háromszögünk akkor is megtartja alakját, mikor a ka-n futó pont az M-et tartalmazó MabMca íven halad.
b) PaM,PbM,PcM összetartozó ponthármas helyzetéből következik, hogy mindhárom körben 180o-ot fordulva mindhárom futópont M-be jut. Tehát , mint arra [1231]-ben utaltam, a körök metszéspontjában felvett futópont nem tilos, sőt a közös metszéspontban felvett 3 futópont éppen a megoldást adja.
152/3 feladatnak kitűzhetjük annak bizonyítását, hogy más megoldás nincs.
|
 |
| Előzmény: [1230] sakkmath, 2009-05-20 14:37:23 |
|
|
| [1230] sakkmath | 2009-05-20 14:37:23 |
 Az alábbiakban közlöm egy saját feladatomat. Nemrég rájöttem, hogy sajnos elődös: egy régi, közismert versenyfeladat következményének - vagy átfogalmazásának - is tekinthető.
152. feladat:
Egy adott ponton áthalad három, egymást páronként metsző kör. Mindegyik körön felveszünk egy-egy – a körök metszéspontjaitól különböző – pontot, melyek azonos körüljárási irányban befutják a körüket úgy, hogy egyszerre indulnak és azonos, állandó szögsebességgel haladnak.
1) Bizonyítsuk be, hogy e három pont felvehető úgy, hogy az általuk meghatározott háromszögek a teljes mozgás alatt hasonlóak legyenek egymáshoz.
2) Az így kapott háromszögek közül melyiknek a legnagyobb a területe?
|
|
| [1229] Editkesss | 2009-05-17 15:10:56 |
 De igen. A geometria nem az erősségem. (Ezeket a feladatokat már megoldottam . Abban viszont nem vagyok biztos, hogy jó is.) Ezért kértem segítséget!
|
|
|
| [1227] Editkesss | 2009-05-17 09:10:21 |
 Köszönöm szépen a segítséget! :) De lenne még egy-két feladatom! Az első: Tetszőleges e egyenes esetén jelölje: "Te" az e-re való tükrözést. Mutassuk meg, hogy ha "a" és "b" párhuzamos egyenesek, továbbá TaTbTcTaTbTc= identitás, akkor "c" is párhuzamos a-val és b-vel.
Második: Mutassuk meg, hogy ha az A1A2A3A4 és B1B2B3B4 négyszögek paralelogrammák, az AiBi szakasz Ai-hez legközelebbi negyedelőpontja Ni (i=1,2,3,4), akkor az N1N2N3N4 négyszög is (esetleg elfajuló) paralelogramma.
Előre is köszönöm!:)
|
|
| [1226] Euler | 2009-05-16 22:21:09 |
 A feladatot megpróbálom általánositva megoldani, vegyünk két nem egybeeső pontot, ekkor keressük azt a pontot a sikon, amelytől vett távolságaik négyzetösszege minimális, könnyen ellenőrizhető, hogy pont a két pontot összekötő szakasz felezőpontja lesz, pl. koordinátageometriával könnyen kijön,legyen A(a1;a2), B(b1;b2), a keresett pont: P(x;y), innen már csak egy másodfokú kifejezésnek kell vizsgálni a szélsőértkét, adódik az eredmény.Ez máshogy is kijöhet, bár itt nem biztos, hpogy "érdemes" igy gondolkodni, de ha mégis igy tesszük, akkor könnyen általánositható a probléma. Tudjuk ugyanis azt, hogy bármely háromszögben a szokásos jelölésekkel: 4sc2=2a2+2b2-c2(ez elég ismert összefüggésnek tekinthető,remélem.),a PAB háromszögre ezt felirva, kapjuk, hogy akkor lesz minimális a négyzetösszeg, ha a felezőponttól vett távolság minimális, máris adódik az eredmény. Kicsit továbblépve, vegyünk egy háromszöget(az egyszerűség kedvéért nem elfajulót), legyenek a csúcsai:A(a1;a2), B(b1;b2), C(c1;c2). keressük azt a pontot a sik egy adott egyenesén , amelytől vett távolságnégyzetösszeg minimális. Itt is hasonlóan eljárva, ráhúzodik a súlypontra az, ami előbb a felezőpontra húzodott rá,emiatt pedig az egyenesen lévő merőleges vetülete lesz a megfelelő pont.(Remélem érthető).Eljutottunk a Te problémádhoz, innen már "könnyű" elbánni vele, hiszen tekintsük az EBA és ECD háromszögeket, adódik, hogy akkor lesz mionimális a négyzetösszeg, ha az E-nek a CD és AB oldalak feletzőpontjától vett négyzetösszeg minimális, ez pedig használva az előzőeket, pontosan akkor lesz, ha a két felezőpont felezőpontjától vett távolság minimális, ez a pont pedig éppen a tetraéder súlypontja, ezt pl. vektorokkal lehet igazolni nagyon könnyen, igy itt a súlypontot kell merőlegesen vetiteni a sikra, ez lesz a keresett pont. Nyilván ha emeljük a dimenziószámot, hasonlóan adódik a feladat megoldása, csak maximum nem tudjuk elképzelni, hogy miről is szól a feladat. :-) remélem, tudtam segiteni a probléma megértésében.
|
| Előzmény: [1225] Editkesss, 2009-05-16 18:57:42 |
|
| [1225] Editkesss | 2009-05-16 18:57:42 |
 Hello, nekem egy olyan feladatom lenne, hogy adva van egy S sík és egy abcd tetraéder. veszünk egy E pontot . kérdés: Az S sík mely E pontjára lesz ez AE*2+BE*2+CE*2+DE*2 a kifejezés értéke a legkisebb? *2 a négyzetet jelöli!
|
|
|
| [1223] Vonka Vilmos Úr | 2009-05-15 15:46:44 |
 Akkor tényleg csak néhány ötlet:
1. és 2. Az adott ponton keresztül, amelynek a képét keressük, tekintsünk egy tetszőleges segédegyenest, és próbáld először ennek a képét megszerkeszteni.
3. A megfelelő egyenespár segítségével először határozzuk meg a kollineáció tengelyét, majd használjuk ki azt a tényt, hogy a centrum és az eltűnési egyenes távolsága megegyezik a tengely és az ideális egyenes képének távolságával.
4. A megfelelő egyenespár és egy pont ismeretében ismét először keressük meg a tengelyt. Majd válasszunk egy tetszőleges segédpontot azon az egyenesen, amelyiknek adott a képe; és próbáld a választott pont képét megszerkeszteni.
5. Az ABCD négyszög képe akkor lesz paralelogramma, ha a szemköztes oldalegyenesek metszéspontjaihoz a kollineáció ideális pontot rendel. Ez alapján határozd meg először az eltűnési egyenest. A tengely meghatározásához pedig tekintsünk ismét egy segédegyenest azon a ponton keresztül, amelynek a képe adott, és szerkesszük meg először a segédegyenes képét.
Remélem, innentől már menni fog!
|
| Előzmény: [1218] kandi, 2009-05-13 07:55:44 |
|
| [1222] kandi | 2009-05-15 10:42:38 |
 Köszönöm a linket, bár nem igazán értem az anyagot:( Amúgy centrális kollineációval oldhatók meg elvileg a feladatok és mi a projektív geometriával foglalkozunk. Ha mégis lenne még egy kis segítség mert én már kifuladtam a sz ötletekből?!
|
|
| [1221] jonas | 2009-05-14 21:55:55 |
 Én inkább ábrázoló geometriára tippelnék, bár szerencsére nekem nem kellett ilyesmit tanulnom, úgyhogy nem vagyok biztos, hogy valóban erről van szó.
|
| Előzmény: [1219] HoA, 2009-05-14 15:22:08 |
|
| [1220] HoA | 2009-05-14 16:14:44 |
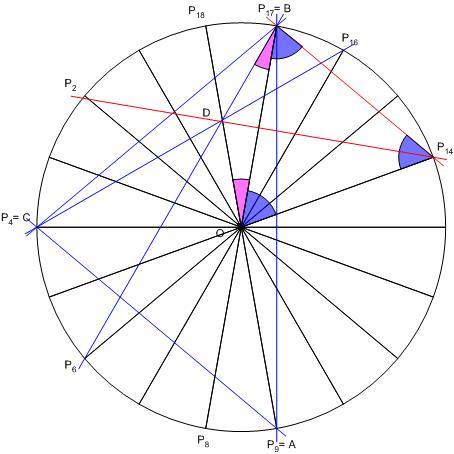
 Gratulálok! Igen, erre a megoldástípusra gondoltam! A D ponthoz tartozó bizonyításra egy másik változat: A definíció szerint D a P9P18 és P6P17 átlók metszéspontja, és azt kell igazolni, hogy P4P16-on is rajta van. DBO =20o ,mint a P6P8 ívhez tartozó kerületi szög. BOD =20o ,mint a P6P8 ívhez tartozó kerületi szög. BOD =20o ,mint a P17P18 ívhez tartozó középponti szög, OBD =20o ,mint a P17P18 ívhez tartozó középponti szög, OBD egyenlőszárú. P14OP17 egyenlőszárú. P14OP17 =60o ( 3 ívegység középponti szöge ) , P14OP17 =60o ( 3 ívegység középponti szöge ) , P14OP17 szabályos. Így BDOP14 deltoid, P17P14D szabályos. Így BDOP14 deltoid, P17P14D =30o . Így D rajta van a P14P17-tel 30o-ot bezáró P2P14 átlón és ennek P9P18 -ra vett tükörképén, P4P16-on is. =30o . Így D rajta van a P14P17-tel 30o-ot bezáró P2P14 átlón és ennek P9P18 -ra vett tükörképén, P4P16-on is.
|
 |
| Előzmény: [1216] sakkmath, 2009-05-12 15:24:47 |
|



 =EDA
=EDA /2 . Hasonlóan G’ az AC ív felezőpontja, G’DA’
/2 . Hasonlóan G’ az AC ív felezőpontja, G’DA’ /2. Ossza a DA egyenes ABC
/2. Ossza a DA egyenes ABC
 szögét BAD=
szögét BAD=


 a K,L,M pontokon átmenő kör. Bizonyítsuk be, hogy ha
a K,L,M pontokon átmenő kör. Bizonyítsuk be, hogy ha