Fórum: GEOMETRIA

Addig is egy projektív, de rövid megoldás 158/2re: B₁P₅R₂ és C₁P₂R₁ háromszögek megfelelő oldalegyenesei az egy egyenesbe eső A₁,A,M pontokban metszik egymást. A Desargues-tétel értelmében ekkor egy pontra nézve is perspektívek. Mivel C₁B₁ és P₂P₅ metszéspontja S, R₁R₂ is itt halad át.

Egy újabb, korrekt megoldást láttunk HoA-tól.

Azt hiszem, ideje megnevezni a jelenlegi feladatcsokor ősét, a KöMaL 1991. májusi számában megjelent F. 2857. feladatot. Ebből úgy kaptam például a B. 3869 - et, hogy a feladat szövegében az oldalfelező merőlegest egyszerűen kicseréltem szögfelezőre és különböző összefüggéseket vizsgáltam. Első eredményem az e hozzászólás végén (is) szereplő 158/3.' példa volt, amelyet félretéve jutottam el a végül közölt B. 3869 - hez.

Aki elmélyed a nevezett feladatokban, rájöhet, hogy némelyikben fontos szerep jut egy bizonyos hatszög főátlóinak. Érdemes tehát a feladatok általánosítását ezekre koncentrálva megkeresni. Annál is inkább, mert az a sejtésem, hogy HoA "P₁MP₄ kollinearitására van egy projektív megoldásom" bejelentése pont erre az általánosításra utalhat. Nézzük tehát feladataink eme "burkológörbéjét", melynek projektív megoldása Jolly Joker-ként gyorsan és sok mindent megválaszol (...):

TÉTEL: Adott az ABC háromszög és a belsejében egy M pont. Az AM, BM, CM egyeneseknek a körülírt körrel alkotott második metszéspontjai létrehozzák az A₁B₁C₁ háromszöget, melynek oldalai az ABC háromszög oldalait egy konvex hatszög csúcsaiban metszik. E hatszög főátlói az M pontban metszik egymást.

A 158/4/b. feladat szerkesztésének ígért kiterjesztését később, egy már beérkezett megoldás után célszerű feltennem.

Végül egy másik megoldás a 158/3. feladatra:

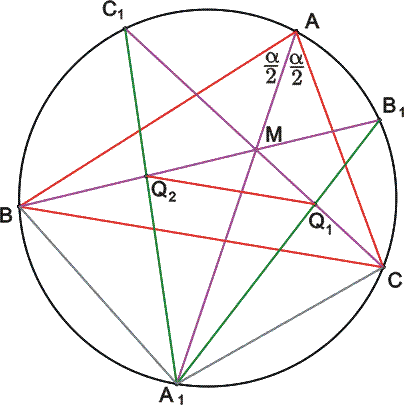
A 158/3. feladathoz: [1283] ábrájára is hivatkozva. Legyen ABC b és c oldalainak aránya k. AA₁ és BC metszéspontját jelöljük T-vel. szögfelezője az a oldalt ilyen arányban osztja, tehát CT=k^.BT . ABC és AP₂P₅ háromszögek hasonlóságából P₅M=k^.P₂M A₁P₂P₅ és A₁P₃P₄ háromszögek hasonlóságából P₄T=k^.P₃T , így CP₄=CT–P₄T=k(BT–P₃T)=k^.BP₃ . Q₁P₅M és Q₁P₄C illetve Q₂P₂M és Q₂P₃B hasonló háromszög párokban a hasonlóság aránya megegyezik, Q₁ ugyanolyan arányban osztja P₄P₅ -öt mint Q₂ P₃P₂ -t, a párhuzamos szelők tételének megfordításából Q₁Q₂ párhuzamos BC -vel.

P₁MP₄ kollinearitására van egy projektív megoldásom, de talán tud valaki erre is elemit?

158/4b.-re van egy Pascal tételes bizonyításom, ha mást nem érdekel a feladat, felteszem.

Köszönöm az elegáns megoldást!

Kérdésed után érdemes kitérni olyan további, ki nem mondott, de a [1283]-as ábráról könnyen leolvasható összefüggésekre (sejtésekre) is, melyeket szintén be lehet bizonyítani a projektív geometria alkalmazása nélkül. Egy ilyen a - dinamikus geometriai programok által sugalmazott - következő, 1. sejtés:

A P₁P₄ és P₃P₆ szakaszok (hatszögátlók) az M pontban metszik egymást. (Ha ennek igazolását feladatként tűzzük ki, ez a 158./5. feladat lehetne.)

Pár napon belül egy további sejtést is ismertetek, ami a 158/4/b. feladat szerkesztésének kiterjesztése lenne (örülnék, ha ebben valaki megelőzne a vonatkozó megoldásával).

Végül álljon itt egy "minimálábra" a 158./3. feladat megoldásához arra az esere, ha valakit zavarna a [1283]-as rajz zsúfoltsága:

... a projektív geometria mellőzésével.

A 158/3. feladat elemi geometriai módon megoldható.

A 158/1 feladathoz:

Legyen az AP₂P₅ körülírt köre k₁. BC és P₂P₅ párhuzamossága miatt AP₂P₅ és ABC hasonlóak, egymásból A középpontú nagyítással származtathatók, ez körülírt köreikre is áll, ezért k és k₁ A-ban érinti egymást, t a két kör hatványvonala. Ossza a CC₁ egyenes ABC szögét ₁=ACC₁ és ₂=C₁CB szögekre. Ekkor C₁B₁P₅=/2+₂ P₂BC₁=₁ BC₁P₂=/2 AP₂C₁=/2+₁ , P₅P₂C₁=/2+₁+ C₁B₁P₅+P₅P₂C₁=180^o , B₁C₁P₂P₅ húrnégyszög, körülírt köre legyen k₂ . B₁C₁ k és k₂ hatványvonala, P₂P₅ k₁ és k₂ hatványvonala. A három kör páronként vett hatványvonalai egy pontban metszik egymást (S)

A további feladatokra van valakinek nem projektív geometriai megoldása?

Nem erről van szó.

Olvassuk össze a következő sor vastagított részét: "C1-ből és L*-ból is béta szögben látszik az AM szakasz".

Tehát: a béta nagyságú látószög hiányzó szárát pótoltam.

Jogos! Kösz!

(Az AC1 berajzolása kicsit fölösleges azért! A C'-ből csak egy A jelű pontnak látszik.)

HoA [1278]-as megjegyzése a joke-ról találó ... :)

HoA [1276]-os kiegészítését elfogadva, az alábbi négy, piros puzzledarabkát helyezem el Bohner Géza [1274]-es megoldásában. Az így korrigált puzzle-t - Géza utólagos engedelmére számítva - idemásolom:

4/b. feladat: Szerkesszük meg a két ellipszis érintkezési pontjaihoz tartozó érintőit!

(Ez a részfeladat - a szerkesztési eljárást bemutató - bizonyítandó állítás formájában is megfogalmazható. Ez viszont könnyítést jelenthetne, s esetleg elrontanám vele a megoldó(k) örömét ...)

Egy saját feladatcsokrot

ajánlok a Fórum olvasóinak,

megoldóinak figyelmébe.

158. /1. - 4. feladatok:

Ezek után elárulhatom, hogy [1270] is egy, a [1274]-hez hasonló elemi geometriai megoldás átalakítása inverzióssá: AMNB₁ húrnégyszög, mert MN A-ból és B₁-ből is /2 szög alatt látszik. Így ANM=AB₁M=AB₁B=ACB. NM és BC párhuzamosak és a vége mint [1270] végén.

A "négy pont egy körön van" egyenértékű azzal, hogy egyiküket az inverzió középpontjának választva a másik három pont képe egy egyenesen van.

A puzzle 4 darabja még hiányzik, az egyikük rajzos. Ha holnap sem lesz, aki kirakja őket, vasárnap ezt megteszem én. (Ezek jelentősége már kisebb.)

A (1276)-os "foltozás" nem inverziós, de az eredeti első bekezdés meghagyásával létezik inverziós befejezés is. Igaz, ez keverék megoldást ad és elromlik a szimmetria.

Mint írtam:

"Az adott inverzióval játszva sok érdekességet láthatunk, kár, hogy a megoldásnál fölösleges!"

Azaz kár, hogy a megoldásnál fölösleges az inverzió!

Köszönöm PuzzleSmile-nak, hogy ismát ráirányította figyelmemet erre a megoldásra. Azt ugyan még nem árulta el, hogy hol a puzzle, de rájöttem, hogy ha már angolkodunk, akkor ez inkább joke. Ugyanis nem inverziós megoldás. Az első bekezdés helyett nyugodtan írhattuk volna: "Húzzunk párhuzamost M-en át BC-vel, az AB-vel alkotott metszéspont legyen L*. " Ettől persze még a bizonyítás helyes.

Bohner Gézának és Hoa-nak is köszönöm az érdekes, értékes megoldásokat.

Ha az ábrát kell szerinted kiegészíteni, áruld el, mire gondolsz. Ha a megoldás szövegét nem találod teljesnek, olvasd el a téma utolsó néhány heti hozzászólásait, melyek alapján az inverzió jópár tulajdonságát már ismertnek vesszük. Azt meg, hogy ML és BC párhuzamosságából következik LN és BC párhuzamossága, úgy értjük, mint [1270] végén: A C₁re leírtakat B₁re vonatkoztatva kapjuk, hogy MN és BC párhuzamos, tehát L,M,N egy egyenesen vannak és ez párhuzamos BC-vel.

Hoppá!! ... Ez egy puzzle!

157.feladat: egészítsük ki (1274)-et a hiányzó darabokkal!

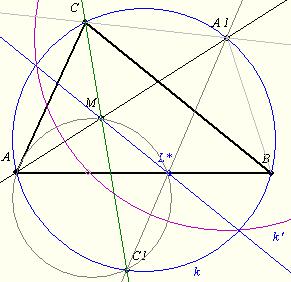
Legyen az inverzió az az A1 középpontú kör, melyre az A képe M. Ekkor a „k” körülírt kör képe az M-en átmenő BC-vel párhuzamos k’ egyenes. (A1 felezi a BC ívet.) Jelölje L* az AB és k’ metszéspontját.

Mivel C1-ből és L*-ból is béta szögben látszik az AM szakasz, az A, a C1, a L* és az M egy körön van. Ebben a körben a L*M és k-ban az A1C ív is alfa/2 szögben látszik, ezért C1, L* és A1 egy egyenesen van, azaz L* azonos L-lel. Ebből következik, hogy LN átmegy M-en és párhuzamos.

(Az adott inverzióval játszva sok érdekességet láthatunk, kár, hogy a megoldásnál fölösleges!)

A 9. sor vége helyesen: " és k₁ merőlegesen metszik"

A 2. rész:

Köszönöm Hoa szép megoldását. Úgy látszik, nincs több hozzászóló, ezért - két részletben - fölteszem saját inverziós levezetésemet, amely különbözik [1270]-től. Az 1. rész:

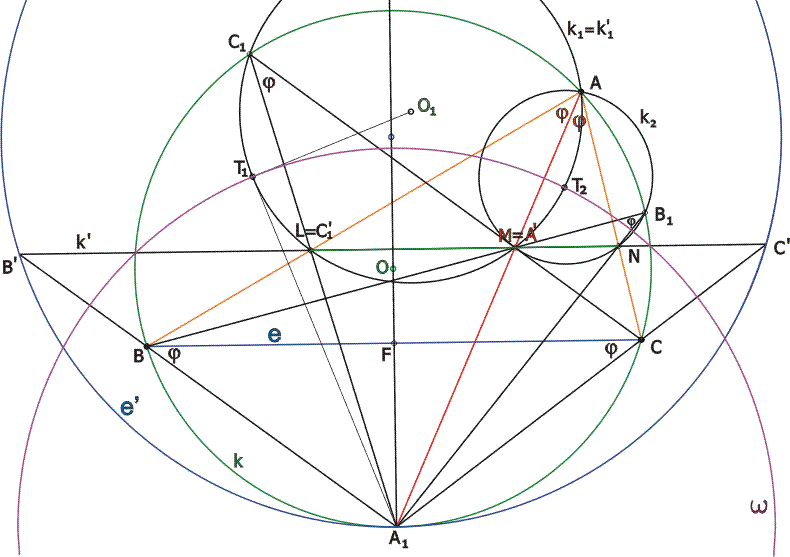
Az ABC háromszög körülírt köre k, középpontja O, a háromszög A csúcsában lévő szög 2. Az AA₁ szögfelező felezi a 2 szöget, ezért A₁AB = CAA₁ = , másrészt a BA₁ húron nyugvó kerületi szögek egyenlőségéből A₁AB = A₁B₁B =A₁CB= . Az A₁C húron nyugvó kerületi szögekre: CAA₁ = CC₁A₁ = CBA₁ = . Látható, hogy az LM szakasz a C₁ és az A pontból egyaránt szög alatt látszik. Ezért az L, M, A, és C₁ pontok egy k₁ körön sorakoznak, melynek középpontja O₁.

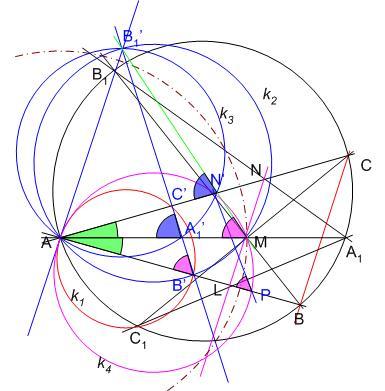
Legyen az inverzió alapköre az A középpontú, AM sugarú kör. Az inverz pontokat jelöljük vesszőzve. A körülírt kör képe egyenes, ezen jelöljük meg B’,C’,A₁’ésB₁’ pontokat. BC egyenes képe az AB’C’ pontokon át húzott k₁ kör, BB₁ képe az AB’MB₁’ pontok k₂ köre, A₁B₁ képe, k₃ , AA₁’N’B₁’ pontokon halad át, végül legyen k₄ kör az MN egyenes képe az AMN’ pontokon át. BAA₁=A₁AC=/2 . B₁’A₁’A=B₁’N’A (k₃ –ban közös húr ) . B₁’B’A=B₁’MA (k₂ –ben közös húr ) . Ezért B₁’M egyenes az AC és AA₁ egyenesekkel AB’A₁’ höz hasonló háromszöget alkot, ennek külső szöge megegyezik B₁’N’A-gel, B₁’,N’ésM egy egyenesen van. Legyen AB és k₄ másik metszéspontja P. N’PA=N’MA=C’B’A. AB’C’ és APN’ hasonló háromszögek, egymásból A középpontú nyújtással keletkeznek. Ez igaz körülírt köreikre is. A tehát k₁ és k₄ hasonlósági pontja, a két kör érinti egymást. Szimmetrikus módon a C₁’ -n áthaladó inverz körök vizsgálatával kapjuk, hogy az ML egyenes képe is a k₁ kör A középpontú nyújtásával keletkező, M-en áthaladó kör, vagyis k₄ ( és P = L’ ) . L,M, N egyazon egyenes pontjai, és mivel k₁ -nek és k₄ nek nincs A-tól különböző közös pontja, inverz képeik, a BC és LN egyenes párhuzamosak.