|
|
|
| [1318] HoA | 2009-11-26 12:07:57 |
 Illetve mégegyszer átolvasva, az "O-t tartalmazó" nyilván úgy értendő, hogy nem a körvonal, hanem a körlap tartalmazza O-t. Elnézést, Géza!
|
| Előzmény: [1317] HoA, 2009-11-26 12:05:38 |
|
|
| [1316] SmallPotato | 2009-11-25 17:54:58 |
 A szövegezés alapján nekem úgy tűnik, hogy k1 és k* egyaránt a k kört belülről érintő és k-hoz képest feleakkora sugarú kör. De akkor egyik metszéspontjuk O, miáltal a "jelölje ... k* és k1 metszéspontjait A és B" számomra nem igazán jól értelmezhető.
Rosszul értettem valamit?
|
| Előzmény: [1315] BohnerGéza, 2009-11-24 21:26:53 |
|
| [1315] BohnerGéza | 2009-11-24 21:26:53 |
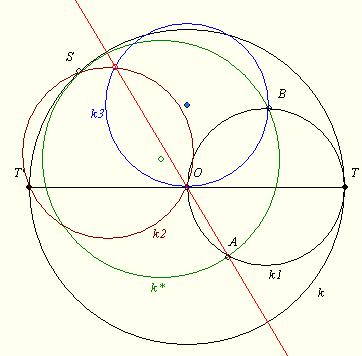
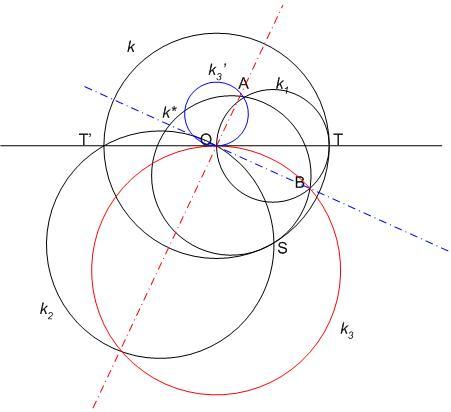
 Jelöljük k-val az O középpontú, az S és T ponton átmenő kört, T’-vel a T-ből induló átmérő másik végét. Legyen k1 az OT Thálesz-köre, k2 az S-en, T’-n és O-n átmenő kör. Jelölje k* a k-t belülről S-ben érintő, O-t tartalmazó kört és a k* és k1 metszéspontjait A és B. Már csak a k3-at határozom meg, jelölje a TT’-t O-ban érintő B-n átmenő kört. Bizonyítandó, hogy a k2 és k3 metszéspontjain átmenő egyenes tartalmazza A-t.
|
|
|
| [1313] sakkmath | 2009-11-23 11:17:38 |
 Megvizsgálhatók azok az esetek is, amikor M-et a DA1 szakasz D-n, illetve A1-en túli meghosszabbításain mozgatjuk. A Cabri kiírással jelzi, hogy az M által bejárt útvonal egyes csatlakozó szakaszain éppen milyen kúpszelet  1 és 1 és  2. (Van olyan szakasz is, amikor egy lokális kúpszeletről nem tudja megmondani, hogy az konkrétan melyik, s ez nyilván a program úgynevezett modellhibájával magyarázható.) Érdemes lenne kideríteni, hogy a kiinduló szerkesztéssel milyen kapcsolatban vannak ezek a fázisváltások, melyeknél tehát az egyik kúpszeletfajtából hirtelen egy másikba vált 2. (Van olyan szakasz is, amikor egy lokális kúpszeletről nem tudja megmondani, hogy az konkrétan melyik, s ez nyilván a program úgynevezett modellhibájával magyarázható.) Érdemes lenne kideríteni, hogy a kiinduló szerkesztéssel milyen kapcsolatban vannak ezek a fázisváltások, melyeknél tehát az egyik kúpszeletfajtából hirtelen egy másikba vált  1, vagy 1, vagy  2. Vajon megszerkeszthetők-e az ilyen váltásokhoz tartozó M-ek? 2. Vajon megszerkeszthetők-e az ilyen váltásokhoz tartozó M-ek?
Mindezt nem feladatkitűzésként, hanem egyfajta töprengő lezárásként írtam. Úgy tűnik ugyanis, hogy ez az új kérdéskör – legyen bármennyire ígéretes és izgalmas – túlmutat e FÓRUM jellegén és keretein, és persze az én igencsak szerény ismereteimen :(.
Ismét megköszönöm HoA hozzászólásait, megoldásait. Sokat tanultam belőlük.
|
| Előzmény: [1312] HoA, 2009-11-11 14:59:44 |
|
|
|
| [1310] HoA | 2009-11-11 14:58:12 |
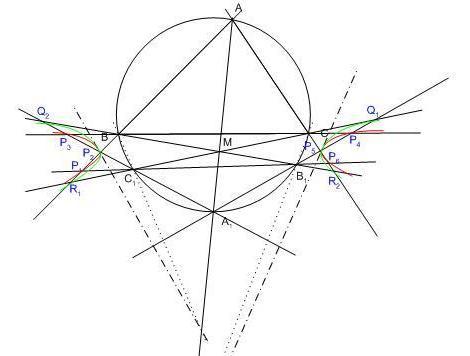
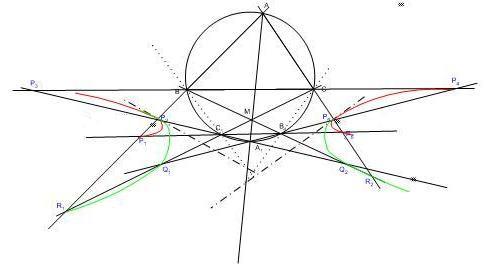
 M-et DA1-en mozgatva (D az ábrákról lemaradt) azt tapasztaljuk, hogy  1 és 1 és  2 hiperbola - a hat-hat pont nem konvex sokszöget alkot, a kúpszelet bizonyításnál pedig nem használtuk ki, hogy M a háromszögön belül van. Amíg M D-hez van közel, Q1 az AA1 egyenesnek C-vel, Q2 pedig a B-vel azonos oldalán van. (1.ábra) . Ha M A1-hez van közel, fordított a helyzet (2.ábra). A két esetet az az M0 választja el, amelyre CC1 és A1B1 párhuzamos. (3. ábra). Mivel A1B1B 2 hiperbola - a hat-hat pont nem konvex sokszöget alkot, a kúpszelet bizonyításnál pedig nem használtuk ki, hogy M a háromszögön belül van. Amíg M D-hez van közel, Q1 az AA1 egyenesnek C-vel, Q2 pedig a B-vel azonos oldalán van. (1.ábra) . Ha M A1-hez van közel, fordított a helyzet (2.ábra). A két esetet az az M0 választja el, amelyre CC1 és A1B1 párhuzamos. (3. ábra). Mivel A1B1B =A1AB =A1AB = = /2 , váltószöge B1MC /2 , váltószöge B1MC is ekkora, CMB is ekkora, CMB = = - - /2, M ekkor BC ilyen látószögű körívén van. Ha BC felezőmerőlegese k-t az A1-től különböző A2-ben metszi, M0 éppen az A2 középpontú, A2B sugarú kör és az AA1 egyenes metszéspontja. Ekkor BB1 és A1C1 is párhuzamos, Q1 és Q2 a végesben nem jön létre, hanem annak a hiperbolának a végtelen távoli pontjai, amelyik a P2P5R1R2 pontokon halad át és aszimptotái BB1 és CC1 irányúak. /2, M ekkor BC ilyen látószögű körívén van. Ha BC felezőmerőlegese k-t az A1-től különböző A2-ben metszi, M0 éppen az A2 középpontú, A2B sugarú kör és az AA1 egyenes metszéspontja. Ekkor BB1 és A1C1 is párhuzamos, Q1 és Q2 a végesben nem jön létre, hanem annak a hiperbolának a végtelen távoli pontjai, amelyik a P2P5R1R2 pontokon halad át és aszimptotái BB1 és CC1 irányúak.
Ez azonban nem a 158/6. feladat 2. pontjában keresett M0, hiszen a P2 illetve P5-beli érintőkre továbbra is igaz, hogy BC1 ill. CB1 és AA1 metszéspontján haladnak át, márpedig a szemlélet alapján R1 és R2 nincsenek ezen a két érintő egyenesen.
|
 |
| Előzmény: [1308] sakkmath, 2009-10-31 12:25:42 |
|
| [1309] HoA | 2009-10-31 17:10:08 |
 Eddig nem ismertem, de sajnos most sem igazán. Oda belépve ugyanis csak egy csomó hirdetés jelent meg - meg egy anchor a www.komal.hu- ra - valamint egy kiírás , hogy "Az Internet Explorer nem tudja megjeleníteni" , de hogy mit, az már nem látszik. Talán valami újabb böngészőt igényel.
|
| Előzmény: [1307] Zsodris, 2009-10-31 10:38:14 |
|
|
| [1307] Zsodris | 2009-10-31 10:38:14 |
 Sziasztok!
Ismeritek a www.silverpen.eu oldalt?
Szerintem a legjobb ingyenes vektorgrafikus program. Telepíteni sem kell. Ideális geometriai feladatok feladásához, megoldásához.
|
 |
|
|
| [1305] HoA | 2009-10-26 10:38:11 |
 Bár az eddigiekből következik, mivel tételesen még nem szerepelt 158/4/b megoldása, megadom: A hatszög csúcsait R1P2Q2R2P5Q1 sorrendben véve
R1P2 R2P5=A R2P5=A
P2Q2 P5Q1=A1 P5Q1=A1
Q2R2 Q1R1=M Q1R1=M
, a három metszéspont egy egyenesen van, így a hat csúcs egy kúpszeleten helyezkedik el. ( Hogy ez ellipszis-e, arra ld. [1299] )
Ezután rátérhetünk 158/4/c –re. P1P2P3P4P5P6 ellipszisének P2-beli érintője legyen t1, ennek P4P6-tal alkotott metszéspontja T . A P2P2P3P4P6P1 ellipszisbe írt „hatszögre”
P2P2(=t1) P4P6=T P4P6=T
P2P3 P6P1=C1 P6P1=C1
P3P4 P1P2=B P1P2=B
, T rajta van a BC1 egyenesen. A P2P2P5P4P6P3 hatszögre
P2P2(=t1) P4P6=T P4P6=T
P2P5 P6P3=M P6P3=M
P5P4 P3P2=A1 P3P2=A1
, T rajta van az MA1 egyenesen. T tehát BC1 és MA1 metszéspontja, t1 a P2T egyenes.
R1P2Q2Q1P5R2 ellipszisének P2-beli érintője legyen t2, ennek Q1R2-vel alkotott metszéspontja U . A P2P2R1Q1R2Q2 ellipszisbe írt hatszögre
P2P2(=t2) Q1R2=U Q1R2=U
P2R1 R2Q2=B R2Q2=B
R1Q1 Q2P2=C1 Q2P2=C1
, U rajta van a BC1 egyenesen. A P2P2P5Q1R2Q2 ellipszisbe írt hatszögre
P2P2(=t2) Q1R2=U Q1R2=U
P2P5 R2Q2=M R2Q2=M
P5Q1 Q2P2=A1 Q2P2=A1
, U rajta van az MA1 egyenesen. U tehát BC1 és MA1 metszéspontja, t2 a P2U egyenes. Vagyis T=U és így t1=t2, a két ellipszis P2 -beli érintője közös, érintik egymást. Az ábra szimmetriája miatt P5 -re hasonló bizonyítás adható.
|
| Előzmény: [1293] sakkmath, 2009-10-06 17:56:28 |
|
| [1304] sakkmath | 2009-10-26 09:50:51 |
 Egyetértek HoA értékelésével. Most már nekem is úgy tűnik, hogy B.3869-ben nem lehet elemi eszközökkel bebizonyítani a BC-vel nem párhuzamos hatszögfőátlók M-re illeszkedését. Az elmúlt napokban sokat kísérleteztem e témában, de eredménytelenül. Köszönet illeti HoA-t - s talán még valakit :) -, hogy a helyzet tisztázódott.
|
| Előzmény: [1301] HoA, 2009-10-20 16:17:28 |
|
| [1301] HoA | 2009-10-20 16:17:28 |
 Sajnos elképzelhetőnek tartom, hogy B.3869 és F.2857 olyan értelemben ikrek, hogy B.3869 –ben , ahol M a szögfelezőn van, valójában azt lehet bizonyítani elemi eszközökkel, hogy a hatszög BC-vel párhuzamos átlója átmegy M-en – és a másik két átlóról nem sikerül, míg F.2857-ben, ahol M az oldalfelező merőlegesen van, nem véletlenül azt kell – és lehet – elemi úton bizonyítani, hogy a hatszög átlói között van két olyan, amelyik M-ben metszi egymást – és az oldalfelezőre merőleges oldallal „párhuzamos” hatszögátlóról nem esik szó.
|
| Előzmény: [1300] sakkmath, 2009-10-14 17:45:24 |
|
| [1300] sakkmath | 2009-10-14 17:45:24 |
 Köszönöm HoA újabb megoldásait.
Ha jól értem, a 2)-es kérdés így fejthető ki: Ismerek-e olyan bizonyítást, ami úgy igazolja azt, hogy a Pi hatszög kúpszeletbe írt, hogy közben nem használja fel a főátlók azon tulajdonságát, hogy áthaladnak az M ponton?
A válaszom: nem ismerek ilyen bizonyítást és attól tartok, hogy talán nem is létezik ilyen. Lehetséges viszont, hogy e bizonyítás létezésének eldöntéséhez közelebb vinne, ha valaki elemi úton megoldaná 158/5 ama esetét, amikor M a szögfelezőn van. Ez utóbbi elemi bizonyítás biztosan létezik, hiszen az ikerfeladat F. 2857-re is van elemi bizonyítás (a KöMaL közölt egy ilyet anno)...
Elképzelhető, hogy a vizsgált feladatcsoport egy újabb kiterjesztése is közelebb visz a 2)-es a kérdésben megjelölt bizonyítás létezésének megítéléséhez. (Ezt a kiterjesztést később közölném, a továbbiakban beérkező megoldás(ok) után, ugyanis azokkal is összefügg.)
|
| Előzmény: [1299] HoA, 2009-10-14 11:07:37 |
|
| [1299] HoA | 2009-10-14 11:07:37 |
 Azt hiszem nem lövöm le a többi alfeladatra beérkező megoldásokat és nem okozok meglepetést, ha megadom 158/4/a megoldását : A hatszög csúcsait P1P2P5P4P3P6 sorrendben felvéve a „szemközti” oldalak metszéspontjai B,MésB1 , egy egyenesre esnek, így a hat pont egy ellipszisen – vagy legalábbis egy kúpszeleten helyezkedik el.
Kérdéseim: 1) A szemléleten kívül mi igazolja, hogy a kúpszelet ellipszis? – Természetesen nem a görbe egyenletének együtthatóiból képezhető determinánsok vizsgálatára gondolok. 2) Sakkmath tud-e 158/4/a-ra 158/5-öt nem felhasználó megoldást?
|
| Előzmény: [1293] sakkmath, 2009-10-06 17:56:28 |
|
| [1298] HoA | 2009-10-12 15:18:42 |
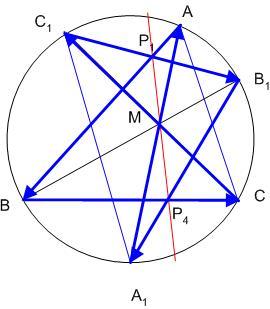
 [1293] TÉTEL-ének - és egyben 158/5nek a bizonyítása: A [1283]-éhoz hasonló ábra csak a könnyebb azonosíthatóság kedvéért. Nem használjuk ki, hogy körülírt körről van szó, tetszőleges kúpszelet lehet, és M-ről sem tesszük fel, hogy a szögfelezőn van. Az ABCA1B1C1 hatszög csúcsainak megfelelő sorrendezésével a Pascal-tétel szerint adódik a TÉTEL állítása. Más sorrendezéssel a másik két átlóról ugyanígy kimutatható, hogy M-en haladnak át.
|
 |
| Előzmény: [1296] sakkmath, 2009-10-09 11:46:36 |
|
|
| [1296] sakkmath | 2009-10-09 11:46:36 |
 Ez a megoldási kísérlet érdekes és visszautal a feladatok gyártástechnológiáját megvilágító egykori "oldalfelező merőleges - szögfelező" cserére.
Ha bebizonyítjuk [1293] TÉTELét (ami voltaképpen - kis bővítéssel - a már említett 158/5. feladat), az egyik lehetséges bizonyításból (Pascal ...) az is kiderülhet, hogy a sejtés erősíthető: az ellipszisen túl, más kúpszeletekre is igaz az állítás.
Most jutott eszembe egy másik, (esetleg) szóba jövő bizonyítási módszer, a Brianchon-os. De ez (ha egyáltalán jó irány) messzire vezet, időigényes, inkább nem részletezem ...
|
| Előzmény: [1295] HoA, 2009-10-07 15:55:37 |
|
| [1295] HoA | 2009-10-07 15:55:37 |
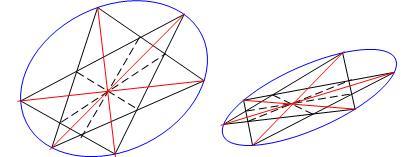
 158/4 megoldási kisérletei során merült fel az ötlet: vessük alá az ábrát egy olyan projektivitásnak, mely B-t és C-t helyben hagyja, A-t és M-et viszont BC felező merőlegesére viszi. Ekkor az egyenesek egyenesek maradnak, de a körülírt kör már nem lesz kör. Innen a sejtés: [1293] TÉTEL-e erősíthető: nem kell a körülírt kör, ellipszisre is igaz az állítás.
|
 |
| Előzmény: [1293] sakkmath, 2009-10-06 17:56:28 |
|






 1 és
1 és 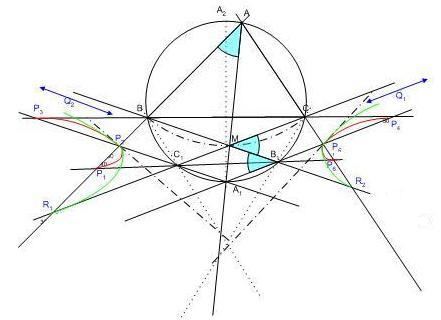
 =A1AB
=A1AB /2 , váltószöge B1MC
/2 , váltószöge B1MC -
-



 R2P5=A
R2P5=A
