| [1430] HoA | 2010-06-16 12:25:39 |
 A 165. [1422] feladat megoldása. E fórum olvasóinak, feladatmegoldóinak sokkal tömörebben is elég lenne, de szerintem tanításban jól használható, így kicsit részletesebben írok.
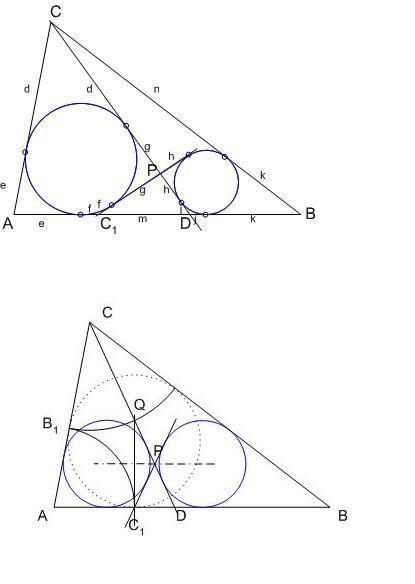
a) Legyen egyelőre ABC beírt körének érintési pontja AB-n C* . C* az az AB szakaszon lévő pont, melyre az A-tól és B-től mért távolságok különbsége ugyanakkora, mint C-re. Ennek igazolásához elég a csúcsokból a beírt körhöz húzható érintőszakaszok s-a és s-b kifejezéseire hivatkozni. Megmutatjuk, hogy ez C1-re is igaz, tehát C*=C1. Igazoljuk, hogy BC1–AC1=BC-AC , vagyis [BC1–AC1]–[BC-AC]=0 . Az ábrán a kisbetükkel jelölt egyenlő érintőszakaszokkal, valamint n=d+g+h és j+m=f+g+h felhasználásával [(k+j+m)–(e+f)]–[(k+n)-(d+e)]=[j+m-f]-[n-d]=[g+h]-[g+h]=0
b) Ennek alapján megállapíthatjuk, hogy van olyan A és B fókuszú hiperbola, mely C-n és C1-en is áthalad. A fenti képletet átrendezve [BC-BC1]–[AC–AC1]=0 , ami viszont azt jelenti, hogy van olyan C és C1 fókuszú hiperbola, mely A-n és B-n is áthalad. Erről kell belátni, hogy P-n is áthalad, vagyis [PC-PC1]–[AC–AC1]=0 . Az ábra érintőszakaszaival [(d+g)-(g+f)]–[(d+e)–(e+f)]=[d-f]–[d–f]=0 . A háromszögbe eső parabolaív minden P’ pontja kiadódik P-nek, ha D-t CP’ és AB metszéspontjának választjuk.
c) A két kör közös belső érintői szimmetrikusak a két kör centrálisára, a centrális felezi a CPC1 szöget, tehát érintője a hiperbolának. Egyenlő sugarak esetén a centrális párhuzamos AB-vel.
d) Visszavezettük a feladatot adott hiperbola adott irányú érintőjének és a P érintési pontnak a szerkesztésére. Tekintsük a hiperbolát mint az F1 középpontú vezérkört érintő és F2-n áthaladó körök középpontjának mértani helyét. F2-nek a P-beli érintőre vett F2’ tükörképe a vezérkör és a PF1 egyenes metszéspontja, F2F2’ merőleges az érintőre. A szerkesztés: Húzzunk F2-n át merőlegest egy érintőirányú egyenesre, ennek a vezérkörrel alkotott (egyik) metszéspontja F2’ , F2F2’ felező merőlegese az e érintő, e és F1F2’ metszéspontja a P érintési pont. Feladatunkban A a hiperbola pontja, az A körüli, C1-en áthaladó kör és az AC szakasz B1 metszéspontja rajta van a C körüli vezérkörön. Az ABre C1-ben emelt merőleges és a C körüli CB1 sugarú kör (egyik) metszéspontja legyen Q . A D pont CQ és AB metszéspontjaként adódik.
Ehhez a szerkesztéshez most már a hiperbola felhasználása nélkül is eljuthatunk. Ha a két kör sugara egyenlő, akkor közös belső érintőik tükrösek az AB -val párhuzamos centrálisra. Legyen Q a PC szakasznak az a pontja, melyre PQ=PC1. PQC1 egyenlőszárú háromszög C1Q alapja merőleges AB-re, Q rajta van az AB -re C1-ben emelt merőlegesen. Másrészt CQ=PC–PC1=AC–AC1 . Az AC szakaszra ráforgatva az AC1 távolságot a végpont legyen B1 . CB1=AC–AC1 . Q rajta van a C körüli CB1 sugarú körön, innen a szerkesztés a fenti.
|
 |
| Előzmény: [1422] BohnerGéza, 2010-06-03 16:31:30 |
|
|
| [1428] BohnerGéza | 2010-06-05 13:01:10 |
 Felhasználandó a 168. feladatban:
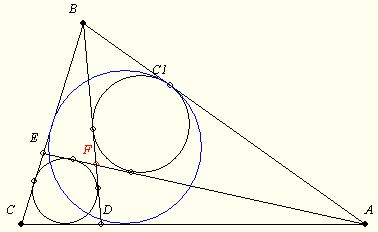
169. feladat: Az ABC háromszög AC illetve BC oldalán vegyük föl a D illetve E pontot úgy, hogy az AEC és BCD beírt köre azonos legyen: k1. Az AE és BD metszéspontja legyen F. Jelölje k2 az ABF beírt körét, érintse ez C1-ben AB-t. Igazoljuk, ha a CA-n mozgatjuk D-t (E és F megfelelően mozog), akkor C1 nem mozog. (Az ABC beírt körének pontja.)
|
 |
| Előzmény: [1427] BohnerGéza, 2010-06-05 12:53:18 |
|
| [1427] BohnerGéza | 2010-06-05 12:53:18 |
 Valóban! Pontosítva az [1406]-ban említett AD-feladatot:
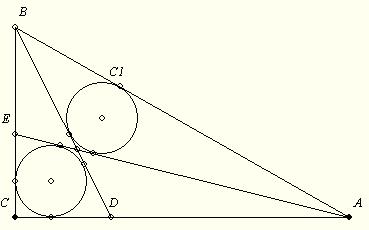
168. feladat: Az ABC C-nél derékszögű háromszög AC illetve BC oldalán vegyük föl a D illetve E pontot úgy, hogy az AEC és BCD beírt köre azonos legyen: k1. Az AE és BD metszéspontja legyen F. Jelölje k2 az ABF beírt körét.
Fejezzük ki az ABC oldalai segítségével k1 sugarát, ha egyenlő a k2-ével!
|
 |
| Előzmény: [1424] HoA, 2010-06-05 09:01:13 |
|
|
| [1425] BohnerGéza | 2010-06-05 11:26:21 |
 167. feladat: Tekintsük az AFG háromszög k körülírt és C középpontú beírt körét. Legyen B a k tetszőleges pontja, a B-ből a beírt körhöz húzott érintők messék k-t még D-ben illetve E-ben. Igazoljuk, hogy DE érinti a beírt kört, azaz AFG és BDE beírt köre azonos.
Az [1409]- ben lévő 165. feladat bizonyításához elég megmutatni: Ha B-t k és AC másik metszéspontjának vesszük, szimmetria miatt elég belátni, hogy B egyenlő távol van F-től és C-től.
|
| Előzmény: [1409] HoA, 2010-04-23 17:24:22 |
|
|
|
| [1422] BohnerGéza | 2010-06-03 16:31:30 |
 A B.4269 feladattal kapcsolatban keletkezett a hozzászólás. Érdemes a "Lejárt határidejű KÖMAL feladatokról" című téma 552. hozzászólását is megnézni.
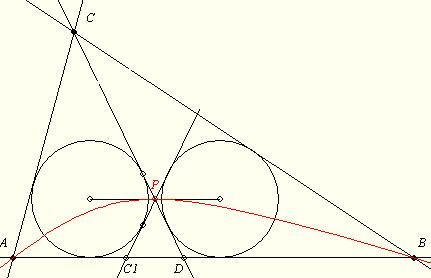
Az ABC háromszög AB oldalán mozgatjuk a D pontot. Az ADC és DBC beírt körének másik (nem CD) közös belső érintője AB-t a C1-ben metszi. A két belső érintő metszéspontja P. Mutassuk meg a következőket:
165. feladat: a.) Igazoljuk, hogy C1 nem függ D-től! (ABC beírt körének pontja)
b.) Igazoljuk, hogy a P pontok halmaza a C és C1 fókuszú és A-n átmenő hiperbola A-n (és B-n) átmenő ágának a háromszögbe eső része!
c.) Igazoljuk, hogy a két kör sugara akkor egyforma, ha a hiperbola P-ben húzott érintője párhuzamos AB-vel!
d.) A fentiek alapján szerkesztendő az a D, melyre a két kör sugara egyenlő!
|
 |
|
| [1421] kuklic | 2010-06-01 22:03:10 |
 Nagyon szépen köszönöm :) Elég jó vagy :D ezt magamtól nem biztos, hogy megláttam volna :)
|
|
| [1420] HoA | 2010-06-01 17:01:37 |
 A négy hasonló derékszögű háromszögből is szépen kijön, de talán a legegyszerűbb, ha észrevesszük, hogy az A1 -nél és B1 -nél lévő derékszögek miatt A1 és B1 rajta van AB Thálesz-körén, így ABA1B1 húrnégyszög, a szelőtétel éppen a kívánt egyenlőséget adja.
|
| Előzmény: [1419] kuklic, 2010-06-01 16:38:56 |
|
| [1419] kuklic | 2010-06-01 16:38:56 |
 Hello mindenki Egy kis segítséget kérnék. Ezzel a feladattal elakadtam:
Az ABC hegyesszögű háromszög A-ból induló magasságvonalának BC-vel való metszéspontja A1, B-ből induló magasságvonalának AC-vel való metszéspontja B1, magasságpontja M. Igazolja, hogy AM*MA1=BM*MB1!
|
|
| [1418] Hajba Károly | 2010-04-29 00:24:00 |
 Én egy kicsit másképpen oldottam meg, de HoA ábráját felhasználva már könnyebben megérthető.
A belső ötszög belső szögei: 5*180-360 = 540. Azaz az ötszögön belül kijelölsz egy pontot és 5 háromszöget képezel az öt pontból 2-2 szomszédos pont ill. a központi pont segítségével. Ez az öt háromszög teljesen kitölti a belső ötszöget. Az öt háromszög belső szögeinek összegéből levonod a központi ponthoz tartozó 360 fokot és így kapod az ötszög belső szögeinek összegét. Eddig talán nem is volt újdonság.
A külső szögeinek összegét úgy kapjuk, hogy az öt pont teljes szögeiből levonjuk a belső szögeket. 5*360-540 = 1260.
Most a belső ötszög külső oldalára 5 háromszöget illesztünk úgy, hogy épp a kívánt csillagötszöget adja ki. Itt a háromszögek belső 2-2 szögei részei az ötszög külső szögei tartományának. S közöttük épp a csúcsszög miatt épp a belső szög a különbség. Azaz, ha az ötszög külső szögeinek összegéből levonom a belső szögeinek összegét, akkor a háromszögek a belső ötszöggel érintkező 2-2 szög összegét kapjuk.
Vagyis ha az 5 háromszög szögösszegéből levonjuk a belső ötszög külső szögeit és hozzáadjuk a belső szögeit, akkor épp a csúcsszögek összegét kapjuk.
5*180 - 1260 + 540 = 180
Ha lesett a tantusz vagy kisült az isteni szikra, akkor már egyszerűbb, mint ahogy most leírtam.
|
| Előzmény: [1415] Cseri, 2010-04-27 23:46:12 |
|
|
| [1416] HoA | 2010-04-28 13:36:46 |
 Megoldásod annyiban vázlat, hogy abból, hogy a két háromszög beírt körének C a középpontja, még nem következik, hogy a hatszögbe kör írható, csak akkor, ha azt is igazoljuk, hogy a háromszögek beírt köreinek egyenlő a sugara - a beírt körök egybeesnek.
|
| Előzmény: [1414] lorantfy, 2010-04-27 21:33:10 |
|
| [1415] Cseri | 2010-04-27 23:46:12 |
 Üdvözlök mindenkit!
En egy uj vendeg vagyok ezen a weboldalon. Es lenne egy kerdesem. Esetleg valaki tudna nekem segiteni??!! Egy nem szabalyos csillagötszögröl ( pentagramma ) van szo. Be kell bizonyitani, hogy az öt csillagcsucsban levö szögeinek összege 180 fok. Ezt a szabalyos csillagötszögben be tudom bizonyitani,de a nem szabalyosban nem. Van esetleg valakinek ötlete?? Segitsegeteket elöre is köszönöm. Cseri Nemetorszagbol
|
|
| [1414] lorantfy | 2010-04-27 21:33:10 |
 Megoldásvázlat a 165.höz: A k körben AD és AE ívek valamint a BG és BF ívek egyenlők, mert a k1 illetve a k2 kör vágja ki őket. Így az AB húr az AFG és BDE háromszögben is szögfelező. FAC szög=GAC szög és AB a k2 körnek is szimmetria tengelye, így azonos íveket vág ki a k2 körből. Ez már bizonyítja, hogy GC is szöfelező, így C lesz az AFG háromszög beírt körének középpontja. Hasonlóan a másik, BDE háromszögre is, vagyis az említett hatszögnek is beírt köre. Ahogy lesz időm rajzolok egy ábrát. Jó példa! Köszönet érte!
|
| Előzmény: [1409] HoA, 2010-04-23 17:24:22 |
|
| [1413] Rozali | 2010-04-26 08:25:08 |
 Szia! Nagyon szépen köszönöm a segítséget !! Így már menni fog remélem!
|
|
| [1412] Tauthorne | 2010-04-25 16:18:50 |
 Bocsi, előző üzenetben véletlenül elírtam a legvégét: 7x+5y=-13 az egyenlete
|
|
| [1411] Tauthorne | 2010-04-25 16:14:57 |
 Szia! Mivel merőleges az adott egyenesre, ezért annak normálvektora (5,-7) az pont jó lesz a keresett egyenes irányvektorának. Az irányvektoros egyenlet pedig: v2x0-v1y0=v2x-v1y ,beirva a számokat: (-7)*(-4)-5*3=-7x-5y tehát:7x+5y=43
|
|
| [1410] Rozali | 2010-04-25 13:46:24 |
 Sziasztok! Megcsinálná ezt valaki nekem? Adjuk meg annak az egyenesnek az egyenletét, amely merőleges az 5x-7y=-17 egyenletű egyenesre,és átmegy a P(-4;3) ponton!
és ha kérhetem magyarázza is el mert lemaradtam és nem értem!!!!!!
Előre is nagyon köszi holnapra kellene!
|
|
| [1409] HoA | 2010-04-23 17:24:22 |
 Javaslat a 165. feladatra:
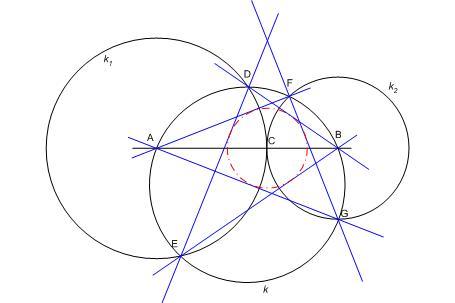
A k kör AB húrjának belső ponja C . Az A középpontú, C-n áthaladó k1 kör és k metszésponjai D és E, a B középpontú, C-n áthaladó k2 kör és k metszésponjai F és G . Bizonyítsuk be, hogy az AF , AG, BD , BE , DE és FG egyenesek által határolt hatszögbe C középpontú kör írható.
|
 |
|
|
| [1407] HoA | 2010-04-23 14:47:56 |
 1) Ha F a BC oldal belső pontja, akkor AF és BC metszéspontja F. Nem AF és BE metszéspontjáról van szó?
2) Ekkor viszont CFME nem lehet húrnégyszög, hiszen C-nél derékszögű, tehát M-nél is derékszögűnek kéne lennie, de a definíció szerint M a háromszög belső pontja és így az AB feletti Thálesz-körnek is belső ponja, vagyis FME szög = AMB szög > 90 fok. Mivel belé írható körről írsz, nem inkább érintőnégyszög?
|
| Előzmény: [1406] m2mm, 2010-04-23 14:29:17 |
|
| [1406] m2mm | 2010-04-23 14:29:17 |
 Tegnap volt kitűzve Arany Dánielen a következő(nem szó szerint ez volt a szöveg): Egy ABC C-ben derékszögű háromszög AC oldalának E, BC oldalának F belső pontja, AF és BC metszéspontja M. CFME húrnégyszög, a belé írható körének sugarának nagysága megegyezik AMB háromszög beírt körének sugaráéval. Fejezzük ki a háromszög oldalaiból a körök sugarának nagyságát.
|
|










 1)+...+(180-
1)+...+(180- 1+
1+

