|
| [1472] Füge | 2011-01-02 14:08:50 |
 Én deriváltam a parabola egyenletét (mert y=ax2+bx+c alakú volt), és azt tettem egyenlővé a kapott meredekséggel, onnan számoltam pontot, majd m(x-x0)=y-y0 A feladat többi részével nem volt gond, csak azon filóztam, hogy kell-e bizonyítás, vagy sem :)
|
|
| [1471] lorantfy | 2011-01-02 13:37:38 |
 Szerintem itt nem kell a bizonyítással vacakolni. Ezt ismertnem vesszük. Felteszem, hogy a P pont az O középpontú körön belül van:
1. Felirjuk P ponton átmenő OP normálvektorú egyenes egyenletét.
2. y-ra rendezzük, hogy meglegyen a meredeksége=m.
3. A parabola érintője y=mx+b alakú, b paraméter.
4. Egyenletrendszer a parabola egyenletével. Behelyettesítve másodfokú egyenlet. Mivel érintőről van szó a diszkrimináns = 0. Ebből megvan b, tehát ismerjül az érintő egyenletét.
5. Felírjuk az OP egyenes egyenletét.
6. OP metszéspontja az érintővel, egyenletrsndszer: Q
7. PQ távolság.
8. Parabola egyenletéből kiolvasni a F pontot
9. Origó F távolsága.
|
| Előzmény: [1466] Füge, 2010-12-30 23:06:03 |
|
| [1470] Füge | 2011-01-02 13:20:29 |
 Igen én is így indultam neki a feladatnak, csak másodfokú egyenlet rendszer, Viéte-formula, deriválás... azért kérdeztem, hátha van szebb megoldás. Abban igazad van, hogy elfelejtettem mondani, hogy a pont a körön belül van, elnézést. Ez egy próbaérettségi feladatsorból az egyik feladat, és gondolom az első két rész kevés volt még ahhoz, hogy 16 pontot adjanak rá, ezért raktak be egy ilyen részfeladatot, hogy ismered-e a koordinátatengelyekkel párhuzamos vezéregyenesű/tengelyű parabola általános egyenletét.
|
|
| [1469] HoA | 2011-01-02 10:34:18 |
 Az origó említéséből arra következtetek, hogy ezt koordináta-geometriai feladatnak szánták. Az alakzatok tehát koordinátáikkal ill. egyenleteikkel adottak. Ekkor az is elképzelhető, a feladatkitűző arra gondolt, a P ponton átmenő legrövidebb húr meghatározásához írjuk fel a P-n áthaladó általános egyenes egyenletét m iránytangensével paraméterezve, számítsuk ki a körrel alkotott metszéspontok koordinátáit és keressük meg, e két pont távolsága melyik m-re lesz a legkisebb. ( Azt talán illett volna közölni, hogy P a körön belüli pont. )
Amit nem értek: hogy jön a harmadik kérdés az első kettőhöz? Ha adott a parabola, akkor fókusza, és így annak origótól mért távolsága is "adott" ( kiszámítható), függetlenül attól, hogy veszek-e fel egyáltalán még kört meg pontot a síkban. Ettől persze a feladat még korrekt.
|
| Előzmény: [1466] Füge, 2010-12-30 23:06:03 |
|
| [1468] Füge | 2010-12-30 23:11:42 |
 Érettségin kétlem, hogy megkérnek majd, úgyhogy marad az említés :)
|
|
| [1467] Nánási József | 2010-12-30 23:09:20 |
 Ez a Geometria 1-ben vagy 2-ben is benne van... //nekem is aktuális feladat volt nem rég
Nálunk kellett említés szerűen mondani, hogy az a legrövidebb, csak aztán meglettem kérve, hogy bizonyítsam be a táblánál.
|
|
| [1466] Füge | 2010-12-30 23:06:03 |
 Köszönöm a gyors választ. A feladat az volt, hogy adott egy parabola egy kör és egy pont. A parabola azon érintőjét keressük ami párhuzamos a P ponton átmenő legrövidebb húrral(6 pont), milyen messze van a P ponttól(5 pont) és mekkora a parabola fókuszpontjának távolsága az origótól(5 pont). Elképzelhető, hogy kell ez a bizonyítás a feladathoz, vagy elég lehet annyi, hogy triviális? Esetleg, egy egy mondatos indoklás?
|
|
| [1465] Nánási József | 2010-12-30 22:47:46 |
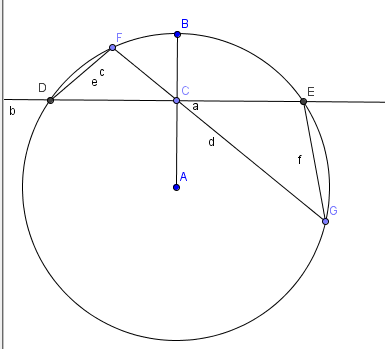
 Legyen ACD szög derékszög, ekkor DC és CE egyenlő (DE húrja a körnek)(mostantól x jelölöm)
Legyen CF y, míg CG z-vel jelölve.
DCF szög és ECG szög egyenlő, mert csúcsszögek.
DFG és DEG szögek egyenlőek, mivel azonos ívhez tartozó kerületi szögek, azaz DFC és CEG minden szöge megegyezik, így hasonlóak.
Hasonlóság miatt:
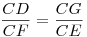
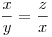
Mivel ezek valós szakaszok, emiatt az egyenletet átrendezve:
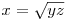
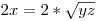
Tegyük fel hogy y+z kisebb mint 2x.
2x helyére írjuk be y+z-t, illetve az egyenletnek vegyük a kettővel képzett hányadosát. Ekkor azt várjuk, hogy hogy az egyenlet bal oldala kisebb lesz mint a jobb.
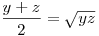
A számtani mértani közép tulajdonsága miatt, az egyenlet bal oldala nagyobb mint ajobb (S>M)
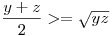
Itt tehát ellentmondás áll fent, azaz y+z>=2x.
Az egyenlet akkor és csak akkor teljesül, ha y=z, amikor pedig a merőleges húrt kapjuk vissza.
Tehát a legrövidebb húr a sugárra merőleges.
|
 |
|
| [1464] Füge | 2010-12-30 22:09:02 |
 Üdv!
Egy eléggé elemi kérdésem lenne, amire nem tudtam választ keríteni. Adott körben adott ponton átmenő húrok közül melyik a legrövidebb? Illetve az triviális, hogy a húrra merőleges, de bizonyítani nem nagyon tudtam.
(Megjegyzés: Próbaérettségi feladat emelt szint, II. rész, a feladat a,b,c, részből áll, és ezt az a, rész felénél kellene használni, szóval nem lenne rossz valami rövidebb bizonyítás)
|
|
| [1463] BohnerGéza | 2010-11-17 11:29:48 |
 Másik megoldást kaphatunk, ha észrevesszük az A*B1B2 és A*C1C2 háromszögek hasonlóságát. Területet is fölhasználva megadhatjuk, hogy AA* metszéspontja milyen osztóviszonyt ad BC-n. ...
|
| Előzmény: [1462] BohnerGéza, 2010-11-17 11:23:56 |
|
| [1462] BohnerGéza | 2010-11-17 11:23:56 |
 Az idei Kürschák-verseny 2. feladata: Az ABC háromszög AB oldalának belsejében adottak a C1 és C2 pontok, a BC oldal belsejében az A1 és A2 pontok, végül a CA oldal belsejében a B1 és B2 pontok úgy, hogy AC1<AC2, BA1<BA2, és CB1<CB2 teljesül.
Az AB1C1 és AB2C2 körök A-tól különböző metszéspontját jelölje A*, a BC1A1 és BC2A2 körök B-től különböző metszéspontja legyen B*, végül a CA1B1 és CA2B2 körök C-től különböző metszéspontját nevezzük C*-nak.
Mutassuk meg, hogy az AA*, BB* és CC* egyenesek egy ponton mennek át!
|
 |
|
| [1461] Tóbi | 2010-10-27 16:15:30 |
 Kiszámolni nem nehéz, bár azt nem látom miért igaz. Feltehető, hogy a henger tengelye a z tengely, sugara r, míg a paraboloidot az xy síktól és a P=(a,0,b) ponttól egyenlő távol lévő pontok alkotják. Ekkor ha (x,y,z) mindkét alakzatnak eleme:
x2+y2=r2
(x-a)2+y2+(b-z)2=z2
Kivonva a két sort egymásból:
2ax+2bz=a2+b2+r2
Tehát a metszet benne van a fenti síkban.
|
| Előzmény: [1460] HoA, 2010-10-27 10:56:11 |
|
| [1460] HoA | 2010-10-27 10:56:11 |
 Rég nem volt feladat. Az alábbiról sem állítom, hogy új ( RóbertGida biztos tud forrást is hozzá ) , nekem is egy korábbi KöMaL feladat kapcsán jutott eszembe:
Bizonyítsuk be, hogy egymással párhuzamos tengelyű forgási paraboloid és végtelen körhenger metszésvonala síkgörbe.
|
|
| [1459] Lóczi Lajos | 2010-10-03 22:54:39 |
 Képlet, zárt alak, stb. akkor lesz az inverzre, ha valaki bevezet erre vagy az ehhez hasonló függvényre egy új nevet és kiszámolja néhány tulajdonságát.
Az elmúlt évszázadokban ez sok tucatszor megtörtént a fontosnak bizonyult függvények esetén, amelyek nem voltak "elemi függvények". Így született meg a "speciális függvények" azóta is egyre bővülő osztálya. Rögtön világossá válik a helyzet, ha vetsz egy pillantást egy ilyen gyűjteményre, pl. itt. Ezen függvények mindegyikét hívhatod "zárt alaknak". A hozzászólásodban említett függvény inverze is zárt alakú lesz, ha elnevezed pl. ojozso(x)-nek.
|
| Előzmény: [1458] ojozso, 2010-10-03 20:17:28 |
|
| [1458] ojozso | 2010-10-03 20:17:28 |
 Köszönöm mindenkinek a segítséget a 172. feldattal kapcsolatban, egyik szemem sír (nincs elemi megoldás), a másik nevet (nem a tudásom kopott meg 30 évvel az érettségi után...). A feladatot nem én, hanem az "Élet" alkotta: egy hangszerkesztő programban a megrajzolt körív szerint kellene a dinamikát (ennek révén az átlagos hangosságot) változtatni. A változtatás mértéke nyilván valamilyen arányosságban áll a körszelet területével: minél "domborúbb" (kisebb sugarú a körív), annál nagyobb lesz az átlagos hangosság-növelés (és dinamika-csökkentés). Az elérni kívánt és az aktuális hangosság-szint hányadosa adott, ennek megfelelően adott a körszelet területe is; ebből kellene a körív sugarát meghatározni, majd ha ez megvan, a körív tetszőleges pontjának koordinátáit meghatározni (ami viszont már könnyű). Abban egyetérthetünk, hogy PONTOSAN az adott körszelet területét egy, és csakis egy bizonyos sugarú körív biztosítja: a terület és a sugár között szigorúan monoton megfeleltetés van: minél nagyobb a sugár, annál kisebb a terület. Határértékkel: ha a sugár tart végtelenhez, a terület tart 0-hoz. Képlet hiányában a sugarat próbálkozásokkal be fogom tudni "lőni" tetszőleges pontossággal a területhez (végülis számítógépes program fogja számolgatni), csak elegánsabbnak gondoltam a képlet alkalmazását, ezért tettem fel a feladatot.
A matematikához visszatérve, úgy gondolom, előbb-utóbb lesz zárt alak az általam felvetett és az ahhoz hasonló (pl. a későbbiekben említett) függvény INVERZÉRE is, de az NEM elemi módszerekkel lesz levezetve!
|
|
| [1457] Lóczi Lajos | 2010-10-03 15:28:45 |
 Ahogyan már el is hangzott, ezek olyan elemi függvények, amelyeknek az inverze nem elemi függvény. Persze a függvény is és az inverze is hatványsorba fejthető például, amiből közelítő megoldásokat ki lehet olvasni.
|
| Előzmény: [1455] HoA, 2010-10-01 23:02:52 |
|
| [1456] jonas | 2010-10-02 17:18:57 |
 Az én kedvenc példám az efféle egyenletekre az, amikor egy ellipszispályán keringő bolygó helyét akarjuk megadni az idő függvényében. Ez általában egy sinx=ax+b típusú egyenletre vezet, aminek elemi függvényekkel nem lehet megtalálni a megoldását. A helyből az időt viszont vissza lehet számolni csak elemi függvényekkel.
|
|
| [1455] HoA | 2010-10-01 23:02:52 |
 Kedves matematikus fórum látogatók! Igen, azt hiszem itt az a kérdés, van-e valamilyen fogalom az ilyen értelemben nem invertálhazó függvényekre. Vagyis amikor y kifejezhető zárt alakban x függvényeként, például
y=x+sin(x)
, de x nem adható meg zárt alakban y függvényeként.
|
| Előzmény: [1454] Gubbubu, 2010-10-01 22:05:05 |
|
| [1454] Gubbubu | 2010-10-01 22:05:05 |
 Nem is az a fő baj, hogy transzcendens (tkp. az abszolútértékes egyenletek is transzcendensek, mégis szépen meg lehet őket oldani :-). Talán érdemes lenne a Wikipédiában megnézni az implicitfüggvény-tétel c. szócikket, az én ismerettáramban ez a legközelebbi fogalom, aminek egyáltalán köze lehet a feladatodhoz, bár hogy alkalmazható-e ... ? Amúgy a probléma maga szép, amit feladtál. :-)
|
| Előzmény: [1453] nadorp, 2010-10-01 12:15:55 |
|
| [1453] nadorp | 2010-10-01 12:15:55 |
 A végeredményed jó, de ebből r-t szerintem nem lehet kifejezni, mert ez egy transzcendens egyenlet. ( hasonlóan pld. az x=3sinx egyenlethez). Csak közelítő megoldás van.
|
| Előzmény: [1452] ojozso, 2010-09-29 20:20:00 |
|
| [1452] ojozso | 2010-09-29 20:20:00 |
 Köszi a választ!
Én is próbálkoztam a megoldással, mielőtt feltettem a Fórumra a feladatot, csak nem akartam befolyásolni vele senkit.
Most leírom, meddig jutottam el.
A körszelet területe (t): Tkorszelet=Tkorcikk-TQOCharomszog.
A HÁROMSZÖG TERÜLETE:
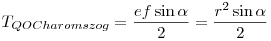 , mivel e=f=r , mivel e=f=r
OFQ derékszögű háromszögben (F az OC szakasz felezőpontja) OQF szög  fele. Szinusz definíciója alapján: fele. Szinusz definíciója alapján:
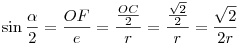 , mivel , mivel 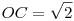 (OC szakasz egységnyi befogókkal rendelkező háromszög átfogója). (OC szakasz egységnyi befogókkal rendelkező háromszög átfogója).
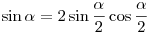 . (Kétszeres szög szinusza). A . (Kétszeres szög szinusza). A 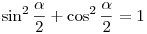 azonosságból: azonosságból: 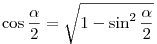 , melyet behelyettesítve kapjuk: , melyet behelyettesítve kapjuk:
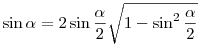 . Beírva . Beírva 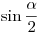 -re kapott -re kapott 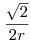 értéket: értéket:
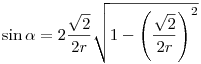 . Egyszerűbb alakra hozva megkapjuk, hogy . Egyszerűbb alakra hozva megkapjuk, hogy 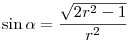
A háromszög területe tehát:
| (1) | 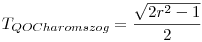 |
A KÖRCIKK TERÜLETE:
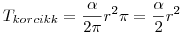 ( ( radiánban.), vagyis: radiánban.), vagyis:
| (2) | 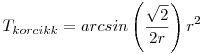 |
A KÖRSZELET TERÜLETE:
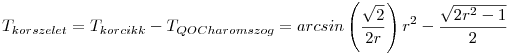
És itt a végállomás! Fogalmam sincs, hogyan lehetne ebből r-et kifejezni, már csak azért sem, mert r az arcsin argumentumában is szerepel és nem tudom, hogyan lehet onnan kihozni.
Innentől kéne segítség. Ráadásul abban sem vagyok biztos, hogy eredményem ekvivalens-e a Tieddel.
|
 |
| Előzmény: [1450] Gubbubu, 2010-09-28 12:19:53 |
|
|
| [1450] Gubbubu | 2010-09-28 12:19:53 |
 Az első feladatra nekem az 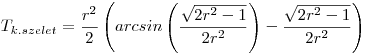
A megoldás leírásához szükséges időm most túl kevés, estefelé vagy pár nap múlva talán; így a képzeletbeli margón marad :-).
Szükséges lenne természetesen az ért. tartományok vizsgálata is, továbbá esetleges geometriai diszkusszió. Nagy vonalakban az történt, hogy kiszámolod a körcikk területét (ez egyszerű egyenes arányosság), majd az ún. trigonometrikus területképlettel az OAC háromszögét, és kivonod a kettőt egymásból. Ezután kifejezed az omega szöget az r segítségével (ehhez ügyeskedni kell az addíciós tételekkel), így eltüntetvén az omegát a képletből (opcionális, az arcsin-elt kifejezés egyébként maga a szinusz omega).
|
| Előzmény: [1449] ojozso, 2010-09-27 18:49:48 |
|
| [1449] ojozso | 2010-09-27 18:49:48 |
 Sziasztok!
Új vagyok itt és adódott egy probléma, melyen nem tudok túljutni, de Nektek bizonyára menni fog... Tehát:
172. feladat
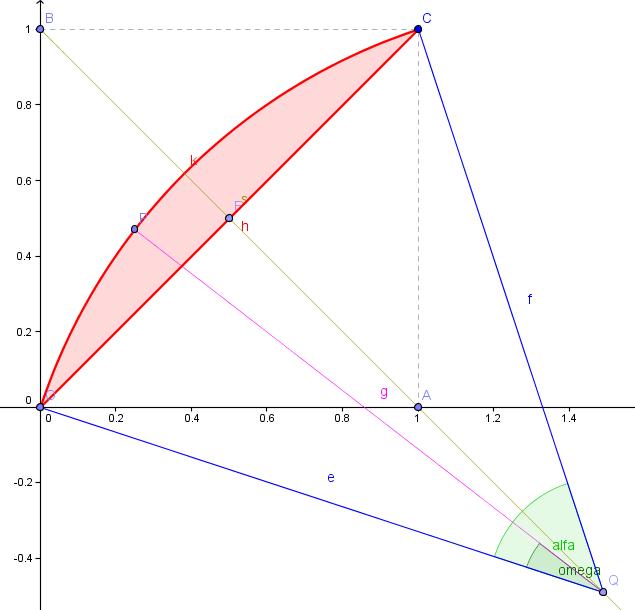
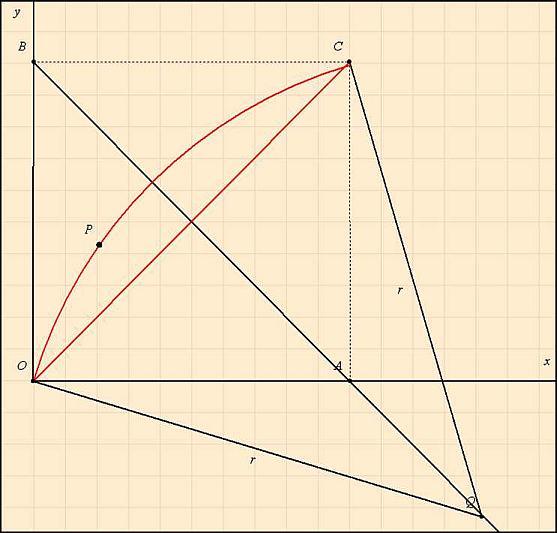
Jelöljük O-val az origót (0;0), A-val az (1;0), B-vel a (0;1) és C-vel az (1;1) pontokat. Az AB szakasz A ponton túli meghosszabításával kapott félegyenesen AB szakaszon kívül vegyünk fel egy tetszőleges Q (u;v) pontot. QO=QC=r sugárral rajzoljuk fel a Q középpontú OC körívet. Ezen a köríven vegyünk fel egy tetszőleges P (x;y) pontot. Az OC szakasz és az OC körív által (pirossal) határolt körszelet területét jelöljük t-vel, az OQP szöget pedig omega-val (QP szakasz sajnos, lemaradt a rajzról.)
Határozzuk meg az adott t területű körszelethez tartozó r sugarat!
Írjuk fel az adott adott t területű körszelethez tartozó körív tetszőleges P pontjának koordinátáit r és omega függvényében!
|
 |
|













 fele. Szinusz definíciója alapján:
fele. Szinusz definíciója alapján: 
