|
| [14] tarcsay | 2004-01-15 15:44:55 |
 Kedves gubbubu!
Ha jól emlékszem, akkor a
http://www.cut-the-knot.org/Generalization/ceva.shtml
oldalon láttam olyan bizonyítást, amit kerestél.
Üdvözlettel,
|
| Előzmény: [13] Gubbubu, 2004-01-14 20:44:15 |
|
| [13] Gubbubu | 2004-01-14 20:44:15 |
 Kedves Fórumosok!
Hónapok óta nyomozok a Ceva-tétel olyan bizonyítása után, amely nem használja fel, lehetőleg implicit módon sem, a terület fogalmát (mint ahogy pl. Coxeter geometriakönyve teszi), hanem mondjuk háromszögek hasonlóságára épít. Ha véletlenül ismer valaki ilyet, nagyon kérem, írja meg, hol található (könyv, webcím stb.)
Köszönettel: G
|
|
| [12] Rácz Béla | 2004-01-14 01:53:28 |
 Variáció a 2. feladatra:
2/b. Legyen egy háromszög Gazsi-egyenese a körülírt és a beírt kör középpontja közti egyenes (ill. az egész sík, ha a háromszög esetleg szabályos). (Gazsi tétele:) BBH a 2. feladatban az Euler szót Gazsira cserélve is igaz a tétel!
|
| Előzmény: [3] Csillag, 2003-12-19 19:38:04 |
|
| [11] Hajba Károly | 2004-01-14 00:36:02 |
 Válasz a 4. feladatra:
Kedves Csimby! Először azt hittem, hogy blöf vagy valamiféle végtelennel történő játékkal lehet megoldani, de nem. Belémcsapott az isteni szikra és rájöttem a megoldásra.
Nem akarom az esetleg ezen gondolkodók kedvét elvenni, így csak utalok rá és egyben inspirációt adok a még gondolkodók részére: 12 idom, s ebből akár a fele is megfelel a feltételeknek, de ugyanezen elemekkel a "hagyományos" módon is ki lehet rakni. Sőt 6*n elemmel is megoldható.
HK
|
| Előzmény: [10] Csimby, 2004-01-12 21:54:12 |
|
| [10] Csimby | 2004-01-12 21:54:12 |
 4.feladat: Bontsunk fel egy kört egybevágó síkidomokra úgy, hogy legalább az egyik darab ne tartalmazza a kör középpontját, még határán sem.
|
|
| [9] Hajba Károly | 2004-01-10 00:26:54 |
 3. feladat
Mekkora méretű lehet az a legkisebb négyzet alakú mező, melybe 12 db egységnyi átmérőjű kört be tudunk még átfedés nélkül illeszteni?
HK
|
|
| [8] Hajba Károly | 2004-01-05 14:12:58 |
 2. feladat
Vegyünk egy 1,895/18,95 méretű mezőt és próbáljunk benne minél több 1,0/1,0 méretű lapocskát átfedés nélkül elhelyezni.
Vajon mennyit lehet?
Hajba Károly
|
|
|
| [6] lorantfy | 2003-12-20 21:55:41 |
 Kedves Zanaty!
Kösz a gyors segítséget! Próbáltam már GIF-ben de rosszul választhattam meg a háttérszínt és konvártálás után pöttyös lett, így elvetettem. Most megpróbáltam átlátszó háttérrel és szuper. Mégegyszer kösz!
Üdv! L.
|
| Előzmény: [5] Zanaty, 2003-12-20 18:06:19 |
|
| [5] Zanaty | 2003-12-20 18:06:19 |
 Kedves László!
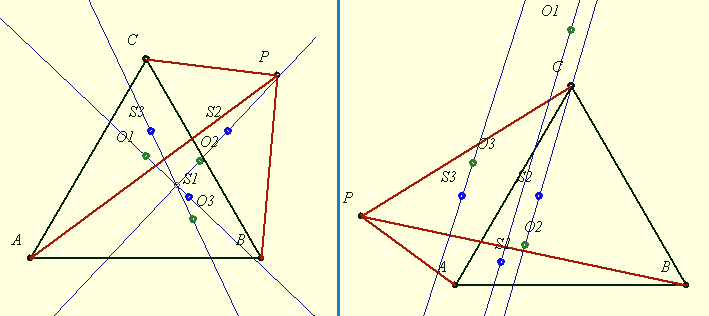
Javaslom neked a GIF formátumot (CompuServe Graphics Interchange). Ez a kép az ábrád rekonstruciója, remélem segítettem.
|
 |
|
| [4] lorantfy | 2003-12-20 12:28:49 |
 Kedves Csillag!
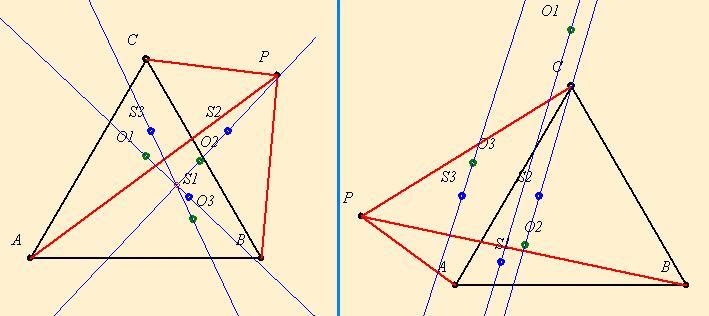
Gratulálok a tételedhez! És, hogy több megoldó legyen, gyorsan egy kis szemléltetés. Nagyon jó játék ez az Euklides program. Ez a két ábra kb. 3 perc alatt megvan. Ha valaki le akarja tölteni, a www.euklides.hu/hun/euklides.htm címen megtalálja. (Sajnos a vonalak kicsit elmosódottak, mivel a méret miatt JPG-be kell konvertálnom. Ha valaki tudd jobb módszert szóljon!)
|
 |
| Előzmény: [3] Csillag, 2003-12-19 19:38:04 |
|
| [3] Csillag | 2003-12-19 19:38:04 |
 Üdv Mindenkinek!
A most következő feladat megoldásáért jutalom jár!!! A megoldásokat e-mailben várom! Két díj lesz: 1. gyorsasági, 2. szépségdíj(ehhez határidő: március 31.). A nyertesekkel megbeszéljük, hogy milyen csokit szeretnek...
2. feladat: (Gáti Beatrix tétele:) Adott a síkon egy szabályos háromszög(ABC) és egy tetszőleges P pont. Bizonyítandó, hogy az ABP, BCP, CAP háromszögek Euler-egyenesei egy ponton mennek át, vagy párhuzamosak.
GB
|
|
|
| [1] Csillag | 2003-12-18 21:17:42 |
 Üdv Mindenkinek!
Ez a téma azért készült, hogy a geometria érdekes részeiről, tételeiről megosszuk élményeinket. Vágjunk bele:
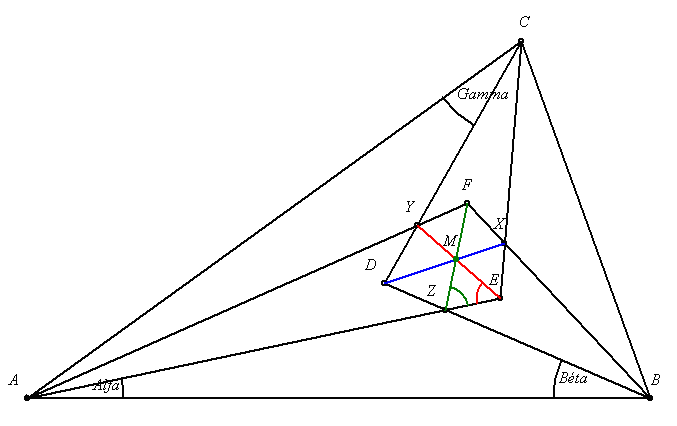
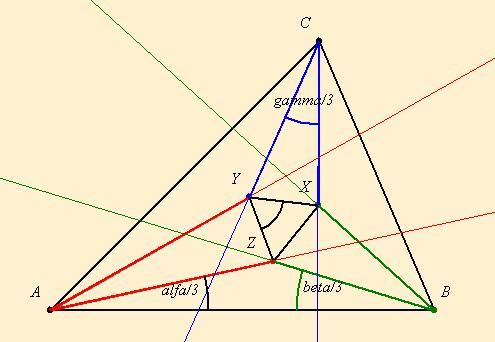
1. feladat: Morley tétele: Egy tetszőleges háromszög szögeit az AY, AZ; BZ, BX; CX, CY egyenesek 3-3 egyenlő részre osztják. Bizonyítsuk be, hogy az XYZ háromszög szabályos.
GB
|
|







 szögeinek harmadai
szögeinek harmadai  ,
, ,
, .Mivel 3
.Mivel 3 =90o-
=90o-