|
| [1522] HoA | 2011-12-20 17:31:48 |
 Vázlat: Javaslom a párhuzamos szelők - egyik - tételének egy "megfordítását" : párhuzamosok közötti párhuzamos szakaszok egyenlőek --> párhuzamosok közötti egyenlő szakaszok vagy párhuzamosak vagy ugyanakkora szöget zárnak be a párhuzamosakkal. Ebből adódik, hogy az átlók felezik egymást, és mivel egyenlőek a hat csúcs az átlók metszéspontjától félátlónyi távolságra van, tehát egy körön vannak.
|
| Előzmény: [1521] Erika95, 2011-12-20 17:01:06 |
|
| [1521] Erika95 | 2011-12-20 17:01:06 |
 Sziasztok! A segítségeteket szeretném kérni az alábbi feladat megoldásában: Bizonyítsuk be,hogy egy hatszög szemben fekvő oldalai párhuzamosak és a szembenfekvő csúcsokat összekötő átlók egyenlőek egymással, akkor a hatszög csúcsai egy körön vannak. A hatszög nem biztos hogy szabályos hatszög.
Köszönöm szépen.
|
|
|
|
| [1518] Tatanka Yotanka | 2011-12-12 10:05:37 |
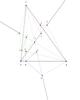 Kedves Sirpi! Kérdésed, hogy "miért a szögfelezőkre?" teljesen jogos. A DEF háromszög (és a hasonló eljárással létrehozott GHI, JKL háromszögek is) mindig hasonló az ABC háromszöghöz, nem kell, hogy a B,C pontokból az A-ból szögfelezőre bocsássunk merőlegest, elegendő egy A-ból induló, és a szemközti oldalt metsző egyenes, sőt, akár a szemközti oldallal párhuzamos is lehet. A szögfelezős változat nyilván egyszerűbb, a hasonlóság arányát könnyebb fölírni.
|
|
| [1517] Tatanka Yotanka | 2011-12-12 09:09:58 |
 Bocsánat, egy feltételt kihagytam a fölvetett feladatból. Az A pontbeli belső szögfelezőre a B és C pontokból bocsátunk merőlegest. Hiába, kezdő vagyok.
|
|
|
| [1515] Tatanka Yotanka | 2011-12-12 07:00:59 |
 Üdvözlet mindenkinek! Új hozzászólóként szeretnék egy feladatot, illetve problémát fölvetni: Az ABC háromszög A csúcsából bocsássunk merőlegest a szemben levő oldalra, a merőleges talppontja legyen D. Ezután állítsunk merőlegeseket az A-ból induló belső szögfelezőkre, a talppontok itt E és F. Hasonlóképpen szerkesztjük meg a C és B pontokból kiindulva a GHI és JKL háromszögeket. Az könnyen igazolható, hogy DEF, GHI és JKL mindegyike hasonló az ABC háromszöghöz, de ezen háromszögek területének összege lehet-e pl. az ABC háromszög területével egyenlő, annak a fele stb., illetve mennyi a három terület összegének maximuma?
|
|
| [1514] Lajos bácsi | 2011-12-09 18:04:34 |
 Na végre, azt hittem nem lesznek válaszok, de úgy látom, nem sok ember képzelőerejét mozgatta meg a felvetett kérdés.
|
|
|
|
| [1511] Lajos bácsi | 2011-12-07 15:03:45 |
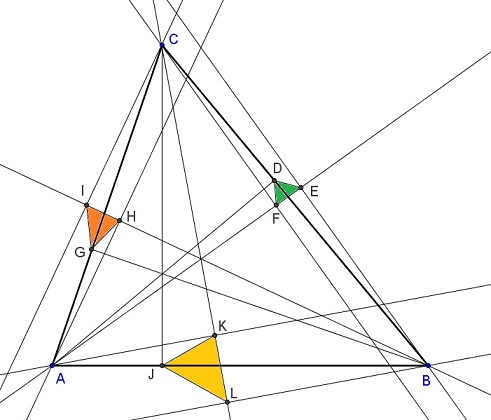
 Rajzoljátok vagy írjátok le azt a 3 dimenziós tárgyat, melyet különbözőképpen elforgatva és megvilágítva az ábrán látható árnyképeket produkálná.
|
 |
|
| [1510] Vonka Vilmos Úr | 2011-06-18 18:18:56 |
 Következzen inkább csak egy kis útmutatás, remélem, utána könnyebb lesz megoldanod a feladatot.
1. Legyen a szabályos n-szög középpontja O, két szomszédos csúcsa A és B. A szabályos n-szög helyett vizsgáljuk az ABO egyenlő szárú háromszöget. Ebben a háromszögben milyen adat R és milyen adat r? Ha ezt meggondoltad, akkor legyen F az AB szakasz felezőpontja, és vizsgáljuk (például) az AFO háromszöget. Ez a háromszög derékszögű (miért?), így bármelyik oldalát könnyedén kiszámíthatjuk szögfüggvények segítségével. Ha már látod, hogy az ABO háromszög milyen adatai R és r, akkor ennek a háromszögnek az oldalhosszai elvezetnek a R-re és r-re vonatkozó formulákhoz.
A terület kiszámításához is elég az ABO háromszög területét meghatároznod. (Hányszorosa ennek a szabályos n-szög területe?)
2. Az előző formulákba n=8-at kell behelyettesíteni. Ehhez pi/8 szögfüggvényeinek pontos értékére van szükséged. Ez egy nevezetes szög (45 fok) fele, ezért a félszögek szögfüggvényeire vonatkozó képletek (nézz utána!) alapján kaphatod meg a szükséges formulákat.
3. Itt szintén az 1. feladatban nyert képletekbe kell behelyettesíteni. A szögfüggvények pontos értékei csak n=5 és n=10 esetén nem annyira ismertek. Ezek közül nyilván elég az egyiket kiszámítani. (A másik a kétszeres szögre vagy félszögre vonatkozó képletek alapján adódik.) n=10 esetén például a 18 fokos szög szögfüggvényeire lesz szükség. Az erre vonatkozó számításokhoz segítség: annak az egyenlő szárú háromszögnek, amelynek alapon nyugvó szögei 72 fokosak, az alapja és a szára az aranymetszés szerint aránylik egymáshoz, azaz arányuk (gyök(5)-1)/2.
|
| Előzmény: [1509] virágzótisza, 2011-06-18 14:50:10 |
|
| [1508] Maga Péter | 2011-06-18 17:28:48 |
 Innen ilyenekért nem fognak kitiltani (feltéve, hogy nem valamely aktív KöMaL-feladathoz kapcsolódik a kérdésed:)), tudunk ,,ilyesmiről'' beszélgetni.
A feladatokat nem lövöm le. Nem tudom, hogy van-e egyáltalán olyan látogatója a fórumnak, aki még életében nem gondolta meg az ismertetett formulákat...
Javaslom az oldalon található TeX tanfolyam elvégzését, már ezeket a bevezető képleteket is kellemetlen ebben a formában olvasni.
|
| Előzmény: [1509] virágzótisza, 2011-06-18 14:50:10 |
|
| [1509] virágzótisza | 2011-06-18 14:50:10 |
 Sziasztok! Ahányszor csak kérdezek, vagy nicket regisztrálok az index fórumon, annyiszor kitörlik kérdésemet és kitiltanak. Most a matematika-elsősegély topikból tiltottak ki az alábbi kérdések miatt.
1. Bizonyítsuk be, hogy az a oldalhosszúságú szabályos n szög köré írt kör sugara R=a/(2sin(pi/n)), beírt kör sugara r=a/2tg(pi/n) terülte S=nar/2 2. Mutassuk meg 1. felhasználásával, hogy a szabályos nyolcszögre R=agyök(1+(gyök2)/2), r=a(1+gyök(2))/2, S=2a**2(1+gyök(2)) 3. Töltse ki az alábbi táblázatot: n, R,r,S, ahol n =3,4,5,6,10 (A fenti alakhoz hasonlóan adja meg a formulákat!)
Tudunk itt ilyesmiről beszélgetni?
|
|
|
|
|
|
|
|
| [1501] gubanc | 2011-04-19 12:03:38 |
 A 2)-höz: Így egyszerűbb volt a számítás, mert meg lehetett spórolni a 4R-es szorzó többszöri leírását.
Köszönöm a részletes "helyretételt". A dorgálást megérdemlem, hiszen egy félreértés miatt árnyékra vetődtem és előbb írtam, mint gondolkoztam. Több tanulság van, az egyik, hogy késő éjszaka, hullafáradtan nem szabad matekoznom ... .
Nem állt szándékomban megbántani, főleg nem Téged, hiszen korábban és most is nagy élvezettel olvastam, olvasom frappáns levezetéseidet, megoldásaidat. Elnézést, ha megbántottalak volna. Üdv: gubanc
|
| Előzmény: [1500] nadorp, 2011-04-19 10:34:47 |
|
| [1500] nadorp | 2011-04-19 10:34:47 |
 Az "álbizonyítás" megjegyzésed kissé erős...De ettől függetlenül:
1). Idézet tőlem: "nálam minden x,y,z távolságra van megoldás ( az más kérdés, hogy ez szerkeszthető-e)"
Ezzel azt a félrértést szeretném eloszlatni, hogy én csak a megoldhatóságot ( diszkussziót ) vizsgáltam, nem a geometriai szerkeszthőséget.
2.) Az eredeti feladat szerint: Szerkesszük meg a háromszöget, ha adottak a beírt kör középpontjának a csúcsoktól mért távolságai.
Nem értem, minek kell feltenni, hogy R=1/4. Adott három független adat, szerkesszük meg a háromszöget ( felejtsd most el a hasonlóságot)
3.) "A (*) tartományon kívül eső szögek nem adnak megoldást."
Ez értelmetlen, mert a (*) tartományba nem szögek, hanem szakaszok hosszai esnek.
4.)"A leírtak következménye: az általad előállított f függvény a t = 0 helyen nincs értelmezve, hiszen  > 0 egyben > 0 egyben  > 0-t is jelenti" > 0-t is jelenti"
Már dehogy nincs értelmezve a t=0 és t=1 helyen, félreértésben vagy. Az, hogy megoldásként csak 0 és 1 közti megoldást fogadunk el, attól még a függvény értelmezve van a végpontokban és a Bolzano-tétel is használható rá. ( Így keletkeznek a "Híres álcáfolatok" ).
Fordítva gondolkozzál, a Bolzano-tétel csak egy eszköz. Az egyenletrendszer megoldásából adódik, hogy ha ennek a függvénynek van (0;1)-beli zéróhelye, akkor az megadja 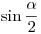 értékét. A Bolzano-tétel ( vagy általában az, hogy zárt intervallumon folytonos függvény tetszőleges két felvett értéke közti értéket is felvesz) csak biztosítja a gyök létezését. A 0 sugarú körrel való "bűvészkedés" helyett pedig tekintsd az f függvényt az [ értékét. A Bolzano-tétel ( vagy általában az, hogy zárt intervallumon folytonos függvény tetszőleges két felvett értéke közti értéket is felvesz) csak biztosítja a gyök létezését. A 0 sugarú körrel való "bűvészkedés" helyett pedig tekintsd az f függvényt az [ ;1- ;1- ] intervallumon, ahol ] intervallumon, ahol  olyan kicsi pozitív szám, hogy f( olyan kicsi pozitív szám, hogy f( )<0 és f(1- )<0 és f(1- )>0 és egyből megszűnnek az értelmezésbel gondjaid. )>0 és egyből megszűnnek az értelmezésbel gondjaid.
5.) "Egyébként jó, hogy ez a probléma is felmerült, mert roppant tanulságosnak tartom"
Akkor tanulj belőle.
|
| Előzmény: [1495] gubanc, 2011-04-19 02:13:48 |
|
| [1499] Kemény Legény | 2011-04-19 10:11:38 |
 "Azt mondod, hogy ha egy racionális együtthatós harmadfokú egyenletnek nincs racionális gyöke, akkor a gyökei nem szerkeszthetőek?"
Igen.
Arra, hogy egy szám nem szerkeszthető, elégséges feltételt ad az, hogy a minimálpolinomjának a foka nem kettőhatvány. Márpedig azok a rac. együtthatós harmadfokú polinomok, amiknek nincs rac. gyökük, irreducibilisek.
|
| Előzmény: [1498] jonas, 2011-04-19 10:02:13 |
|










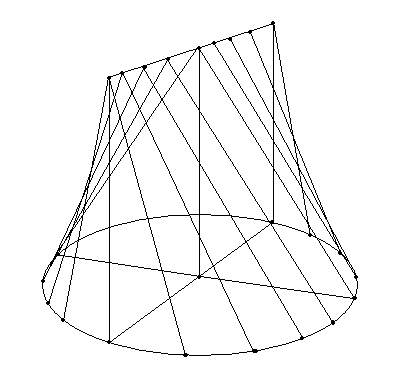





 60o feltétel két okból sem lehet a diszkusszió része. Egyrészt, mert a diszkusszió csak a kezdetben adott x,y,z mennyiségeket tartalmazhatja. Másrészt mert felesleges feltétel, ugyanis az x
60o feltétel két okból sem lehet a diszkusszió része. Egyrészt, mert a diszkusszió csak a kezdetben adott x,y,z mennyiségeket tartalmazhatja. Másrészt mert felesleges feltétel, ugyanis az x y és x
y és x > 0 egyben
> 0 egyben  ;1-
;1-