|
| [1554] Lóczi Lajos | 2012-05-22 12:45:05 |
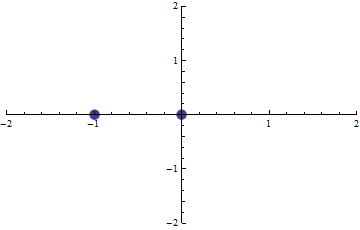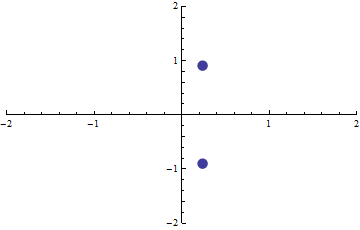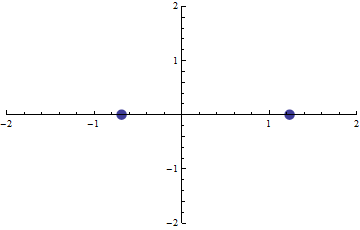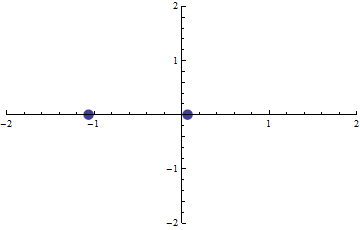
 180. feladat. Valamely p és q valós számok esetén tekintsük az f(x):=x2+px+q polinomot.
A (p,q) pont a síkon fussa be az origó középpontú egységsugarú körvonal peremét. Ekkor az f(x)=0 egyenlet gyökei a (komplex) síkon szintén körbejárnak.
Milyen alakzat áll elő így a gyökök mozgása során? Mutassuk meg, hogy
-- a (komplex) síkon az alakzatot magába foglaló, origó középpontú és minimális sugarú kör sugara 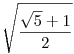 , ,
-- az alakzat területe pl. 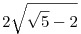 és és 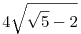 közé esik. közé esik.
|
|
| [1553] BohnerGéza | 2012-05-22 09:26:24 |
 Az alábbi feladat megoldása nem jelent meg a KÖMAL-ban.
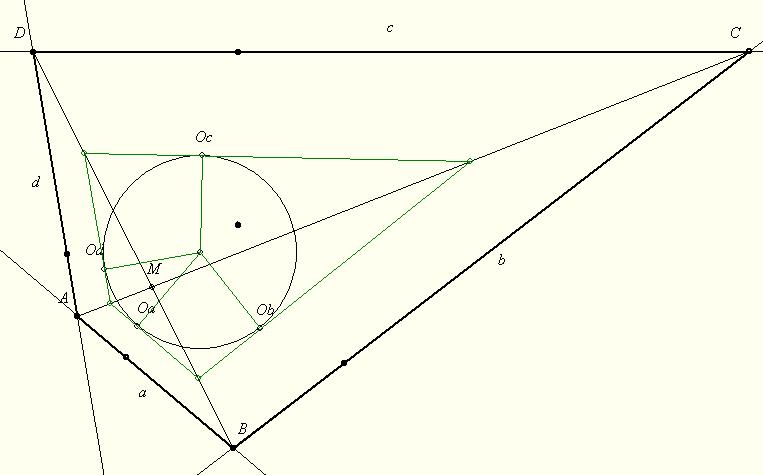
A. 549. Az ABCD érintőnégyszög átlói az M pontban metszik egymást. Mutassuk meg, hogy az ABM, BCM, CDM és DAM háromszögekbe írt körök középpontjai egy körön vannak.
A feladattal kapcsolatban a következő merült föl:
Legyenek a megfelelő középpontok Oa, Ob, Oc és Od. Az új állítás: Az ObOcOd körhöz az Ob-ben és Oc-ben húzott érintők az MC egyenesen metszik egymást. (Ennek bizonyítása valószínűleg az eredeti A. 549. feladattal egyforma nehézségű, vagy nehezebb.)
Viszont annak bizonyítása, hogy ebből az új állításból következik az eredeti, már emberi léptékű.
179. feladat: Bizonyítandó, hogy az új állításból következik az A. 549. feladat állítása.
|
 |
|
| [1552] BohnerGéza | 2012-05-09 11:13:00 |
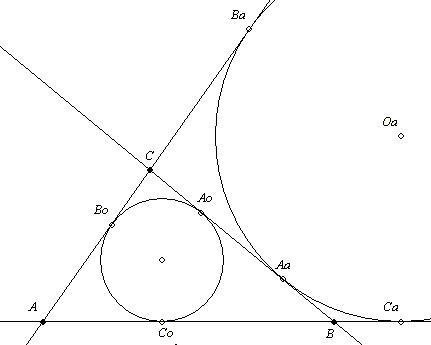
 Maradok a nálam szokásos jelöléseknél, így kevesebb elírás várható.
Az oldalakon az érintési pontokat a szemközti csúcs nagybetűjével és indexekkel jelölöm: a beírt körhöz a 0, az érintőkörökhöz belül érintett oldal (a, b, c) az index.
Külső pontból a körhöz húzott két érintőszakasz hossza megegyezik:
ABo = ACo = x, BCo = BAo = y, CAo = CBo = z.
2(x+y+z)= k (kerület) x+y+z = s (félkerület), ahonnan pl.
x = s-(y+z) = s-a
Magyarul: Csúcstól a beírt körig tartó érintőszakaszt kapjuk, ha a félkerületből levonjuk a szemközti oldalt.
Mivel BCa = BAa, CAa = CBa és ABa = ACa, 2s = AaC+CA+AB+BCa = BaA+ACa.
Tehát ABa = ACa = s. Magyarul: Csúcstól a szemközti hozzáírt körig tartó érintőszakasz hossza a félkerület.
Ezeket tudva beláthatod, hogy kérdésedre a válasz PQ = |b-c|.
Érdekes eredményeket kapsz, ha meghatározod például a következő szakaszok hosszát:
CoCa, CbCa, BCa, BCo, ... (egy oldalegyenesen van két csúcs és 4 érintési pont, bármely kettő távolsága meghatározható.)
Ezek ismerete szerkesztési feladatokban is segíthetnek.
|
 |
| Előzmény: [1550] matekpelducik, 2012-05-08 22:26:30 |
|
|
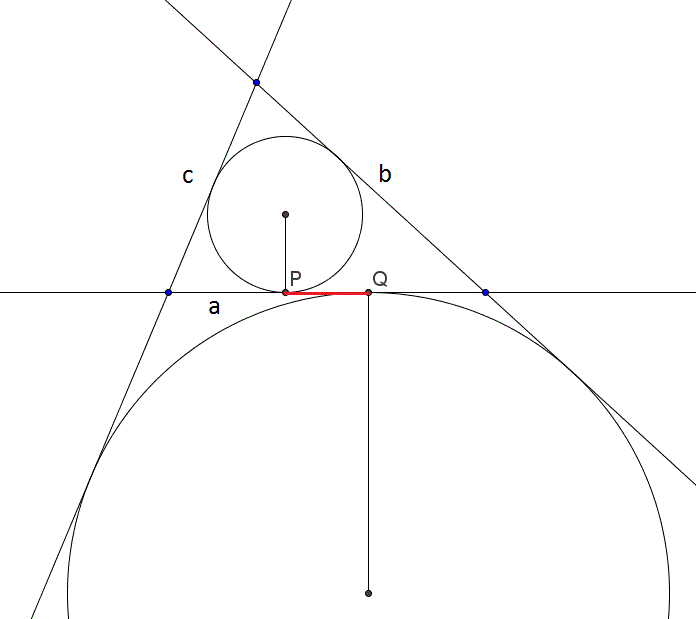
| [1550] matekpelducik | 2012-05-08 22:26:30 |
 Egy háromszög oldalainak hossza a, b és c.Érintse az a hosszúságú oldalt a beírt kör a P,a hozzáírt kör a Q pontban.Fejezzük ki a PQ szakasz hosszát b és c segítségével!
Ehez a feladathoz várnék megoldást :) Előre is köszi (Levezetve)
|
|
|
| [1548] Fálesz Mihály | 2012-05-02 09:58:01 |
 Vannak speciális esetek, amikor egy sokadrendű görbe és egy kör metszéspontja véletlenül mégis szerkeszthető.
Jó lenne egy olyan esetet kipreparálni, amikor a megadott adatok "szépek", de az eredményben valami jól ismert, nem szerkeszthető mennyiség szerepel.
|
| Előzmény: [1547] BohnerGéza, 2012-05-02 02:11:52 |
|
| [1547] BohnerGéza | 2012-05-02 02:11:52 |
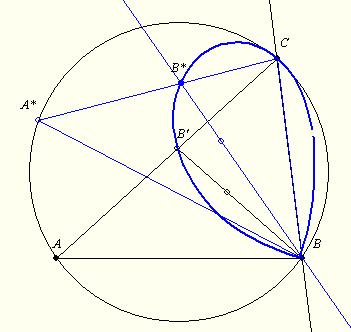
 Egy példa, ahogyan a 178. feladat nem szerkeszthető:
(A BC oldal és a körülírt kör szerkeszthető.)
Tfh az ABC a szerkesztendő háromszög, ekkor a körülírt körén mozgó A* pont és a szerkesztőprogram segítségével kirajzolható az A*BC háromszög B* pontjainak nyomvonala. B* a B-ből induló szögfelező másik vége.
A B* nyomvonala nem másodrendű, így nem szerkeszthető.
A nyomvonal ismeretében B* számára meglenne a két szükséges vonal. (A másik a B kp-ú, az adott szögfelező sugarú kör.)
|
 |
| Előzmény: [1546] Konkoly Lászlóné, 2012-04-24 22:36:53 |
|
| [1546] Konkoly Lászlóné | 2012-04-24 22:36:53 |
 [1546] A 25. feladathoz hasonló szerkesztési feladat:
178.feladat: Szerkesszük meg a háromszöget (vagy mutassuk meg, hogy nem lehetséges), ha adott a háromszög egy oldala (a), a vele szemközti szög (alfa) és nem az alfához, mint a 25. feladatban, hanem egy másik szöghöz (pl. a bétá-hoz) tartozó szögfelező hossza.
|
|
| [1545] HoA | 2012-03-26 14:18:01 |
 "Úgy látom, leszoktunk a feladatok sorszámozása." (áról) Ne tegyük. A 174. volt szerintem az utolsó számozott. Legyen [1531] a 175. , [1537] a 176. és most jöjjön a
177. feladat: Az ABCD húrnégyszög csúcsai által meghatározott ABC, BCD, CDA, DAB háromszögek beírt köreinek középpontja legyen OD , OA , OB , OC . A CD oldalegyenest messe ODOA E-ben, OCOB F-ben . Bizonyítsuk be, hogy ABEF húrnégyszög.
|
| Előzmény: [1531] BohnerGéza, 2011-12-31 01:11:20 |
|
| [1542] Danesz | 2012-03-19 19:18:17 |
 Ja, a kötözködők kedvéért: A definícióban nincs szó síklapokról :P
|
|
| [1541] Danesz | 2012-03-19 19:12:04 |
 A tér a 3-dimenziós euklideszi tér. Ismétlem a definíciót kicsit másképpen: Az A halmaz átdarabolható a B halmazba, ha Az A halmaz felbontható véges sok olyan A1, A2, ..., An diszjunkt halmazra (vagyis az Ai halmazok uniói kiadják A-t), hogy ezeket az Ai halmazokat valamilyen (lehet, hogy minden i-re különböző) mozgással átvihetünk olyan Bi (természetesen szintén n darab) diszjunkt halmazba, hogy a Bi-k egyesítése kiadja B-t. Remélem elég részletes és pontos. Ja, és a mozgás az irányítástartó izometria (legjobb tudásom szerint)
|
| Előzmény: [1540] Fálesz Mihály, 2012-03-18 13:13:44 |
|
| [1540] Fálesz Mihály | 2012-03-18 13:13:44 |
 Nem egyértelmű, hogy mi a kérdés. Mit nevezel "átdarabolás relációnak"? Mi a "tér"? Hány darabra vághatunk? Csak véges sokra, vagy megszámlálható sokra? Csak síklapokkal vághatunk, vagy diszjunkt részhalmazokra bontunk?
Végtelen sok diszjunkt darab megengedése esetén elismételheted a Cantor-Bernstein-Schröder tétel valamelyik bizonyítását.
|
| Előzmény: [1536] Danesz, 2012-03-17 18:42:39 |
|
| [1539] Fálesz Mihály | 2012-03-18 13:05:06 |
 Az egy egyenesen levő szakaszok arányai között több összefüggést találhatsz akár közvetlenül, akár a Menelaosz-tétel felírásával.
Az ADC, BEC, APE, BPD egyeneseken a különböző szakaszok arányát kifejezheted a területekkel, például 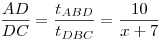 . .
Ezekből összerakhatod a megoldást...
|
| Előzmény: [1537] Sudárné, 2012-03-18 09:32:48 |
|
|
| [1537] Sudárné | 2012-03-18 09:32:48 |
 A feladat a következő: Egy háromszög egy-egy oldalán vegyünk fel egy-egy tetszőleges pontot (jelöljük mondjuk D-vel és E-vel) Ezeket a pontokat kössük össze a velük szemközt lévő háromszög csúcsával. A háromszög így négy részre bomlott, három háromszögre és egy négyszögre, A három háromszög területét ismerem, kérdés a négyszög területe.
Az ábrán találhatóak a további adatok.
|
 |
|
| [1536] Danesz | 2012-03-17 18:42:39 |
 Üdv mindenkinek! Segítenétek egy feladat kidolgozásában? Bizonyítandó, hogy a tér részhalmazain értelmezett átdarabolás relációra igaz, hogy ha A átdarabolható B egy részhalmazába, és B átdarabolható A egy részhalmazába, akkor A átdarabolható B-be. (A átdarabolható B-be, ha létezik az A=U(A(i)) véges diszjunkt felbontás és B=U(B(i)) véges diszjunkt felbontás, hogy A(i) mozgással átvihető B(i)-be)
[U az unió jele]
|
|
|
|
| [1533] BohnerGéza | 2012-01-11 00:58:59 |
 Mint HoA megoldásából is látszik, ha P közelebb van a vezéregyeneshez mint a fókuszpont, de P nincs a tengelyen, akkor is igaz az 1531-beli állítás. Ekkor a nagyítás aránya negatív.
|
| Előzmény: [1532] HoA, 2012-01-08 16:41:15 |
|
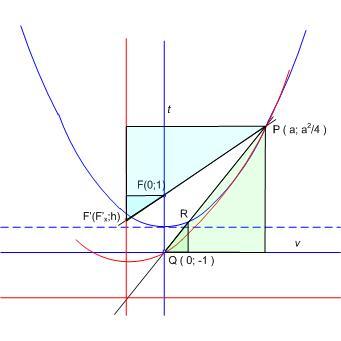
| [1532] HoA | 2012-01-08 16:41:15 |
 Nem nagy a tolongás. Egy mechanikus bizonyítás, mely talán kedvet vagy ötletet ad egy szemléletesebbhez: Válasszuk úgy a koordinátarendszer egységét, hogy a parabola egyenlete 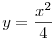 legyen. Ekkor F koordinátái ( 0;1) , v és t metszéspontja Q( 0;-1) . Legyen legyen. Ekkor F koordinátái ( 0;1) , v és t metszéspontja Q( 0;-1) . Legyen 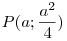 , ahol a feltétel szerint a>2 . A PQ egyenes és a parabola második metszéspontjára ( R ) felírt, x-re adódó másodfokú egyenletből (x-a) kiemelhető, a másik megoldás , ahol a feltétel szerint a>2 . A PQ egyenes és a parabola második metszéspontjára ( R ) felírt, x-re adódó másodfokú egyenletből (x-a) kiemelhető, a másik megoldás 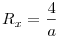 . A nagyítás során R képe Q, F képe F' ,ennek ordinátája legyen h. A lineáris méretek azonos nyújtása miatt a zöld illetve kék hasonló háromszögek hasonlósági aránya megegyezik: . A nagyítás során R képe Q, F képe F' ,ennek ordinátája legyen h. A lineáris méretek azonos nyújtása miatt a zöld illetve kék hasonló háromszögek hasonlósági aránya megegyezik: 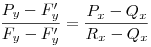 ; ; 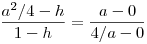 ; ; 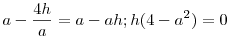 , ebből pedig a > 2 miatt h=0 . , ebből pedig a > 2 miatt h=0 .
|
 |
| Előzmény: [1531] BohnerGéza, 2011-12-31 01:11:20 |
|
| [1531] BohnerGéza | 2011-12-31 01:11:20 |
 jonas [1530]: Azért ne ijesszük el az olvasókat. Megy egyszerűbben is! HoA leírásából nem következik?
(Úgy látom, leszoktunk a feladatok sorszámozása.) Egy másik feladat:
|
 |
|
|
|









 =60o és a=fb. Ilyenkor a feladat a 40/60/80 fokos szögű háromszög megszerkesztését kéri.
=60o és a=fb. Ilyenkor a feladat a 40/60/80 fokos szögű háromszög megszerkesztését kéri. 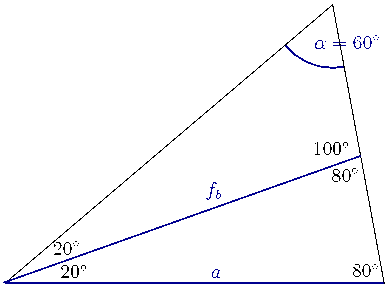



 értékére.
értékére.
 2-re
2-re


