|
| [1574] Fálesz Mihály | 2012-07-14 15:57:42 |
 182. feladat (az idei olimpia 5. feladata, javasolta: Josef Tkadlec, Csehország).
Legyen az ABC háromszögben BCA =90o, és legyen D a C-ből induló magasságvonal talppontja. Legyen X a CD szakasz belső pontja. Legyen K az AX szakasznak az a pontja, amire BK=BC. Hasonlóan, legyen L a BX szakasznak az a pontja, amire AL=AC. Legyen M az AL és BK egyenesek metszéspontja. =90o, és legyen D a C-ből induló magasságvonal talppontja. Legyen X a CD szakasz belső pontja. Legyen K az AX szakasznak az a pontja, amire BK=BC. Hasonlóan, legyen L a BX szakasznak az a pontja, amire AL=AC. Legyen M az AL és BK egyenesek metszéspontja.
Bizonyítsuk be, hogy MK=ML.
Szerintem ez volt az olimpia legviccesebb feladata.
|
|
|
| [1572] sakkmath | 2012-07-03 23:49:10 |
 A Grinberg-cikk 4. oldalának 4. ábrája alapján írjuk fel az általánosított Ptolemaiosz-tételt az egységsugarú kör köré írt ABCD érintőnégyszögre.
Ekkor a cikk 24. oldalának 14. tételében speciálisan  =1. Ezzel előáll az A.536. feladat kiindulási feltétele, s így e feladat érdekes geometriai megközelítését kapjuk. Erre utaltam a Lejárt határidejű KÖMAL feladatokról/[685]-ös hsz-ben. Az akkor említett "elakadáson" hamar túljutottam :-) =1. Ezzel előáll az A.536. feladat kiindulási feltétele, s így e feladat érdekes geometriai megközelítését kapjuk. Erre utaltam a Lejárt határidejű KÖMAL feladatokról/[685]-ös hsz-ben. Az akkor említett "elakadáson" hamar túljutottam :-)
|
| Előzmény: [1566] sakkmath, 2012-05-25 22:06:36 |
|
| [1571] HoA | 2012-05-27 20:42:54 |
 Az egyik irány elemi geometriai bizonyítása triviális. Mivel az átlók által bezárt szomszédos szögek összege 180o, a félszögek összege 90o, tehát ha az egyenesek felezik az átlók szögeit, akkor merőlegesek egymásra.
|
| Előzmény: [1570] Vonka Vilmos Úr, 2012-05-27 20:25:16 |
|
| [1570] Vonka Vilmos Úr | 2012-05-27 20:25:16 |
 A 181. feladat állításának belátásához elegendő azt ellenőrizni, hogy a szóban forgó négy egyenes harmonikus sugárnégyest alkot. Mivel ugyanis tetszőleges szöget tekintve a belső és külső szögfelezők harmonikusan választják el a szögszárakat (és a belső és a külső szögfelező pedig merőleges egymásra), az állítás mindkét oldala innen a harmonikus elválasztás tulajdonságait alkalmazva egyszerűen végiggondolható.
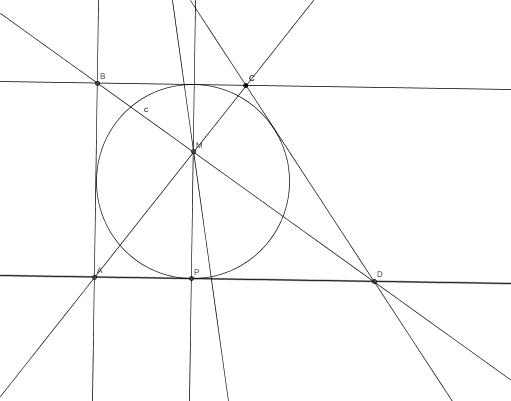
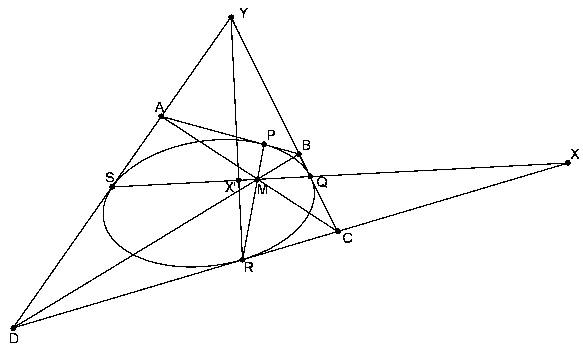
Azt, hogy a négy egyenes harmonikus sugárnégyest alkot, projektív geometriai módszerrel kicsit általánosabban, tetszőleges kúpszelet köré írt négyszögre fogom belátni. Az ábra jelöléseit használva, azt kell ellenőrizni, hogy (MC,MD,MR,MX) harmonikus sugárnégyes. Ez pontosan akkor teljesül, ha (CDRX) harmonikus pontnégyes, ami pedig a Pappos-Steiner tétel miatt ekvivalens azzal, hogy (QSX'X) harmonikus pontnégyes. Ez pontosan akkor teljesül, ha X és X' konjugáltak a négyszögbe írt kúpszeletre nézve. Mivel azonban látható, hogy Y polárisa QS, Y és X konjugáltak. Így X polárisa az RY=RX' egyenes, amiből következik, hogy X és X' valóban konjugáltak.
Természetesen érdekes lehet az eredeti állításra egy elemi geometriai bizonyítás is.
|
 |
| Előzmény: [1569] m2mm, 2012-05-27 18:19:14 |
|
| [1569] m2mm | 2012-05-27 18:19:14 |
 181. feladat: Bizonyítsuk be, hogy egy érintőnégyszög beírt körének szemközti érintési pontjait összekötő e1,e2 egyenesek pontosan akkor felezik az átlók által bezárt szöget, ha e1 és e2 merőlegesek egymásra.
|
| Előzmény: [1561] HoA, 2012-05-25 14:43:58 |
|
|
|
|
| [1565] m2mm | 2012-05-25 21:11:30 |
 "Egy érintőnégyszög beírt körének szemközti érintési pontjait összekötő egyenes áthalad az átlók metszéspontján."
Ez igaz. Legyen ABCD érintőnégyszög, AB és CD egyenesek metszéspontja a projektív síkon E, AD és BC-é F.
Gondold meg, hogy létezik vetítések egy szorzata(síkokra vetítünk), hogy a beírt kör körbe menjen, EF egyenes pedig ideálisba. Illeszkedéstartóság miatt az érintőnégyszög oldalegyeneseinek a képei érintik a kapott kört: ABCD A'B'C'D' képe érintőnégyszög. Mivel EF ideálisba ment, így A'B'||C'D' és A'D'||B'C', tehát A'B'C'D' paralelogramma és érintőnégyszög: rombusz. A rombusz szimmetriaközéppontján pedig nyilván átmegy az összes kérdéses egyenes. Az illeszkedés tartása miatt így az eredeti érintőnégyszögben is egy ponton mentek át a kérdéses egyenesek.
|
| Előzmény: [1561] HoA, 2012-05-25 14:43:58 |
|
|
|
|
| [1561] HoA | 2012-05-25 14:43:58 |
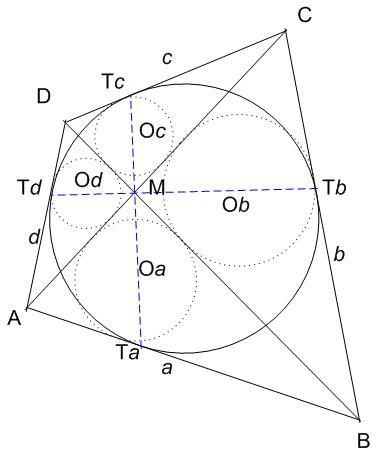
 [1553] ábráját nézve bennem az merült fel: igaz-e, hogy pl. M, Oc és az érintőnégyszög beírt körének [1553] ábráján csak fekete pöttyel jelölt érintési pontja c-n (Tc) egy egyenesen van? Lehet, hogy ez közismert, de Vonka Vilmos úr hivatkozásaiban - és az onnan elérhető hivatkozásokban - nem láttam megemlítve. Vagy kicsit másképp fogalmazva, igaz-e a sejtés:
Egy érintőnégyszög beírt körének szemközti érintési pontjait összekötő egyenes áthalad az átlók metszéspontján és felezi az átlók által bezárt szöget.
|
 |
| Előzmény: [1553] BohnerGéza, 2012-05-22 09:26:24 |
|
| [1560] m2mm | 2012-05-23 15:23:10 |
 A feladat egy megoldása már fenn van a fórumon, a Lejárt határidejű KöMaL feladatokról [693] hozzászólásában. Ha jól látom a szintetikustól nem sokkal tér el (ő Desarguesozik én meg harmonikus pontnégyeseket használok az egyik lépésben).
|
| Előzmény: [1558] Vonka Vilmos Úr, 2012-05-23 07:00:15 |
|
| [1559] HoA | 2012-05-23 09:19:03 |
 A 179. feladat megoldása: Válasszuk úgy a betűzést, hogy Oc és Ob különböző távolságra legyen az AC átlótól, mint az ábrán is. ( Ha nincs ilyen lehetőség, akkor a négy kis háromszögbe írt kör sugara egyenlő és könnyen belátható, hogy érintőnégyszögünk rombusz, amelyre már szimmetria okokból is könnyen adódik A. 549 állítása ).
Érintőnégyszögünket az AC átlóra tükrözve és a betűzést az eredeti körüljárás szerint elvégezve az ObOcOd körre vonatkozó állítás most tkp. az eredeti ábra ObOcOa körére vonatkozik, tehát ha az első igaz, akkor a második is és viszont.
Az ObOcOd kör Ob és Oc –beli érintőinek metszéspontja legyen C1. Mivel ez rajta van MC-n és egyenlő távolságra van Ob-től és Oc-től, így MC és ObOc f felező merőlegesének metszéspontja. Ebből ObOcOd kör O1 középpontja is egyértelmű: mivel Ob és Oc rajta van az O1C1 átmérő Thálesz-körén, O1 az ObOcC1 kör és f másik metszéspontja.
A fentiekben Od-t nem használtuk fel, így ugyanerre az eredményre jutunk, ha az ObOcOa körből indulunk ki. A két kör középpontja tehát azonos és van a körvonalaknak közös pontja, pl. Ob, tehát a két kör egybeeseik, OaObOcOd egy körön vannak.
|
| Előzmény: [1553] BohnerGéza, 2012-05-22 09:26:24 |
|
| [1558] Vonka Vilmos Úr | 2012-05-23 07:00:15 |
 Egyébként az eredeti A. 549-es feladat "előéletével" és általánosításaival kapcsolatban itt van egy érdekes cikk, elsősorban a 4. fejezetet és a kapcsolódó hivatkozásokat érdemes megnézni. Ebben a folyóiratban a 243. oldalon az állítás a megfordításával együtt be van látva, de itt szintetikus bizonyítás is olvasható.
|
| Előzmény: [1557] BohnerGéza, 2012-05-23 03:50:33 |
|
|
|
|
| [1554] Lóczi Lajos | 2012-05-22 12:45:05 |
 180. feladat. Valamely p és q valós számok esetén tekintsük az f(x):=x2+px+q polinomot.
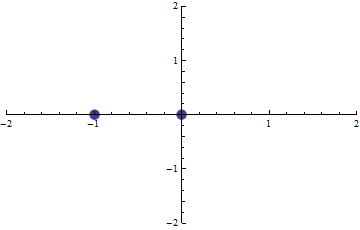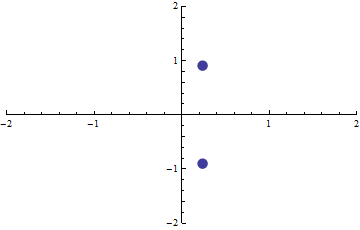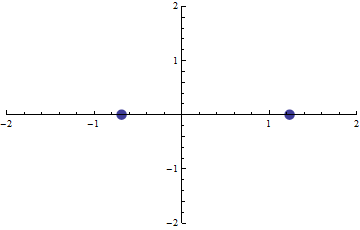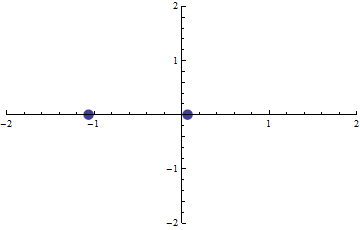
A (p,q) pont a síkon fussa be az origó középpontú egységsugarú körvonal peremét. Ekkor az f(x)=0 egyenlet gyökei a (komplex) síkon szintén körbejárnak.
Milyen alakzat áll elő így a gyökök mozgása során? Mutassuk meg, hogy
-- a (komplex) síkon az alakzatot magába foglaló, origó középpontú és minimális sugarú kör sugara 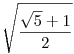 , ,
-- az alakzat területe pl. 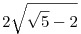 és és 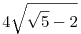 közé esik. közé esik.
|
|
| [1553] BohnerGéza | 2012-05-22 09:26:24 |
 Az alábbi feladat megoldása nem jelent meg a KÖMAL-ban.
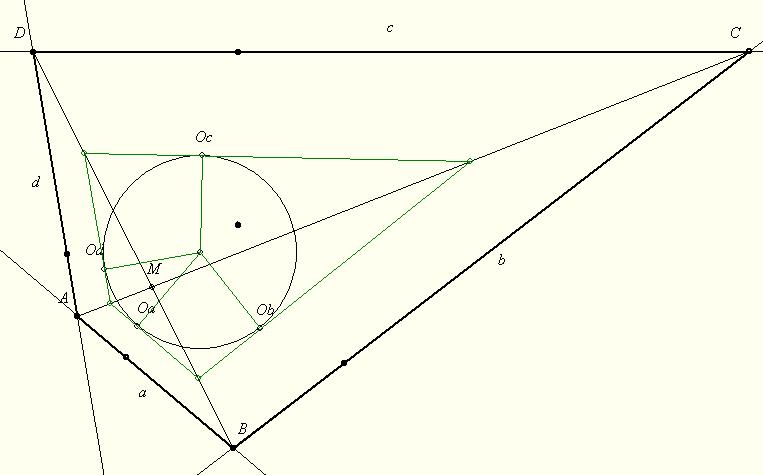
A. 549. Az ABCD érintőnégyszög átlói az M pontban metszik egymást. Mutassuk meg, hogy az ABM, BCM, CDM és DAM háromszögekbe írt körök középpontjai egy körön vannak.
A feladattal kapcsolatban a következő merült föl:
Legyenek a megfelelő középpontok Oa, Ob, Oc és Od. Az új állítás: Az ObOcOd körhöz az Ob-ben és Oc-ben húzott érintők az MC egyenesen metszik egymást. (Ennek bizonyítása valószínűleg az eredeti A. 549. feladattal egyforma nehézségű, vagy nehezebb.)
Viszont annak bizonyítása, hogy ebből az új állításból következik az eredeti, már emberi léptékű.
179. feladat: Bizonyítandó, hogy az új állításból következik az A. 549. feladat állítása.
|
 |
|
| [1552] BohnerGéza | 2012-05-09 11:13:00 |
 Maradok a nálam szokásos jelöléseknél, így kevesebb elírás várható.
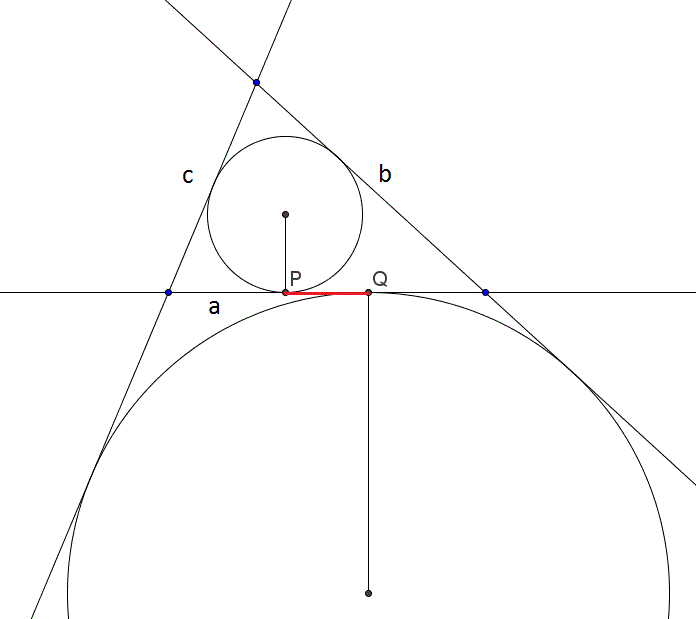
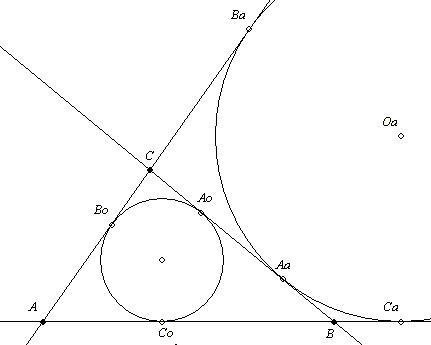
Az oldalakon az érintési pontokat a szemközti csúcs nagybetűjével és indexekkel jelölöm: a beírt körhöz a 0, az érintőkörökhöz belül érintett oldal (a, b, c) az index.
Külső pontból a körhöz húzott két érintőszakasz hossza megegyezik:
ABo = ACo = x, BCo = BAo = y, CAo = CBo = z.
2(x+y+z)= k (kerület) x+y+z = s (félkerület), ahonnan pl.
x = s-(y+z) = s-a
Magyarul: Csúcstól a beírt körig tartó érintőszakaszt kapjuk, ha a félkerületből levonjuk a szemközti oldalt.
Mivel BCa = BAa, CAa = CBa és ABa = ACa, 2s = AaC+CA+AB+BCa = BaA+ACa.
Tehát ABa = ACa = s. Magyarul: Csúcstól a szemközti hozzáírt körig tartó érintőszakasz hossza a félkerület.
Ezeket tudva beláthatod, hogy kérdésedre a válasz PQ = |b-c|.
Érdekes eredményeket kapsz, ha meghatározod például a következő szakaszok hosszát:
CoCa, CbCa, BCa, BCo, ... (egy oldalegyenesen van két csúcs és 4 érintési pont, bármely kettő távolsága meghatározható.)
Ezek ismerete szerkesztési feladatokban is segíthetnek.
|
 |
| Előzmény: [1550] matekpelducik, 2012-05-08 22:26:30 |
|
|




 =90o, és legyen D a C-ből induló magasságvonal talppontja. Legyen X a CD szakasz belső pontja. Legyen K az AX szakasznak az a pontja, amire BK=BC. Hasonlóan, legyen L a BX szakasznak az a pontja, amire AL=AC. Legyen M az AL és BK egyenesek metszéspontja.
=90o, és legyen D a C-ből induló magasságvonal talppontja. Legyen X a CD szakasz belső pontja. Legyen K az AX szakasznak az a pontja, amire BK=BC. Hasonlóan, legyen L a BX szakasznak az a pontja, amire AL=AC. Legyen M az AL és BK egyenesek metszéspontja. 

 =1. Ezzel előáll az A.536. feladat kiindulási feltétele, s így e feladat érdekes geometriai megközelítését kapjuk. Erre utaltam a Lejárt határidejű KÖMAL feladatokról/[685]-ös hsz-ben. Az akkor említett "elakadáson" hamar túljutottam :-)
=1. Ezzel előáll az A.536. feladat kiindulási feltétele, s így e feladat érdekes geometriai megközelítését kapjuk. Erre utaltam a Lejárt határidejű KÖMAL feladatokról/[685]-ös hsz-ben. Az akkor említett "elakadáson" hamar túljutottam :-)