| [1776] Sinobi | 2013-12-11 18:15:18 |
 Adott a síkon négy pont. Tekintsük az összes kúpszeletet, amelyek áthaladnak ezen a négy ponton. Mi az ilyen tulajdonságú kúpszeletek középpontjának mértani helye?
Adott a síkon négy egyenes. Tekintsük az összes kúpszeletet, amelyek érintik ezt a négy egyenest. Mi az ilyen tulajdonságú kúpszeletek középpontjának mértani helye?
|
| Előzmény: [1749] Sinobi, 2013-10-30 20:58:07 |
|
| [1775] Sinobi | 2013-11-28 21:28:47 |
 Mivel A'B'C< + CB'C'< = 60 fok, ezért A'B'C'< kisebb kell legyen 60 foknál... Én is ezzel a remek ellenbizonyítással kaptam a feladatot.
Annyit tennék még hozzá, hogy a szemlélet szerint A'B', B'C', C'D' és D'A' szakaszok ugyanakkorák, de a szemlélet nem indokolja hogy A'C' és B'D' is ugyanakkora legyen velük, szögekről meg pláne nem mond semmit.
Na de mekkorák a szögei?
|
| Előzmény: [1774] HoA, 2013-11-28 13:29:02 |
|
|
| [1773] Sinobi | 2013-11-28 08:04:56 |
 ABCD egy egységnyi oldlélű szabályos tetraéder. Legyen A' az A pont B-re vonatkozó tükörképe, B' a B pont C-re vonatkozó tükörképe, s.í.t. ciklikusan!
Határozzuk meg az így kapott A'B'C'D' tetraéder élszögeit.
|
|
|
| [1771] w | 2013-11-24 11:59:46 |
 B.4562-re egy érdekes megközelítés:
Tekintsük azt az E középpontú 90 fokos  forgatva nyújtást, amire forgatva nyújtást, amire  (A)=C. Legyen az (A)=C. Legyen az 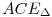 képe a képe a 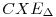 ! Ekkor X olyan pont, melyre AC és CX merőleges egymásra (hisz a forgatás szöge 90 fokos), továbbá AEX ! Ekkor X olyan pont, melyre AC és CX merőleges egymásra (hisz a forgatás szöge 90 fokos), továbbá AEX =AEC =AEC +90o=180o. Vagyis X rajta van a BC és AE egyenesen is, emiatt X=B és így +90o=180o. Vagyis X rajta van a BC és AE egyenesen is, emiatt X=B és így  (C)=B. Tehát az AC egyenes képe a BC egyenes, amiért F képe, Y, a BC egyenesen van. Mivel viszont a BC egyenes D és Y pontjára is igaz, hogy FED (C)=B. Tehát az AC egyenes képe a BC egyenes, amiért F képe, Y, a BC egyenesen van. Mivel viszont a BC egyenes D és Y pontjára is igaz, hogy FED =90o=FEY =90o=FEY , ezért D=Y kell legyen. Ha pedig F az ACE kör középpontja, akkor D középpontja lesz a , ezért D=Y kell legyen. Ha pedig F az ACE kör középpontja, akkor D középpontja lesz a  (ACE)=CBE körnek. Tehát (ACE)=CBE körnek. Tehát  egyenlő szárú lesz. egyenlő szárú lesz.
|
|
| [1770] w | 2013-11-24 00:00:56 |
 1. A megoldás 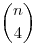 , mert az AC és BD átló pontosan akkor metszi egymást, ha ABCD négyszög konvex (lehetne konkáv és hurkolt is), és annyi konvex négyszög van, amennyiféle csúcsnégyes választható ki. , mert az AC és BD átló pontosan akkor metszi egymást, ha ABCD négyszög konvex (lehetne konkáv és hurkolt is), és annyi konvex négyszög van, amennyiféle csúcsnégyes választható ki.
2. A mértani hely egy szakasz, két parabolaív és egy negyedkörív. Ennek belátása egészen triviális, rád hagyom.
|
| Előzmény: [1767] Kardos, 2013-11-21 18:24:23 |
|
|
| [1768] Sinobi | 2013-11-23 12:39:35 |
 Definiáld a térbeli inverzió esetén a szögtartóságot, és bizonyítsd be!
|
|
|
| [1766] w | 2013-11-21 18:08:36 |
 Az 1. feladatra segítség: vegyél tetszőleges két átlót: AC-t és BD-t, majd nézd meg az ABCD négyszöget. ;-)
A 2. feladatban a két félegyenes legyen az x-tengely és az y-tengely nemnegatív része. A mértani helyet egyenként keresd meg a négy síknegyedben.
|
| Előzmény: [1765] Kardos, 2013-11-21 17:10:08 |
|
| [1765] Kardos | 2013-11-21 17:10:08 |
 Hali mindenkinek! Valaki tudna ezekben segíteni!?
1) Adott egy konvex n szög. Hány olyan átlópárja van, amelyek a sokszög belsejében metszik egymást.
2) Adott két közös kezdőpontú egymásra merőleges két félegyenes. Mi azon pontok mértani helye a síkban, amelyeknek a két félegyenestől mért távolságának összege állandó?
|
|
|
| [1763] Sinobi | 2013-11-19 19:03:04 |
 Ez nagyon tetszik! Bár nem sokban különbözik a másik megoldástól, mégis, talán valamivel erősebb eszközt használ.
,,van olyan térbeli inverzió, ami a k0 és u köröket párhuzamos (síkú) körökbe viszi."
Ezt talán érdemes belátni. Kérdés2: és mi igaz, ha a körök egymáson kívülre esnek? Mindegy.
Nagyrészt erre a módszerre építve álljon itt egy bizonyítás(?) az általánosított kis-Monge lemmára:
Ha adott k1, k2 körök (egymáson kívül) és egy k3 kör, amely ugyanakkora szögben metszi k1-t és k2-t, akkor az S1 S2 S3 S4 metszéspontokat összekötő egyenesek a k1 k2 körök (külső) has. pontjában (H-ban) fogják egymást metszeni.
Felveszem k4 és k5 köröket, hogy mindketten (belülről) érintsék k1 k2 köröket, és tartalmazzák k3-t. Azt fogom belátni, hogy S1 S4 x S2 S3 egyenesek S metszéspontja k3 k4 körök hatványvonalán fekszik. Ugyanígy k3 k5 körök hatványvonalán is, tehát k4 k5 körök hatványvonalán is, de k4 k5 körök hatványvonala k5 kör változtatásával változik, az egyetlen fixpontjai k1 k2 H has pontja (ez k1 k2-t érintő körökre már beláttatott) és S, amelyek következésképpen egybeesnek. (talán érdemes lett volna felvenni egy k6 kört...)
Alkalmazok egy térbeli inverziót, hogy k3 és k4 egy síkba kerüljenek, ekkor k1 és k2 ugyanakkora szögben metszik k3-t, és k4-t érintik, tehát ugyanakkorák, tehát S1 S2 S3 S4 egy húrtrapéz. Tehát S1S4 phuzamos S2S3 egyenessel. Az is igaz, hogy egy ilyen inverziónál k3 k4 hatványvonalából lesz a végtelen távoli egyenes (ezt is érdemes meggondolni), tehát S rajta van k3 k4 hatványvonalán.
Persze ez így hosszú, és bonyolult, és még hosszabb, ha kifejtem azokat, amikre épít. Most nem jut hirtelen más az eszembe, ahol alkalmazhatok egy részint szögtartó, részint ideális egyenessel operáló transzformációt, de ötleteket szívesen fogadok.
|
|
| [1762] Fálesz Mihály | 2013-11-19 11:26:22 |
 1. S1S2S3S4 húrnégyszög. Körülírt köre legyen u, középpontja U.
2. A k0 és u közöknek nincs közös pontja (pl. mert a k1,k2,k3,k4 körök lefedik u-t). Ebből következik, hogy van olyan térbeli inverzió, ami a k0 és u köröket párhuzamos (síkú) körökbe viszi. Vegyünk egy ilyen inverziót, a pólusa legyen X. A sík képe gömbfelület, körök és egyenesek képe a gömbre illeszkedő kör; egymást érintő görbék képei egymást érintő görbék. A k1' és k3' kör, illetve a k2' és k4' kör ugyanakkora, S1'S2'S3'S4' téglalap, T1'T2'T3'T4' négyzet.
3. Legyen S*=S1'S3' S3'S4' és T*=T1'T3' S3'S4' és T*=T1'T3' T3'T4' az u', iletve a k0' kör középpontja. X,S,S* kollneáris és X,T,T* is kollneáris. A k0',k0,u',u körök szimmetrikusak az XS*T* síkra, ezért O és U az XS*T* síkban van. S,T,O,U közös pontja az eredeti síknak és az XS*T* síknak, tehát egy egyenesen vannak. T3'T4' az u', iletve a k0' kör középpontja. X,S,S* kollneáris és X,T,T* is kollneáris. A k0',k0,u',u körök szimmetrikusak az XS*T* síkra, ezért O és U az XS*T* síkban van. S,T,O,U közös pontja az eredeti síknak és az XS*T* síknak, tehát egy egyenesen vannak.
|
| Előzmény: [1761] HoA, 2013-11-19 10:36:57 |
|
|
|
|
| [1758] w | 2013-11-15 17:49:01 |
 Ez a megközelítés is nagyon tetszik, ezt nem vettem észre. (Amit írtam bizonyítás abból a tévhitből jött, hogy S1S2S3S4 az O1O2O3O4 négyszög beírt köre, aztán sikerült kipontosítani. :-)
|
| Előzmény: [1756] HoA, 2013-11-15 14:36:35 |
|
|
|
| [1754] Sinobi | 2013-11-13 18:13:22 |
 Ehhez kapcsolódik egy inverzós Monge-tétel bizonyítás.
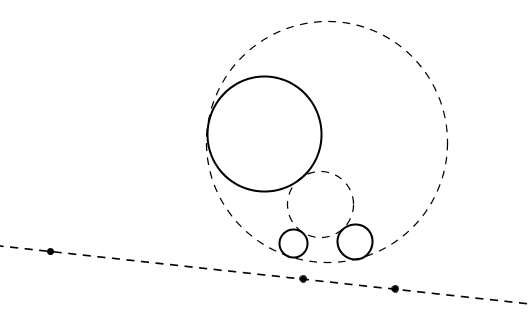
Először belátjuk inverzióval a kis Monge-tételt három érintkező körről: k2 T1-ben és T3-ban érinti k1 és k3 köröket. Legyen Z a T1T3 egyenes és a k1 k3 centrálisának metszése. Innen egy olyan inverzió, amely kicseréli a T1 és T3 pontokat, helybenhagyja a k2 kört, mert kicseréli egy pontpárját. A k1 és k3 körök képeinek középponjtai a centrálison maradnak, és rajta maradnak az O2 T1 és az O2 T3 egyeneseken, tehát kicserélődnek. Három érintkező kör esetén T1 T3 átmegy k1 és k3 (egyik) egymásba invertálási pontján, és a k1-k3-at kicserélő inverzió helyben hagyja k2-t.
Három általános helyzetű körre pedig a bizonyítás: felveszek még két kört (k4-et és k5-öt), amely mind a három kört érinti, és akkor a k1-k2, k2-k3, k1-k3 körök (egyik) egymásba invertálási pontjai rajta fekszenek k4 és k5 hatványvonalán. Persze ez bizonyítás szinten sokkal-sokkal több szőrözést igényel, de legalább inverzió, körhatvány és efféle, és nem tér és projektív.
|
 |
| Előzmény: [1753] w, 2013-11-13 16:43:01 |
|
| [1753] w | 2013-11-13 16:43:01 |
 Egy lehetséges megoldás az A.597-re.
1. Felhasználjuk Monge tételét. Ez alapján kapjuk, hogy S1S2 S3S4 S3S4 T1T3=H13 és S2S3 T1T3=H13 és S2S3 S4S1 S4S1 T2T4=H24. T2T4=H24.
2. Rendkívül lényeges a következő lemma. Adott négy kör a síkon:  1, 1,  2, 2,  3, 3,  4, ahol 4, ahol  i és i és  i+1 az Ei pontban kívülről érinti egymást. Ekkor ha i+1 az Ei pontban kívülről érinti egymást. Ekkor ha  i középpontja Li, akkor L1L2L3L4 nyilván érintőnégyszög, de ekkor az LiLi+1Li+2 i középpontja Li, akkor L1L2L3L4 nyilván érintőnégyszög, de ekkor az LiLi+1Li+2 -ek szögfelezői egy pontban metszik egymást, ahonnan E1E2E3E4 húrnégyszög. -ek szögfelezői egy pontban metszik egymást, ahonnan E1E2E3E4 húrnégyszög.
3. Belátjuk, hogy az s:=S1S2S3S4 és a k0 körök hatványvonala H13H24. Valóban, például H13 hatványa k0-ra nézve H13T1.H13T3, s-re nézve pedig H13S1.H13S2. Ezek megegyeznek az előbbi lemma és a szelőtétel miatt. Hasonlóan, H24 is a hatványvonalon van, kész.
Legyen s középpontja 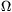 . Beláttuk, hogy O . Beláttuk, hogy O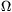 merőleges h:=H13H24 egyenesre. merőleges h:=H13H24 egyenesre.
4. Mivel azt már megmutattuk, hogy H13S3.H13S4=H13S1.H13S2=H13T1.H13T3, ezért k2, k4 és k0 körök hatványpontja H13. Hasonlóan, a k1, k3 és k0 körök hatványpontja H24. Vagyis H13 polárisa k0-ra nézve T2T4 és H24 polárisa T1T3. Innen OT is merőleges h-ra, tehát T O O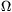 . .
5. A polaritás ismert tulajdonságai miatt H13H24 pólusa s-re nézve S. Következményül 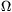 S is merőleges h-ra, azaz S S is merőleges h-ra, azaz S O O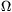 . .
Ezért O, T és S is rajta van O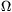 egyenesen. egyenesen.
|
|
|
|






 forgatva nyújtást, amire
forgatva nyújtást, amire  =AEC
=AEC
 S3'S4' és T*=T1'T3'
S3'S4' és T*=T1'T3'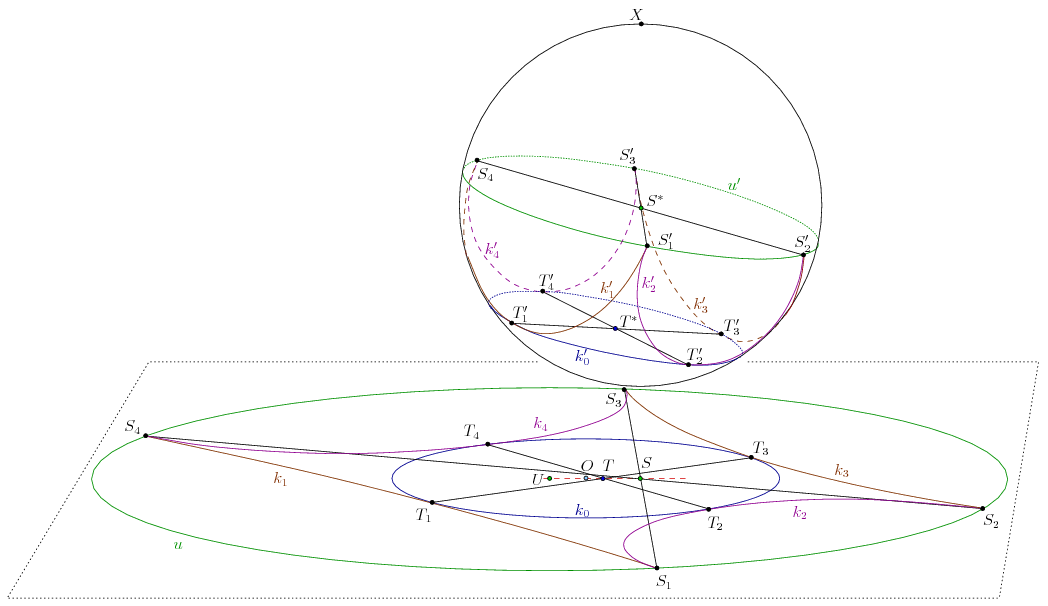

 .
. >1 , S1S2 másik metszéspontja k3 -mal P , S3S4 -é Q . A hasonlóság miatt H13S4=
>1 , S1S2 másik metszéspontja k3 -mal P , S3S4 -é Q . A hasonlóság miatt H13S4=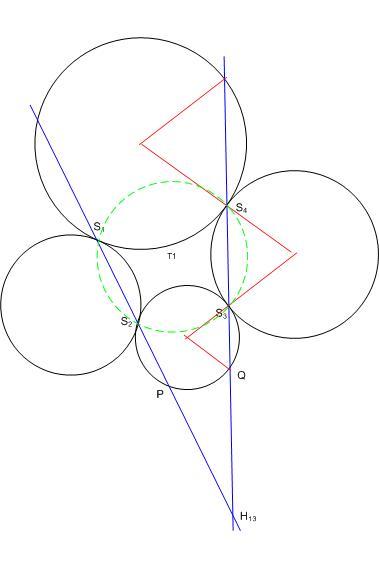

 1,
1,  . Beláttuk, hogy O
. Beláttuk, hogy O O
O