Fórum: GEOMETRIA

Nézeetek meg a forrását: http://www.artofproblemsolving.com/Forum/viewtopic.php... International Zhautykov Olympiad 2014 D2 P6 www.artofproblemsolving.com Four segments divide a convex quadrilateral into nine quadrilaterals. The points...

Talán a leggyorsabb megoldási lehetőség azt használja ki, hogy ABCD akkor és csak akkor érintőnégyszög, ha

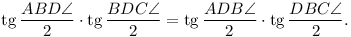
Ennek ellenére úgy emlékszem, hogy számítások nélküli megoldás is van, de azt direkt nem olvastam el. (Monge-tétel?...)

Ezt nem tudom. Leloned, kerlek?

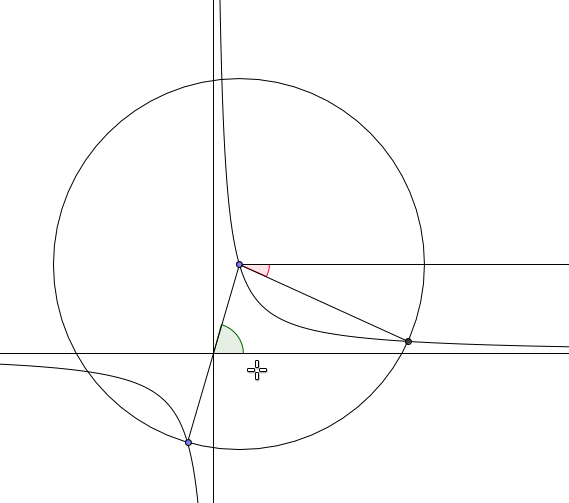
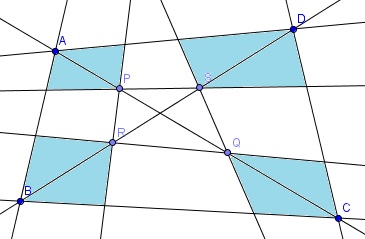
Adott az ABCD négyszög, valamint az AC átlón a P és Q; a BD átlón az R és S pontok. A PR, QS, PS, QR egyenesek kilenc négyszögre osztják ABCD-t "3x3-as táblázat alakban".

Tegyük fel, hogy a csúcsokhoz legközelebbi négy kis négyszög érintőnégyszög. Igazoljuk, hogy a középső is az!

Nekem a kérdés szerkesztéselméletinek tűnik. Ha adottak a kúpszelet paraméterei, akkor elvileg megszerkeszthetők azok az együtthatók, melyekre Ax²+Bxy+Cy²+Dx+Ey+F=0 a kúpszelet egyenlete. Feltehetően elmetszettük az x²+y²=1 körrel; behelyettesítéssel és négyzetreemeléssel adódik, hogy a metszéspontok x és y koordinátái egy-egy szerkeszthető együtthatójú, legfeljebb negyedfokú egyenlet gyökei. Ha csak egy metszéspont adott, nem csoda, hogy bizonyos esetben szerkeszthetetlen a többi, hisz ahhoz egy harmadfokú egyenlet gyökeit kellene megszerkeszteni, ami mint tudjuk, nem mindig tehető meg. Ha két vagy három metszéspont adott, akkor a maradék metszéspont koordinátáira egy legfeljebb másodfokú egyenlet adódik, az pedig megoldható szerkesztéssel. Tehát ha 2 vagy 3 metszéspont adott, mindig meg lehet csinálni, ha 0 vagy 1, akkor pedig nem mindig.

Ket korivnek csak akkor lehet vegtelen sok kozos pontjuk, ha ugyanannak a kornek az ivei. Legyen ez a kor k.

Legyen k sugara r, a kibovitett sinus tetel miatt vagy alfa=beta, vagy alfa=180-beta.

A szelotetel miatt egy szogszar egy k korbol csak akkor metsz ki ket a hosszu szakaszt, ha a szakaszok, es a kor tukrosek a szogszar belso szogfelezojere.

Nem nehez konstrukciot adni, hogy minden alfa=beta<90 -re, es minden alfa=180-beta -ra letezik ilyen szogszar, a hosszu szakaszokkal.

Es alfa=beta>=90 nem jo, mert a belso szogfelezo ket felsikra osztja a sikot, amelyik elvalasztja a latokoriveket, az egyiknek csak az egyik felsikban, a masiknak csak a masik felsikban lesz pontja.

Help, valaki! 14 feladatból ebbe belesültünk: Egy szög két szárán adott 1-1 "a" hosszúságú szakasz. Az egyik szakasz alfa szögű látószögkörívének végtelen sok közös pontja van a másik szakasz béta szögű látószögkörívével. Milyen alfa és béta szög esetén lehetséges ez? és miért?:D

Abbol, hogy 1 db kozos pontjuk van megadva, nem kovetkezik, hogy a tobbi szerkesztheto. Ellenpelda: a Bolyai-féle szögharmadolás.

A 2 db kozos pont esetrol tudsz valami jot?

A Bolyai-féle szögharmadolás:

Ez egy érdekes kérdés, tetszik. Valamiért azt gondoltam elsőre, hogy mindig meg lehet szerkeszteni az összes metszéspontot, de most már nem vagyok biztos benne.

Ha adott egy kupszelet es egy kor es 0/1/2/3 metszespontjuk, akkor mely esetekben szerkesztheto meg a tobbi metszespont, es mely esetekben nem?

köszi - tanulmányozom a magyarazatot!!!

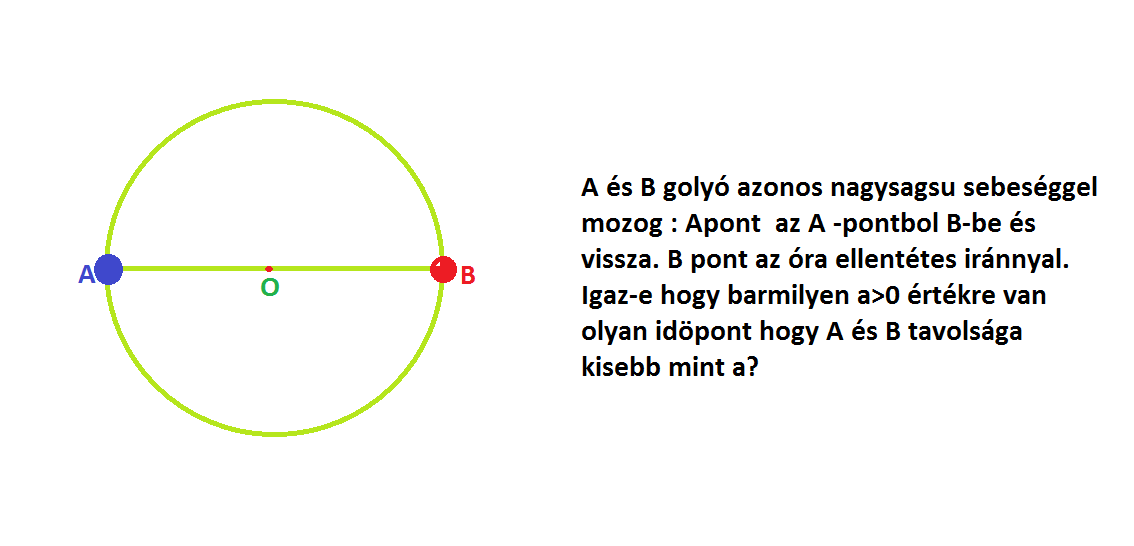
Igen. Még arra sincs szükség, hogy A és B azonos sebességgel mozogjon.

Elég azokat az időpontokat vizsgálni, melyekben az A golyó az eredeti A₀ pontban van. Tegyük fel, hogy ameddig A elmegy B₀-ba és vissza A₀-ba, annyi idő alatt B s^.I utat tesz meg, ahol I a félkörív hossza. Célunk az, hogy belássuk, hogy tetszőleges a>0-hoz van olyan n pozitív egész, melyre ns kisebb, mint a távolságra van egy egész számtól.

Ha s racionális szám, akkor nincs mit bizonyítani, létezik olyan n>0 egész, melyre ns egész szám lesz.

Ha s irracionális, akkor pedig tekintsünk egy hatalmas nagy N-et, és az 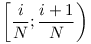intervallumokat i=0,1,...,N-1-re. Mivel s irracionális, ezért {ns} (ns törtrésze) minden n>0-ra más és más értéket vesz fel. Ezért az {ns} számokat minden n=1,2,...,N+1-re véve, ez az N+1 szám benne van előbbi intervallumok egyikében. Skatulya-elv szerint így lesz két n, n₁ és n₂, melyre {n₁s} és {n₂s} ugyanabban az intervallumban van, eltérésük <N^-1. Másfelől mivel triviálisan 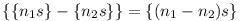, ezért kaptunk egy olyan n=n₁-n₂ számot, melyre {ns}<N^-1, vagyis |n|s egy egész számtól kisebb, mint N^-1 távolságra van. Márpedig N^-1 tetszőlegesen kicsi lehet. (A Kronecker-tételre is hivatkozhattunk volna.)

Összességében tetszőlegesen kis ívhossz lehet A és B távolsága, amiből következik az állítás.

Szép és elemi kérdés, a bizonyítás is nagyon szép, a vélemény szerintem helytálló. A probléma egyébként az IMO 1991/5. feladat.

Persze lehetne vitatkozni, bőven vannak még geometriai szépségek, például ez egészen szép és egyszerű, ám ránézésre egyáltalán nem triviális tétel.

Vietnami matematikusok önkéntes versenyérol( legszebb és legelemibb bizonyitás) idézem egy feladatot :

Az ABC háromszög belsejében van egy P pont. bizonyitando hogy a PAB , PBC, PCA szögek között van 30° -nál nem nagyobb!

kivancsi vagyok a véleményetekre!

Igazad van, nem voltam teljesen alapos, de nem nehéz kipontosítani (látószögek...).

Az állitás hogy ABX vagy ABY közé irható kör sugara nagyobb mint ABC -énél - ezt nem látom!!!

Tekintsük a legnagyobb olyan kört, amely a sokszög valamely három csúcsa köré írható, a három csúcs legyen A,B,C. Belátjuk, hogy ez tartalmazza az egész sokszöget, és három szomszédos csúcson halad át.

Ha ez a kör minden csúcsot tartalmaz, akkor egyben tartalmazza az egész sokszöget. Ezért ha nem tartalmazza az egész sokszöget, akkor van olyan X csúcs, amelyet a kör nem tartalmaz. De ekkor ABX kör nagyobb sugarú lesz az ABC körnél, ami ellentmond választásunknak.

Tegyük fel, hogy nincs olyan három szomszédos csúcs, amelyre a köréjük írt kör sugara maximális. Ekkor az előbb igazoltak szerint van, mondjuk körüljárás szerint A és B között, egy olyan Y csúcs, amely a legnagyobb körön belül található. De ekkor az ABY kör sugara ismét nagyobb lesz, mint ABC sugara, ez ellentmondás.

Egy konvex sokszögnél mindig megtalalható 3 egymast követö csucsot, melyekre a köré irható kör tartalmazza az egész sokszöget?( elemi egyszerü bizonyitas jó lenne)

Köszi a linket Kemény Legény! Igen, az összegnél elírtam, kösz a javítást, de utólag láttam, a sejtésem úgy sem talál Üdv: epsilon

És egy apróság: .

Az alábbi linken van pár bizonyítás a háromszöges esetre: itt.

Ha nem tévedek, a kérdésre a válasz az alábbi lenne, de nem tudom bizonyítani, sem a tetraéderre átültetni :-(

Üdv mindenkinek! A felvetett hasáb számlálási feladat kapcsán előkerült egy másik feladat is: Egy szabályos háromszög minden oldalát osszuk fel n egyenlő részre, majd ezeken át húzzunk az oldalakkal párhuzamos egyeneseket. Így a háromszöget n×n kis kongruens háromszögre osztottuk. Összesen hány háromszög látható az ábrán? Sajnos az eredményre zárt alakban nincs tippem. Olyan megoldás érdekelne, amelyik kiterjeszthető a térbe is, ha a szabályos háromszög helyett szabályos tetraédert tekintünk, és azt bontjuk kis tetraéderekre. Tudna-e valaki segíteni? Előre is köszönöm, üdv: epsilon