| [1851] emm | 2014-07-17 13:09:23 |
 x=a+b épp a magasság oldalfelező merőlgesre vett tükörképe, a koordinátázás meg oldalfüggetlenül szimmetrikus, szóval mind a 3 ilyen egyenesen rajta van, ebből meg kb. adódik a sejtés, hogy így lehetne értelmezni.
|
| Előzmény: [1850] w, 2014-07-17 12:49:11 |
|
|
| [1849] emm | 2014-07-17 12:40:02 |
 Legyen a háromszög ABC, koordinátázunk. A(a,0), B(b,0), C(0,c), P(x,y) legyen egy keresett pont. Ekkor a kerületek rendre
KPAB=(x−a)2+y2+(x−b)2+y2+(b−a)2
KPAC=(x−a)2+y2+x2+(c−y)2+a2+c2
KPBC=(x−b)2+y2+x2+(c−y)2+a2+b2
KPAB−KPAC=−2(b(a−b+x)+c(c−y))=0
KPAC−KPBC=2(b−a)(a+b−x)=0
Innét x=a+b és y=c+2abc. Tudjuk, hogy ebben a koordinátarendszerben a magasságtpont M(0,−abc) és köréírt kör középpontja O(a+b2,ab+c22c), és 2O−M épp az általunk kapott pont, így P a magasságpont középpontra vett tükörképe.
|
| Előzmény: [1848] w, 2014-07-17 11:49:57 |
|
| [1848] w | 2014-07-17 11:49:57 |
 Adott egy ABC háromszög a síkon. Adjuk meg az(oka)t a P pontokat, melyekre az ABP, BCP és CAP háromszögek oldalainak négyzetösszege megegyezik. Keressük meg P geometriai jelentését!
|
|
|
| [1846] Sinobi | 2014-06-24 18:06:01 |
 [1845] az trivialisnak tunik... Bloffre: belatod, hogy X1PX2P' egy erintonegyszog csucsai, felveszed az erintesi pontokat, alkalmazod, hogy egy pontbol egy korhoz huzott ket erinto ugyanolyan hosszu, es azt kapod, |PF1-PF2| = |P'F1-P'F2|, gondolom.
Mas feladat: maximum hany olyan pontpart lehet megadni a sikon, hogy lehessen hozza talalni olyan 2-od rendu gorbesort, hogy minden pontpar mindket eleme ugyanazon a 2-od rendu gorben fekudjon? (ez nem egy krealmany, hanem tenyleg elojott geometria kozben, van, ahol hasznos lenne tudni. En nem tudom)
|
|
| [1845] w | 2014-06-20 23:27:30 |
 Egy ε ellipszisnek és egy H hiperbolának ugyanazok a fókuszai: F1,F2. Mutassuk meg, hogy minden P∈H-ra az Xi=PFi∩ε (i=1,2) jelöléssel F1X2∩F2X1 is H pontja lesz.
|
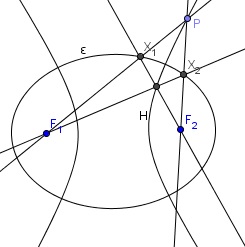 |
|
| [1844] HajduM | 2014-06-20 19:46:03 |
 Üdv!
Fel kell készülnöm mindenre ami szóba jöhet.
Ma volt egy olyan feladatom, amit csőszerelő szakmában izometriának neveznek, ami azt jelenti, hogy meghatározott két pontot össze kell kötni egy csőszakasszal úgy, hogy közben függőleges, vízszintes irányváltásokkal ki kell kerülni gépeket más csöveket stb...
Gyakorlatilag 3 dimenzióban kell gondolkodnunk, és megtervezni, hogy A ponttól B-ig, miként jutunk el egy pl 100 milliméter vastagságú csővel és e szakaszba épített berendezésekkel.
Ha A pont egy kocka bal alsó sarka, B pedig a túl oldali jobb felső, és közben egy 12 fokos, egy 74 fokos, és egy 17 fokos íveltséget kell számolnom, illetve meg kell tudnom, hogy az ívek közötti egyenes szakaszok mekkorák?
Ezt le kell gyártanom a földön, majd esetleg 6 méter magasban, befűzni egy csőhídra, most éppen Kecskeméten az Univer konzervgyár, paradicsomfeldolgozó épülő üzemében.
Tehát alapvetően a megfelelő kérdések megfogalmazásával bajlódom, mert Ti egészen másképpen gondolkodtok, mint ahogyan nekem kell.
Nem elég tudnom a számokat, teljesen el kell tudnom képzelni (vizualizálni) a kész csőhálózatot és tudnom kell lépésről lépésre a folyamatot, miközben ki kell számolnom az ívek szögeit, és meg kell tudnom mellé az egyenes (passz-darabok) méretét is!
Szombaton délután, vagy vasárnap lesz szabadidőm, majd neki veselkedek a megfelelő kérdések megfogalmazásának!
Addig is köszönöm a segítőszándékot.
|
| Előzmény: [1843] Sinobi, 2014-06-19 23:59:29 |
|
| [1843] Sinobi | 2014-06-19 23:59:29 |
 Be tudod hatarolni a feladatokat arra a nehany, csak szamertekeikben eltero feladatra, amelyre szukseged lesz, vagy fel szeretnel keszulni arra, hogy barmilyen szobajoheto problemat meg tudj oldani?
Lesz majd lehetoseged internetet hasznalni? Internetre vagy szamologepre szukseged lesz.
Konkret kerdesre hogy valaszoljak: a szinusz egy fuggveny. Egy szog szinuszat sin(szog) alakban jeloljuk, es nagyon sokfelekeppen hivatkozunk ra szoban, de ha egy kifejezesben egy szog es a szinusz szo szerepel, ezt a jelolest ertjuk alatta. Egy altalad valasztott szog szinuszat, peldaul a 45°-et ugy kapod meg, hogy beirod a google-ba, hogy sin 45 degrees, es a google kiir egy masik szamot, amely a szog szinusza. Ez annyit jelent, hogy ha az atfogo 1 cm hosszu, es az atfogo es a vizszintes kozott a szog 45°, akkor a fuggoleges befogo 0.7071 cm hosszu. Mas szogre is, amit a google kiad, a fuggoleges befogo hosszat adja meg, 1 cm hosszu atfogo eseten.
|
| Előzmény: [1842] HajduM, 2014-06-18 22:09:22 |
|
| [1842] HajduM | 2014-06-18 22:09:22 |
 Mindenekelőtt köszönöm a választ...
Olyan hatással van ez rám, mintha nyakon öntöttek volna egy tányér forró nem kívánatos anyaggal, hogy finom legyek...
Olyan természetességgel ugrasz egyik értékről a másikra, ahogyan Én egyik állványról a másikra...
12 órás műszak után, szinte semmit nem értek ebből, de annyira, hogy még vissza kérdezi sem tudok..
Csőszerelő szakmai közegről van szó egyébként, ahol a 14 milliméter átmérőjű csőtől az 500-as ig dolgozunk, dominánsan nagyokkal.
Reggel elolvasom megint, és megpróbálok kérdést feltenni, mert most még az sem megy!
A Pitagoras tételt értem, de a többit nem, sem szinuszt, sem koszinuszt, sem semmit...
|
| Előzmény: [1841] w, 2014-06-17 22:56:24 |
|
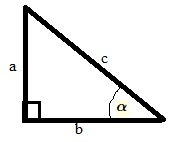
| [1841] w | 2014-06-17 22:56:24 |
 A szögfüggvényekkel kapcsolatban itt szerintem megtalálod a definíciókat. A kérdésekből ítélve, a számításokhoz csak a szögfüggvények definíciói, illetve még talán később a szinusz- és koszinusztétel kellenek, keress rájuk Google-on. Vagy vegyél egy trigonometriáról szóló alkalmas könyvet a könyvesboltban. A Kömal korábbi C-jelű feladatai között találhatók még példák bőséggel.
Nézzünk is egy a,b befogókkal rendelkező derékszögű háromszöget, melynek átfogója c. Az a befogóval szemben lévő szöget jelölje α.
Az első kérdésedben, ha jól értettem α és a adott. Ha megnézed, a definíció szerint sinα=ac, vagyis átszorozva c=asinα. A számológép segítségével sinα számolható, innen megvan c.
A második kérdésedhez annyit, hogy a Pitagorasz-tétel szerint a2+b2=c2 a Pitagorasz-tétel szerint, avagy például c=√a2+b2 stb. Vagyis egy derékszögű háromszögben két oldal ismeretében a harmadik oldal megadható. Utána nézd meg a sinα=ac hányadost, ennek az értéke ismert. Ahhoz, hogy ebből α-t megkapd, a sin függvény inverzét kell alkalmazni, számológépen pl. sin−1 szokta ezt jelölni. (Számológép nélkül ezek a számítások nem nagyon szoktak menni.)
A harmadik kérdésnél is ugyanezt csináljuk. Tudod, hogy például sinα=ac, vagy cosα=bc. Ezt átszorozva, c=asinα=bcosα. Vagyis az a befogót például 1sinα értékkel kell megszorozni, hogy c átfogót kapjuk, például α=45∘ esetén ez az arány sinα=1√2 miatt éppen √2 lesz. Vagy α=53∘-ra sin53∘=0,7986, 1sin53∘=1,2521.
|
 |
| Előzmény: [1840] HajduM, 2014-06-17 21:29:37 |
|
| [1840] HajduM | 2014-06-17 21:29:37 |
 Üdv mindenkinek. Az eddig olvasottakból azt feltételezem, hogy a kérdésem túl egyszerű lesz a fórum színvonalához, de valahonnan válaszhoz szeretnék jutni...
Tanultam persze régen ipari suliban sőt még általánosban is a szögfüggvényekkel kapcsolatosan, de ki emlékszik már arra, mikor az elmúlt 30 évben nem kellett alkalmaznom sehol ezt a tudást, így el is felejtődött...
Most olyan munkakörülmények közé kerültem, ahol egyre mélyebben bele kell másznom a rég tanultakba, de alig emlékszem valamire!
Ezért szeretnék a számotokra nyilván primitív kérdéseket feltenni, és persze válaszokat kapni rájuk!
Az első kérdésem.
Ismerem egy háromszög egyik befogójának méretét, és az ehhez tartozó szöget.
Pl, 45 fokos szög, és 600 milliméter a egyik befogó mérete. Szeretném megtudni az átló/átfogó méretét...
A második ennek a kérdésnek az inverze...
Tudom a két befogó méretét, és azt, hogy ezek 90 fokos szöget zárnak be, szeretném megtudni a vízszintes befogó és az átfogó által bezárt szöget...
A harmadik kérdés:
Tudjuk, hogy egy derékszögű háromszög esetén, ha pl az egyik befogó és az átfogó által bezárt szög 45 fok, akkor 1.42-vel szorozva a befogót, megkapjuk az átfogó méretét. Kérdés, hogy ugyanilyen szorzót, hogyan kaphatunk meg más, mondjuk 32 fok, vagy 53 vagy más szög esetén... Tehát egy méretből és az általa bezárt szögből miként számítható ki az az egyszerűsített szorzó, amely megadja az átfogó méretét?
Elnézést, ha kicsit sok és bugyuta a kérdésfelvetés, de per pillanat nem tudom jobban elétek tárni a kérdést...
|
|
| [1839] Sinobi | 2014-05-27 10:53:31 |
 eh, képlet helyesen:
⟹2d=|OAA(O)−k(O)||AA(O)|=|k(O)|r=const.
ábra:
|
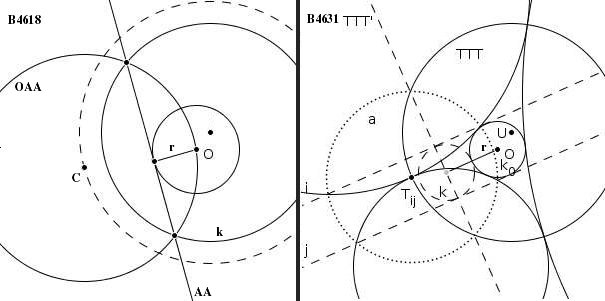 |
|
| [1838] Sinobi | 2014-05-27 10:49:49 |
 lemma: Ha adott k1, k2 kör, középpontjaik távolsága d>0, hatványvonaluk h, akkor a sík minden P pontjára:
|h(P)⋅2d|=|k1(P)−k2(P)|
Ahol h(X), k1(X) és k2(X) a megfelelő alakzatok normált egyenletei.
Ezt használva a B4618 megoldása:
B. 4618. Az A1A2... An sokszögbe és köré is írható kör. A beírt kör középpontja O, továbbá az OAiAi+1 kör középpontja Ci (i=1,2,...,n, és An+1=A1). Igazoljuk, hogy C1,C2,...,Cn egy körön vannak.
A sokszög K köré írt körére, az OAiAi+1 körre és az O pontra felírom az összefüggést.
OAA(O)=0, AA(O)=r, k(O)=const.
⟹2d=|k1(P)−k2(P)||AA(O)|=k(O)r=const.
⟹ Minden Ci ugyanolyan messze (|k(O)/2r|) van a sokszög köré írt kör középpontjától, Q.E.D.
B4631 megoldásának egy része:
B. 4631. Az egy síkban fekvő k0, k1, k2, k3 körök páronként kívülről érintik egymást; ki és kj érintési pontja Tij. Legyen k0 középpontja O; sugara r. Legyen a T12T23T31 kör középpontja U, sugara pedig R. Igazoljuk, hogy
|OU2−R2−r2|=4Rr
(ez saját átfogalmazásom az állításnak, valamivel könnyebb talán, mint amit ki akartak tűzni)
Elnevezem az egyik T pont körüli, k0-ra merőleges kört a-nak. a-ra történő inverzió során TTT kör k0 és az a kör hatványvonalába megy át, távolsága O-tól 2r (lásd ábra).
Az a és TTT körökre és az O pontra felírva a lemmát:
2R⋅2r=|TTT(O)−a(O)|=|OU2−R2−r2|
amelyből az eredeti feladathoz már csak az előjelet kell kiszedni valamilyen okos indoklással.
|
|
| [1837] HoA | 2014-04-21 20:51:09 |
 Re: ket olyan kor letezik, amely erinti az egyenespart es a korsor eleme, valahol ki kell diszkuszalni, hogy melyiket erinti CD
Lásd a [1834] feladatot.
|
| Előzmény: [1836] Sinobi, 2014-04-18 13:30:02 |
|
| [1836] Sinobi | 2014-04-18 13:30:02 |
 nem kap kedvet, de szerintem nagyon szep egyszeru a megoldasod, ha jol ertem:
T,O, kAB es kCD kozeppontja egy parallelogramman helyezkedik el, mert a kozeppontok a megfelelo oldalfelezo merolegesek metszespontjai, amelyek viszont tukrosek az OT felezopontjara, igy a kozeppontok is. Ha a parallelogramma ket oldalhosszanak osszegevel O korul kort rajzolunk, erinteni fogja kAB-t es kCD-t, tehat az ilyen kor egyszerre erinti oket. (nb: ket olyan kor letezik, amely erinti az egyenespart es a korsor eleme, valahol ki kell diszkuszalni, hogy melyiket erinti CD)
A T1 tartopontra torteno, k2-t fixen hagyo inverzio az elliptikus korsorbol koncentrikust kepez, k1 kepe k2-vel koncentrikus, es erinti AB kepet (kCD-t), tehat kAB-t, CD kepet is, QED.
Nekem ez tetzsik, egyszeru, elemi geometriai.
Az en megoldasom nem sokkal bonyolultabb, csak sajnos olyan dolgokat hasznal, amelyekhez nem ertek, es inkabb algebra mintsem geometria. Felveszem a k1-t erinto masik egyenest, es azt akarom belatni, hogy AC is atmegy T1-n. Ezt ugy teszem, hogy belatom, hogy a korsor egyenesparral valo Ai Ci metszespontjai egymassal projektivek, es belatom 4 specialis esetre, hogy az AC egyenes atmegy a T1-n. Nem bonyolult, de nem is erdekes, nem reszleteznem.
|
| Előzmény: [1835] HoA, 2014-04-14 21:54:31 |
|
| [1835] HoA | 2014-04-14 21:54:31 |
 Talán valaki kedvet kap foglalkozni a feladattal: Az én megoldásom [1832]-re az alábbi segédtételt használja. Lehet, hogy van egyszerűbb megoldás is.
Legyen az ABCD húrnégyszög körülírt köre k2 , ennek középpontja O , az átlók metszéspontja T. Az ABT pontokon át rajzolt kör kAB , a CDT pontokon át rajzolt kör kCD . Az O középpontú, kAB-t magába foglaló és érintő kör k1 . Ekkor k1 kCD-t is érinti.
|
| Előzmény: [1832] Sinobi, 2014-03-19 21:21:45 |
|
| [1834] HoA | 2014-04-09 08:48:49 |
 Még egy variáció [1832] témájára: Igazoljuk, hogy ha AB párhuzamos a körsor centrálisával, akkor CD áthalad a centrális és a hatványvonal M metszéspontján.
|
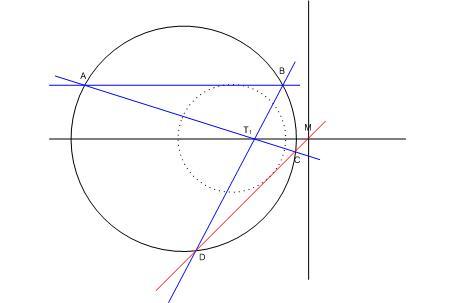 |
| Előzmény: [1832] Sinobi, 2014-03-19 21:21:45 |
|
| [1833] HoA | 2014-04-04 09:44:57 |
 Úgy látszik, mégsem olyan könnyű. Gondolatébresztőnek nézzünk egy speciális esetet: Legyen k1 a körsor másik tartópontja T2 (pontkör)
( Látom, már nálad sem működött a TeX értelmező. Tudja valaki, miért? )
|
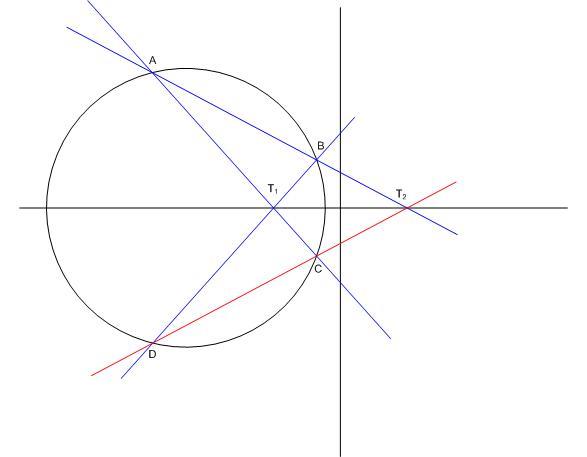 |
| Előzmény: [1832] Sinobi, 2014-03-19 21:21:45 |
|
| [1832] Sinobi | 2014-03-19 21:21:45 |
 > hogy számítások nélküli megoldás is van, de azt direkt nem olvastam el.
en a szamitasos megoldasokat ugrom at reflexbol :) Nem szereted a geometriat, vagy hogy?
Egy konnyebb: Adott egy elliptikus korsor k1, k2 kore, es az egyik, T1 tartopontja. A k1 kornek meghuzzuk egy t erintojet, hogy A B pontokban messe a k2 kort. Legyen C := AT1 ∩ k2, es D := BT1 ∩ k2. Igazold, hogy CD erinti k1-t!
|
 |
| Előzmény: [1825] w, 2014-03-03 08:06:55 |
|
|
|
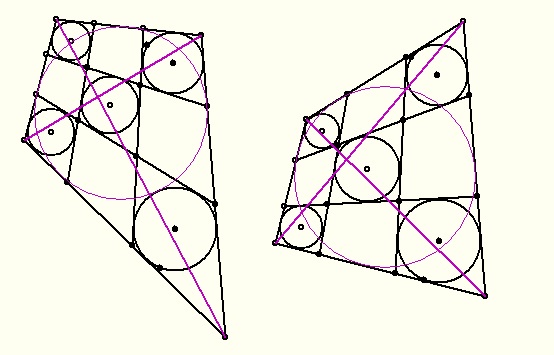
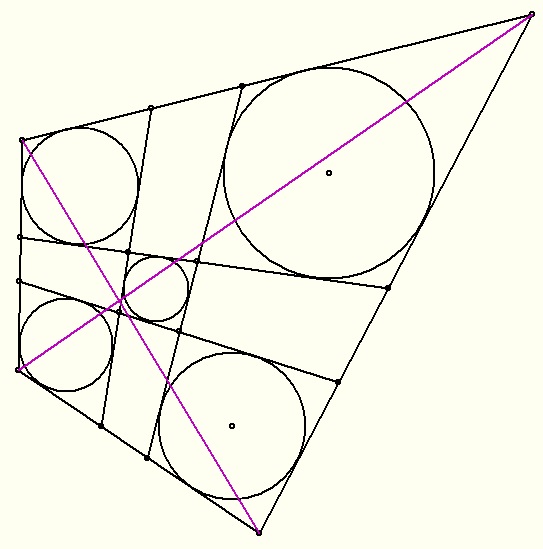
| [1829] BohnerGéza | 2014-03-08 03:19:01 |
 Az 1828-bani ábrám elkészítésénél a 4 kisebb körrel határoztam meg az egyeneseket, az ötödik négyszögbe pedig beleillett az 5. kör.
A szerkesztőprogrammal való játék azt valószínűsítette, hogy ha négy négyszög érintőnégyszög, akkor az 5. is, az átlókon lévő metszéspontok nem játszanak szerepet.
Esetleg új feltételt adnak, talán az eredeti feladatban a beírt körök középpontjai az átlókra esnek (a középső mindkettőre). (?)
Csak a szerkesztőprogrammal játszottam, magával a feladattal eddig keveset foglalkoztam.
|
| Előzmény: [1828] BohnerGéza, 2014-03-06 23:23:07 |
|
|
|