| [1876] Bátki Zsolt | 2014-10-02 20:43:53 |
 Nem mindent fogtam fel. Bennem lehet a hiba. A köbgyök 3 meggyőzőnek tűnik, mivel ezt javasoltam is. Itt egy új gondolatmenet. (Nem tudom, hogy kell rajzot küldeni) Vegyünk egy egység kört az origóban. Vegyünk fel egy D pontot rajta, ami a keresendő minimális távolságú A-tól és B-től. Vegyük fel az A-t az x tengelyen. Ekkor könnyen meghatározható az a félegyenes (f) D-ből indul és amin a B-nek kell lennie. Legyen 'e' egyenes ami az x koordinátával bezárt szöge háromszorosa a AOD szögnek, és az origóból indul. Nyilván az 'e' és 'f' metszéspontja jó megoldás a B pontra.
Tehát O,D,A ismeretében B szerkeszthető. (ebben a speciális esetben) De O,A,B esetén D nem szerkeszthető, mert ahhoz a AOB szöget harmadolni kellene tudni. Remélem világos volt és nem rontottam el semmit.
Tehát általános esetben nem szerkeszthető.
(az hogy általános szög nem harmadolható, az bizonyított, de nem egyszerű)
|
|
| [1875] csábos | 2014-10-01 22:54:59 |
 Mindig mondta a matektanárom, hogy a térszemléletem olyan, mint a döglött kacsáé.
Akkor számoljunk. cosϕ=a, sinϕ=√1−a2, t=1, u=12, v=2,w=3 helyettesítéssel a
tcos2ϕ+usin2ϕ=vcosϕ+wsinϕ
egyenletből
(2a2−1)+a√1−a2=2a+3√1−a2
lesz. Átrendezve
2a2−2a−1=(3−a)√1−a2
és négyzetre emelve, majd rendezve
5a4−14a3+8a2−8=0
adódik. Modulo 5 véve
a3+3a2−3
Ennek nincs gyöke modulo 5. Tehát a bővítés foka F5 fölött 3, így Q fölött a 3 többszöröse, tehát nem szerkeszthető.
|
| Előzmény: [1874] jonas, 2014-10-01 06:04:14 |
|
|
| [1873] csábos | 2014-09-30 20:55:52 |
 Nem értek valamit. Ha egyszer egyenlő szögeket keresünk, akkor miért nem invertáljuk az A pontot a körre (A1), majd a képet összekötjük a B-ponttal. Ahol metszi a kört (M-ben), ott a megfelelő szögek és tükörképeik is megegyeznek. Vagy megint elnéztem valamit?
|
| Előzmény: [1872] HoA, 2014-09-30 16:02:07 |
|
| [1872] HoA | 2014-09-30 16:02:07 |
 A nem-szerkeszthetőség irányában ( vázlat, ha valakit érdekel, részletezem )
Kínálja magát a komplex síkon tárgyalás. Válasszuk úgy a koordinátarendszert és a hosszegységet, hogy C legyen az origóban és D az egységsugarú körön. Ekkor d ( = CD ) egységvektor. Az egyenlő szögekből következik, hogy (( a -d ) / d) x (( b -d ) /d ) valós. Ebből d = eiϕ -vel ϕ -re
t⋅cos2ϕ+u⋅sin2ϕ=v⋅cosϕ+w⋅sinϕ
alakú egyenlet adódik, ahol az együtthatók az adatokból szerkeszthetőek. Már csak erről kéne megmutatni, hogy általában euklideszi módon nem szerkeszthető a megoldás.
( Ellenpélda: Két adott ponton átmenő, adott kört érintő kör középpontja : legyen itt is az adott egységsugarú kör középpontja, C az origóban, az érintési pont D, A és B a körön kívül. Ekkor d ( = CD ) egységvektor, a szerkesztendő kör középpontja O = kd ( k valós ) . Felírva az | A - O | = k - 1 ill. | B - O | = k - 1 egyenleteket , d = eiϕ -vel ϕ -re itt
v⋅cosϕ+w⋅sinϕ=z
alakú egyenlet adódik, ahol az együtthatók az adatokból szerkeszthetők, és mint ismert ekkor cosϕ -re másodfokú egyenletet kapunk szerkeszthető együtthatókkal. )
|
| Előzmény: [1868] Bátki Zsolt, 2014-09-23 18:19:23 |
|
|
| [1870] emm | 2014-09-25 02:58:38 |
 Hullafáradtan egy próbálkozás, 100%, hogy elszámolva, de valami ilyesmi: Legyen az ellipszis két fókuszpontja (c,0) és (−c,0), a kör sugara egységnyi, középpontja (u,v). Ekkor azt az a>c-t keressük (nagytengely), amire
x2(c2−a2)+y2a2=a2(c2−a2)
(x−u)2+(y−v)2=1
egyenletrendszernek 1 megoldása van. Vagyis:
x2(c2−a2)+y2a2=a2(c2−a2)((x−u)2+(y−v)2)
-nek egy megoldása van. Mivel ez a megoldás egyértelmű, ezért a diszkrimináns 0.
−4a2(a−c)(a+c)(−a2u2+c2u2−a2v2+a4v2+c2v2−a2c2v2+2a2vy−2a4vy−2c2vy+
+2a2c2vy+y2−2a2y2+a4y2+c2y2−a2c2y2)=0
Ez is egyértelmű y-ra, így a diszkrimináns ismét 0, így a-ra az egyenlet:
64(−1+a)a4(1+a)(a−c)3(a+c)3(−u2+a2u2−c2u2−v2+a2v2)=0
Aminek meg az értelmes megoldása
a=√(c2+1)u2+v2√u2+v2a=1
Ez meg szerkeszthető, ebből y=c2v2−u2−v2c2v megvanmá, megoldható, és megvan x=(u2+c2u2+v2)/(c2u) is. Nem egy szépségdíjas számolás, ilyenkor jó a számítógép.
|
| Előzmény: [1868] Bátki Zsolt, 2014-09-23 18:19:23 |
|
| [1869] marcius8 | 2014-09-24 12:18:21 |
 Egy ötlet: Legyenek az "e" ellipszis fókuszpontjai F1(+c;0), F2(-c;0), legyen az ellipszis félnagytengelye "a", legyen az ellipszis félkistengelye "b", ekkor az ellipszis egyenlete ismert. Legyen a "k" kör középpontja K(u;v) és sugara "r", ekkor a "k" kör egyenlete is ismert. Ami ismert: az "F1", "F2", "u", "v", "r". Az "a" értékét úgy kell meghatározni, hogy az ellipszis egyenletéből és a kör egyenletéből álló egyenletrendszernek pontosan egy (x,y) megoldáspárja legyen. Ekkor ezzel az "a" értékkel kiszámolva az (x,y) megoldáspárt, a kapott képlet alapján a metszéspont szerkeszthető.
Mi van, ha az "e" ellipszis úgy érinti a "k" kört, hogy a kör az ellipszis belsejében van.
Ez a probléma felkeltette az érdeklődésemet, még fogok vele foglalkozni. bertalan Zoltán.
|
| Előzmény: [1859] Bagesz, 2014-09-15 04:52:30 |
|
| [1868] Bátki Zsolt | 2014-09-23 18:19:23 |
 Az a sejtésem, hogy általánosságban euklidészi módon nem szerkeszthető. Ehhez találni kellene, egy elrendezést, amit algebrailag megoldva olyan szakasz jön ki, ami bizonyítottan nem szerkeszthető. pl köbgyök. A geogebra megenged pl szögharmadolást is ami eukledészi módon bizonyítottan nem megy. Az inverzió jó ötletnek tűnik. A feladat szépsége, hogy annyira egyszerű a felvetés, hogy érthetetlen evvel nem foglalkozott Senki, vagy mi nem tudunk róla ?
|
|
| [1867] Hajba Károly | 2014-09-19 20:31:37 |
 Erre azóta én is rájöttem. De ettől függetlenül a megoldást nagy valószínűséggel az inverzión keresztül lehet megtalálni.
Egy CAD-es programmal én is próbálok jó szerkesztést találni. A két pont és a tükörpont egy kört ad és az AB szakasz szakaszfelező merőlegese ill. a tükrözési tengely egy negyedik pontként ugyanezen körön metszik egymást. Pl az A és B pontot összekötő egyenes ill. az AB szakasz szakaszfelező merőleges inverziókörei alapján ezen kör inverziókörének két pontja már adott. Csak egy harmadik ismert pontra nem lelek rá.
|
| Előzmény: [1866] Bagesz, 2014-09-18 21:31:54 |
|
| [1866] Bagesz | 2014-09-18 21:31:54 |
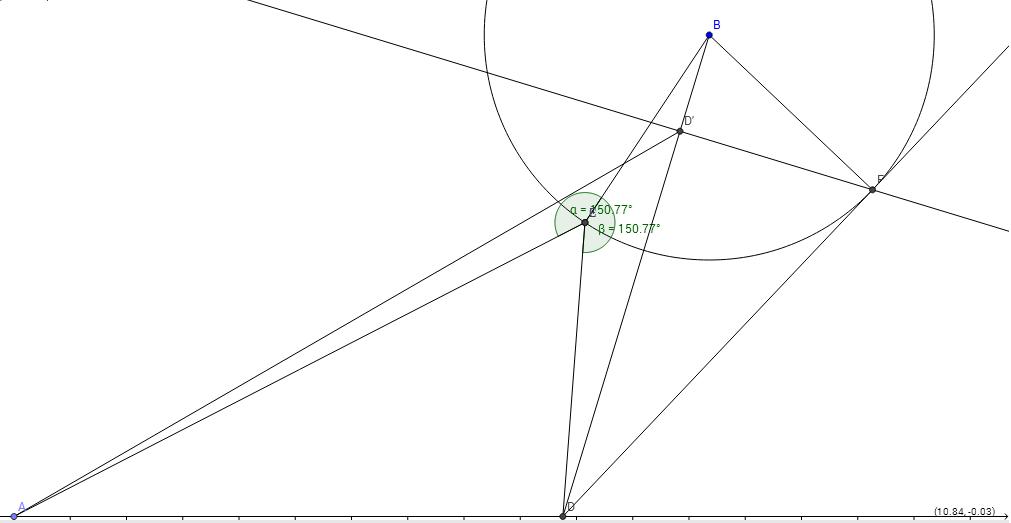
 Szia! Jó ötletnek tűnt ezért utána jártam a szerkesztésének. GeoGebrával el is készítettem, de sajnos nem a kívánt pontban metszette a kört. További ötleteket szívesen várok. Üdv, Bagesz
|
 |
| Előzmény: [1864] Hajba Károly, 2014-09-16 17:17:55 |
|
| [1865] Bagesz | 2014-09-16 22:26:02 |
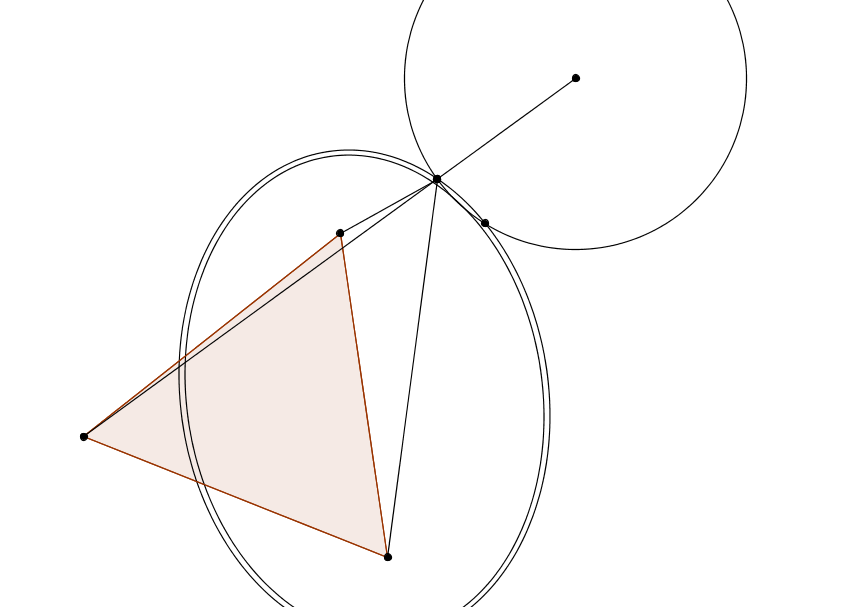
 A bizonyítás egyszerű, "A" és "B" pont közé kifeszítünk egy kötelet, ami kicsit hosszabb mint az "A" és "B" pont közötti távolság, Majd húzunk egy görbét úgy hogy feszes legyen a kötél mindvégig. Ez egy elipszis lesz. Majd egyre nagyobb kötelet veszünk, egyszer csak érinteni fogjuk a kört. Ez a pont a megoldás. Ezen a ponton az elipszis érintője és a két fókuszpontja által bezárt szög megegyezik, mint ahogy bármelyik pontja az elipszisnek és a két fókuszpontjával összekötő egyenes által bezárt szög.
|
 |
| Előzmény: [1860] Bátki Zsolt, 2014-09-15 22:28:23 |
|
| [1864] Hajba Károly | 2014-09-16 17:17:55 |
 Nem vagyok jártas a témában, de talán inverzióval (körre történő tükrözéssel) lehet a megoldást megtalálni.
Ki kellene próbálni, hogy az egyik pontot invertáljuk a körre és összekötjük a másikkal. Lehet, a metszéspont adja a megfelelő pontot a köríven.
|
| Előzmény: [1859] Bagesz, 2014-09-15 04:52:30 |
|
| [1863] Bátki Zsolt | 2014-09-16 13:57:23 |
 Bocsánat. Jó ötletnek tűnt. Jó, hogynem kezdtem el bizonyítani. A majdnem jó megoldás visz el igazán a lényegtől.
|
|
|
| [1861] Bátki Zsolt | 2014-09-15 22:32:53 |
 Persze a C nem az O a kör középpontja. Elírtam, de remélem értitek.
|
|
| [1860] Bátki Zsolt | 2014-09-15 22:28:23 |
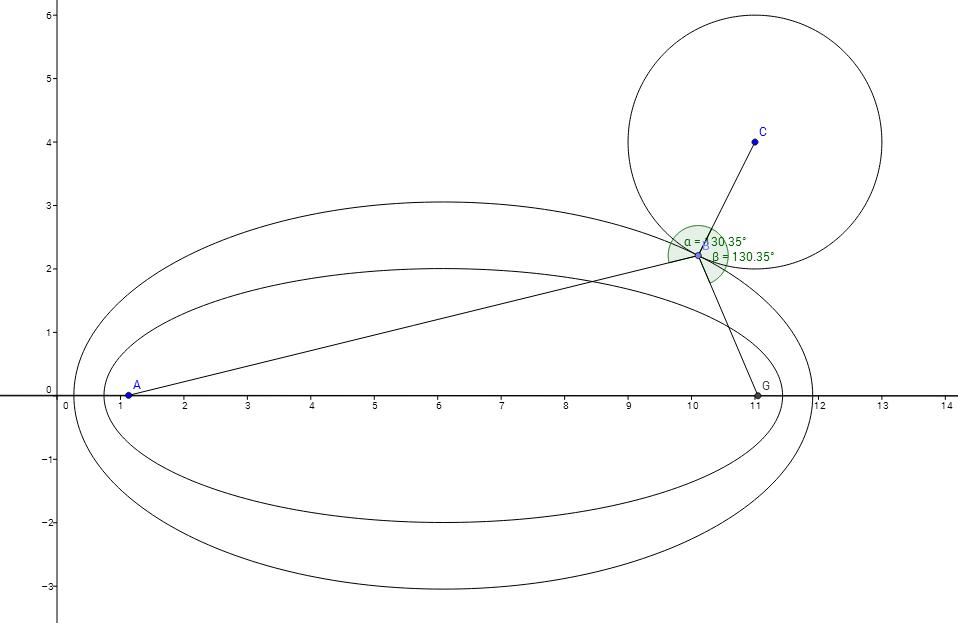
 Ha a két pont egyenese közrefogja a kört, akkor annak egyenese kimetszi a megoldást a körből.(háromszög egyenlőtlenség) AB>=AP+PB Ha AB szakasz kívül van a körön, akkor rajzoljunk egy szabályos háromszöget a körhöz képest kifelé. Ennek csúcspontja C. C és a kör középpontja O által meghatározott egyenes és a kör metszéspontja a nyerő. P pont. Nem tudom bizonyítani, de Geogebrával ellenőrizhető. Valószínűleg köze van ahhoz, hogy egy 120 fokosnál kisebb háromszög esetén AP+BP+CP összeg akkor a legkisebb, ha P minden oldalról 120 fokos szögben látszik. (Nem tudom kinek a tétele)
Így a szerkesztés nagyon egyszerű. Köszönöm a feladatot. megj, Fizika: a fény a legrövidebb utat keresi. Tehát ha tükörből van a kör (henger) akkor A-ból a B pontot P pontban látjuk. (Beesési és kimenő szög egyenlő) Aki akarja bizonyítsa, hogy tényleg ez a minimális. Érdekel a megoldás.
|
|
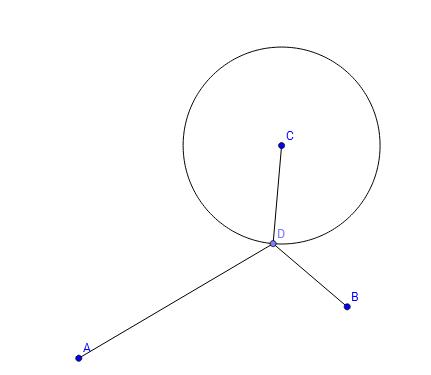
| [1859] Bagesz | 2014-09-15 04:52:30 |
 Sziasztok! Két pont között a legrövidebb utat kellene kiszámolnom, úgy hogy egy kört kell érinteni. Ismert a 2 pont és a kör koordinátái, valamint a kör sugara. Azt tudom, hogy a kör azon pontja a keresett pont, ahol a kör érintője és a pontok által bezárt szög megegyezik. Ezt viszont hogy lehet kiszámolni vagy kiszerkeszteni? Előre is köszi a segítséget. Üdv
|
 |
|
|
| [1857] Sinobi | 2014-08-10 20:25:29 |
 ennek kupszeletes altalanositasarol tudsz valamit? igaz-e, hogy 4-5 kupszelethez mindig letezik olyan kupszelet, amely mindegyiket erinti?
-
@w: "Legyen ABC háromszög BC oldalához írt köre h, amely a BC oldalt D-ben érinti. Tekintsük azt a k kört, amely áthalad a B és C pontokon, és érinti h-t (de nem a BC egyenes). Mutassuk meg, hogy h és k érintési pontját P-vel jelölve, PD egyenes felezi a BPC szöget."
Vesszuk BC Apolloniusz-korei kozul azt, amelyik meroleges h-ra. Athalad P-n es D-n, mert invertalva ra P es D fixen kell maradjanak.
|
| Előzmény: [1856] Fálesz Mihály, 2014-08-08 16:56:22 |
|
| [1856] Fálesz Mihály | 2014-08-08 16:56:22 |
 Ez az Apollóniusz féle szerkesztési feladat speciális esete: adott három kör, pont vagy egyenes, szerkesszünk olyan kört, ami mindhármat érinti (pont esetén átmegy rajta).
Egy tipikus megoldás, hogy a körök sugarait ugyanannyival megváltoztatjuk úgy, hogy az egyik kör ponttá fajuljon. (Az egyenest eltoljuk). Ezután jöhet egy inverzió, ami visszavezeti a feladatot két kör közös érintőinek megszerkesztésére.
|
| Előzmény: [1855] djuice, 2014-08-08 15:07:32 |
|
| [1855] djuice | 2014-08-08 15:07:32 |
 Sziasztok!
Az alábbi geometriai szerkesztési példán gondolkodom már napok óta, de nem jutok eredményre. Tudnátok segíteni?
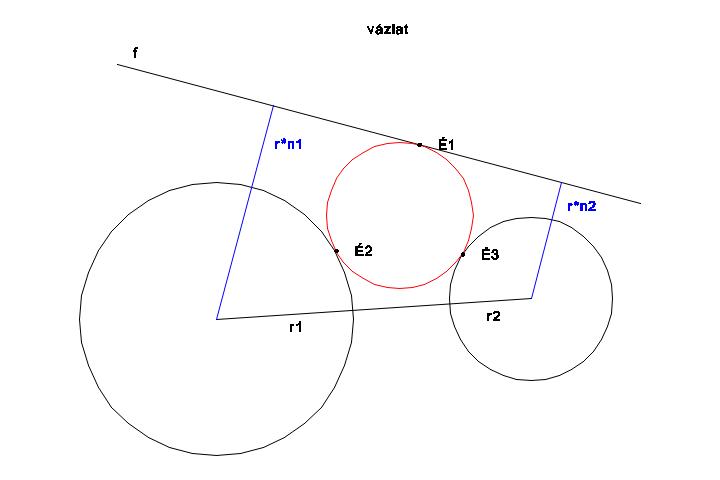
Adottak "r1" és "r2" tetszőleges sugarú és helyzetű körök a síkon, valamint egy őket nem érintő és nem metsző "f" egyenes, melynek ismerjük a körök középpontjától mért paraméteres (n1-; n2-szeres) távolságát. Szerkesszük meg azt a közbeeső kört, mely érinti mindkét kört és az egyenest! Számítani is próbálom a pontokat, de a szerkesztés volna a lényeg.
Mellékelem az ábrát is:
|
 |
|
|
| [1853] csábos | 2014-07-18 09:22:53 |
 Tekintsük azt a tetraédert, amely alapja az ABC háromszög és minden lapja egybevágó vele. Másképp: Induljon ki az A csúcsból egy a hosszú, a B csúcsból egy b hosszú, a C csúcsból egy c hosszú él. Ekkor a keresett pont a D csúcsból induló magasság talppontja.
MOTIVÁCIÓ: Oldjuk meg a feladatot térben. Ha a P (síkbeli pont) olyan, hogy a Q vetülete az ABC síkra P, akkor QA2=PA2+QP2, ugyanez szimmetrikusan. Így a QBC háromszög oldalainak négyzetösszege 2QP2-tel nagyobb, mint a PBC-é. A fent leírt D pont nyilvánvalóan teljesíti a feltételeket. Az, hogy nincs másik, az is kijön. Ha a P′ pont jó, akkor emeljük ki a síkból olyan ,,magasra", hogy a keresett összeg épp a2+b2+c2. Ekkor a feltételeket felírva adódik, hogy |Q′A|=a.
Síkban úgy oldanám meg, hogy keresném a P pont X tükörképét mondjuk az AC oldal felezőpontjára. Ekkor a PBC és PAB háromszögekre felírt négyzetösszegből PB2-t kivonva XC2+AB2=XA2+BC2 adódik, azaz a BCXA négyszög átlói merőlegesek. Innen az említett módokon adódik a P pont heyzete.
|
| Előzmény: [1852] w, 2014-07-17 18:56:13 |
|
| [1852] w | 2014-07-17 18:56:13 |
 OK igen.
Van egy analóg vektoros megoldás, azt a megoldást vártam (bár én tipikusan koordinátázom a feladatokat). Vagyis ha most a kisbetűk a megfelelő csúcsokhoz tartozó vektorok, akkor a feltétel szerint
(a−b)2+(b−x)2+(x−a)2=(a−c)2+(c−x)2+(x−a)2
és ennek ciklikus permutáltjai állnak fenn. Előbbi egyenletet kicsit alakítva, kapjuk, hogy (skalárszorzatokkal)
[(a2−2ab+b2)−(a2−2ac+c2)]+[(b2−2bx+x2)−(c2−2cx+x2)]=0,
2(−a+b+c−x)(b−c)=0,
azaz →AB+→XC vektor merőleges BC-re. Előbbi vektor A-ból az X pont BC felezőpontjára vett tükörképébe mutat, vagyis X rajta van az A-ból induló magasság BC felezőpontjára vonatkozó tükörképén. Hasonlóan, a B-ből és C-ből induló magasságok tükörképein is rajta van. Az egyetlen ilyen pont a kiegészítő háromszög magasságpontja.
Jellegétől fogva a feladatot szerintem nem nagyon lehet koordináták/vektorok nélkül megoldani. Kíváncsi vagyok, hogy mégis van-e "elemi" megoldása.
|
| Előzmény: [1851] emm, 2014-07-17 13:09:23 |
|