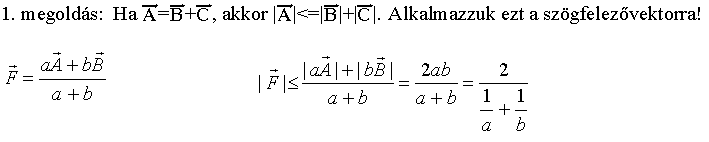Fórum: GEOMETRIA

[1] [2] [3] [4] [5] [6] [7] [8] [9] [10] [11] [12] [13] [14] [15] [16] [17] [18] [19] [20] [21] [22] [23] [24] [25] [26] [27] [28] [29] [30] [31] [32] [33] [34] [35] [36] [37] [38] [39] [40] [41] [42] [43] [44] [45] [46] [47] [48] [49] [50] [51] [52] [53] [54] [55] [56] [57] [58] [59] [60] [61] [62] [63] [64] [65] [66] [67] [68] [69] [70] [71] [72] [73] [74] [75] [76] [77] [78]

Szeretnél hozzászólni? Jelentkezz be.

[257] Lóczi Lajos

2005-06-29 20:44:07

Persze korrekt válasz az is, ha a szinusz-értéket kifejezed a megfelelő oldalhosszú és szögű derékszögű háromszögben a megfelelő oldalak arányával.

És még végtelen sok korrekt válasz létezik, amely sin (260^o) értékét más matematikai dolgokhoz, objektumokhoz kapcsolja.

Előzmény: [254] Stegi, 2005-06-28 18:50:34

[256] Lóczi Lajos

2005-06-29 20:38:19

A harmadfokú egyenlet itt sajnos épp olyan, hogy minden gyöke valós, de a megoldóképletében a komplex számok nem kerülhetők ki. (Ez a középkor óta már sokakat idegesített :-)

A három megoldás közül a minket érdeklő most ez:

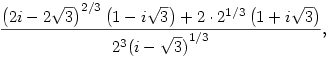
$\frac{\left(2 i-2 \sqrt{3}\right)^{2/3} \left(1-i \sqrt{3}\right)+2\cdot {2}^{1/3} \left(1+i \sqrt{3}\right)}{2^3 {(i-\sqrt{3})}^{1/3}},$

ahol i a komplex képzetes egység és a köbgyökök három lehetséges értéke közül ügyesen kell megválasztani a megfelelőt: a nevezőben szereplő komplex szám 1/3-ik hatványa az a komplex szám, melynek irányszöge 5 $\pi$ /18, nagysága 2^1/3, a számlálóban szereplő komplex szám 2/3-ik hatványa pedig az a komplex szám, melynek irányszöge 5 $\pi$ /9, nagysága pedig 2^.2^1/3 -- ahol természetesen 2^1/3 a "közönséges" valós köbgyök.

Ez tehát -sin (260^o) értéke. A fentiekből látszik, hogy ha ilyen formában, algebrai úton válaszolom meg a kérdést, akkor tulajdonképpen semmilyen "kezelhető", "kézzelfogható" információt nem mondtam a keresett szinusz-értékkel kapcsolatban. "A formula szép, de semmire sem jó."

Ellenben itt egy sokkal szebb és hasznosabb formula, az analízis nyelvén:

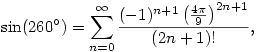
$\sin(260^\circ)=\sum_{n=0}^\infty \frac{(-1)^{n+1} \left(\frac{4 \pi }{9}\right)^{2n+1}}{(2 n+1)!},$

amiből tetszőleges pontossággal ki is lehet számolni a szinusz értékét.

Előzmény: [255] nadorp, 2005-06-29 16:01:16

[255] nadorp

2005-06-29 16:01:16

sin 260^o=-sin 80^o=-cos10^o.

Ismert, hogy cos 3 $\alpha$ =4cos³ $\alpha$ -3cos $\alpha$ ,azaz

cos30^o=4cos³10^o-3cos 10^o

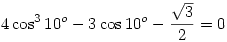
$4\cos^310^o-3\cos10^o-\frac{\sqrt3}2=0$

Ez egy harmadfokú egyenlet cos10-re, ami megoldható megoldóképlettel ( ezt már nem írnám le). Szerintem a feladatra ez a korrekt válasz, de nem tudom, hogy a harmadfokú egyenlet tananyag-e ott, ahol tanulsz. Ha középiskolás vagy, akkor úgy tudom nem, ha máshová jársz, akkor attól tartok igen.

Előzmény: [254] Stegi, 2005-06-28 18:50:34

[254] Stegi

2005-06-28 18:50:34

Sziasztok!

Nagyon egyszerű, mégsem tudom. Kérek segítséget. Ez egy vizsgakérdés : "Mennyi sin 260fok?" Mi rá a korrekt válasz?

Köszönom a segítséget.

[253] BohnerGéza	2005-06-13 10:11:08
Doom [247.] hozzászolásában lévő feladat megoldása. Az alábbi megoldásnál tekintsük C-t a helyvektorok kezdőpontjának!

Előzmény: [247] Doom, 2005-06-09 16:21:15

[252] BohnerGéza	2005-06-13 10:03:43
Doom feladatára 2. megoldás: Ha szögfelező, tükrözzünk rá!

Előzmény: [247] Doom, 2005-06-09 16:21:15

[251] Doom	2005-06-10 16:07:35
Köszönöm mindenkinek a sok megoldást! Fálesz 2. megoldása szerintem is nagyon ötletes! :)

[250] Fálesz Mihály

2005-06-10 07:38:40

Sziasztok,

Szerintem próbáljatok meg geometriaibb megoldásokat is kitalálni. Sok mindent ki lehet számolni, de az ilyen megoldások elrejtik a feladatok matematikai szépségeit, a kívülállónak meg azt a hamis képet mutatják, hogy csak ilyen megoldás van.

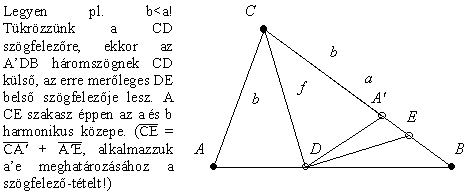
Érdemes lehet próbálkozni azzal, hogy a C csúcsból invertálunk. (Ez arra jó, hogy harmonikus közepet számtani középre cseréljük.) Utána már semmilyen számolás nem kell, csak egy ügyes segédpont, de ezt már találjátok ki Ti.

Mondanék két alternatív, kicsit számolós, de azért rövid utat is.

1. A szögfelezővektor a két oldalvektor súlyozott átlaga, a súlyokat a szögfelező-tételből megtdhatjuk. Aztán... (Valószínűleg innen jött a feladat is.)

2. Írjuk fel a CAB, CAF és CFB háromszögek területét az a,b,f szakaszokkal és a C-nél levő szögekkel.

Üdv.

F.M.

Előzmény: [249] levi, 2005-06-09 22:41:50

[249] levi	2005-06-09 22:41:50


Előzmény: [247] Doom, 2005-06-09 16:21:15

[248] Hajba Károly	2005-06-09 22:12:31


Előzmény: [247] Doom, 2005-06-09 16:21:15

[247] Doom

2005-06-09 16:21:15

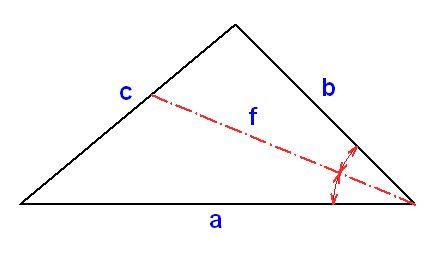
Bizonyítsuk be, hogy egy általános háromszög bármely 'f' szögfelezőjére igaz, hogy ha a vele szemköti oldal 'c', és a msáik kettő 'a' és 'b', akkor 'f' kisebb-egyenlő 'a' és 'b' harmonikus közepénél!

u.i.1: ha vki jól tud ábrát készíteni, nagyon megköszönném, ha csinálna hozzá egyet! :)

u.i.2: c-nem kell a feladat megértéséhez, de nem tudtam ábra nélkül máshogy elmagyarázni :(

[246] tudniakarok	2005-06-08 22:58:15
kritsmének emailben elküldtem még tegnap este a rólad elnevezett Fálesz Mihály tételét,és megfordítását,úgyhogy már nincs rá szüksége,sőt ma a válaszlevelében megköszönte a segítséget,ugyanis 1,7-es átlaggal átment matekból! Ezúton is Grat!
Előzmény: [245] Fálesz Mihály, 2005-06-08 12:35:40

[245] Fálesz Mihály

2005-06-08 12:35:40

Egy másik topikban kritsme szerette volna megtanulni a rólam elnevezett tételt.

A Thálész-tétel azt mondja ki, hogy egy kör átmérője a kör pontjaiból derékszögben látszik (kivéve persze az átmérő két végpontját, ahol baj van az egyik iránnyal), lásd az arcképemet.

A tételnek van megfordítása és egy kicsit erősebb változata is: az átmérő a körvonal pontjaiból derékszögben, a belső pontokból tompaszögben, a külső pontokból hegyesszögben látszik. Mindennek a bizonyítása sem nehéz. Kedves Kritsme! Melyikre van szükséged?

[244] tudniakarok	2005-06-08 01:15:31
Szerintem szabályos háromszöget alkotnak a súlypontok! (az eredeti ABC háromszögtől függetlenül)
Előzmény: [243] BohnerGéza, 2005-06-02 18:54:34

[243] BohnerGéza	2005-06-02 18:54:34
56. feladat: Az ABC háromszög oldalaira a CBA', az ACB' és a BAC' azonos körüljárású szabályos háromszöget írtuk. Ezek A", B", C" súlypontja milyen háromszöget határoz meg?

[242] BohnerGéza

2005-06-02 18:48:21

Megjegyzések az 50. és 51. feladathoz.

Az 50. feladattal kapcsolatban Hraskó András hívta fel arra a figyelmemet, hogy tulajdonképpen Pascal-tételre feladat. Teljesen igaz, ajánlom mindenki figyelmébe! Ha valaki kedvet érez hozzá, kérem írja be bővebben ezt a megoldást!

A [239.]-ben leírt megoldásnál a Pascal-tételes általánosabb, nem használja ki, hogy F a PR felezőpontja.

Az 51. feladatot az 50. [239] vázolt megoldás közben tulajdonképpen megoldottuk (, hivatkozva az 53. feladatra). Ha valaki kedvet érez hozzá, kérem írja be ennek a megoldását!

(Még ennyi segítség mellet sem könnyű feladatok!)

Előzmény: [239] BohnerGéza, 2005-05-19 19:03:44

[241] Hraskó András

2005-05-20 21:56:15

Kedves Géza!

Az 55. feladatban kitűzött szerkesztés, azt hiszem, teljes általánosságban nem végezhető el euklideszi módszerekkel.

Ha jól látom, akkor a háromszög a, b, c oldalai és beírt körének r sugara között az

r²s-(s-a)(s-b)(s-c)=0

összefüggés áll fenn (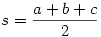 $s = \frac{a+b+c}{2}$ ). Ez c-re nézve (a-t, b-t és r-t tekintjük adottnak) harmadfokú egyenlet. A bal oldali polinom az a, b, r adatok megfelelő választása mellett a racionális számtest felett irreducibilis is, így a szerkeszthetőség elmélete (Galois elmélet) szerint c nem szerkeszthető.

[240] BohnerGéza	2005-05-19 22:54:58
Szívesen látnám - talán nem csak én - itt egy hozzáértő véleményét, hogy az 55. feladat adatai alapján szerkeszthető-e a háromszög.
Előzmény: [234] KiCsa, 2005-05-12 15:04:27

[239] BohnerGéza	2005-05-19 19:03:44
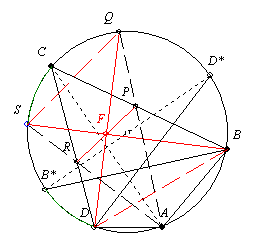
Az 50. feladat megoldása: Sajnos a [229.] ábráján a csúcsok betűzését elrontottam, így új ábra is készült. A megoldás vázlatát írom csak le, teret engedve az önálló munkának is. A megoldás lényege: Legyen F a PR felezőpontja. Megmutatjuk, hogy DBF szög = DBS szöggel = béta felével. Ez elég a feladat állításának igazolásához, hiszen analóg módon igaz, hogy BDF szög = BDQ szöggel. Az 53. feladatot felhasználva kapjuk, hogy DBF szög a béta fele. Mivel BBC szög a béta fele és CS ív=BD ívvel, ezért DBS szög is a béta fele.

Előzmény: [227] BohnerGéza, 2005-04-14 22:32:17

[238] tudniakarok	2005-05-13 15:15:10
Szép megoldás!Grat!
Előzmény: [235] secand, 2005-05-12 21:49:18

[237] secand	2005-05-12 21:51:38
És persze csak körzőt használtunk
Előzmény: [228] tudniakarok, 2005-04-20 22:03:19

[236] secand	2005-05-12 21:50:05
... ami valahogy így néz ki:

Előzmény: [228] tudniakarok, 2005-04-20 22:03:19

[235] secand	2005-05-12 21:49:18
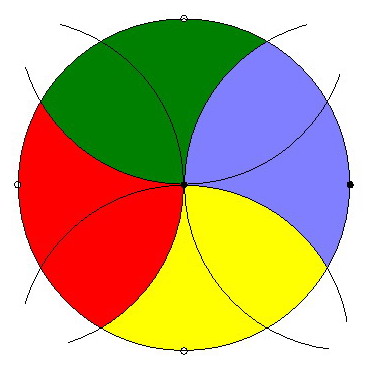
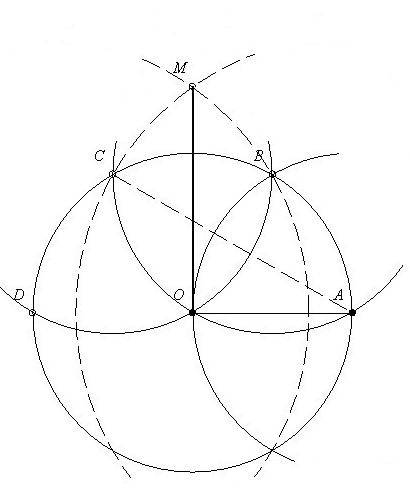
Megoldás az 52. feladatra: 1.ábra: Az O középpontú kör egy tetszőleges pontjából(:=A) körívezzünk a megadott sugárral a kör kerületére,így kapjuk a B,C,D pontokat!Az AC szakasz a körbe írható szabályos háromszög oldala,ezt körzőnyílásba véve,és körözve A illetve D pontokból metszéspontként kapjuk M pontot!Pit. tétellel belátható hogy az OM szakasz a körbe írható négyzet oldala,így már könnyen oszthaó a kör négy egyenlő ívre,ahonnan már csak néhány,a megadott sugárral való körzés választ el a négy területrésztől...

Előzmény: [228] tudniakarok, 2005-04-20 22:03:19

[234] KiCsa

2005-05-12 15:04:27

55. feleadat: Szerkesszünk háromszöget, ha adott két oldala és a beírt kör sugara!

Bocsánat ha lett volna.

[233] joe

2005-05-10 18:44:56

54. feladat: Legyen k egy félkör O középponttal és AB átmérővel. Legyen M a BA félegyenessel ellentétes félegyenes egy B-től különböző pontja. Az AB-től különböző p egyenes haladjon keresztül az M ponton és messe a k félkört két, egymástól különböző C és D pontban, miközben |MC| > |MD|. Legyen K az AOC és a BOD háromszögek köré írt köreinek O-tól különböző metszéspontja. Bizonyítsuk be, hogy OK merőleges MK-ra.

Már regisztráltál?
Új vendég vagy?