|
|
| [280] Szalkai István | 2005-09-14 13:42:39 |
 Kedves Mindenki !
A 2005.jan. feladatot általánosítva jutott eszembe a a következő probléma: Mi azon pontok mértani helye, amelyeknek adott egyenesektől való távolságai kielégítenek egy lineáris összefüggést? "Felfedezésem" biztosan nem új, bár irodalomban nem akadtam a nyomára. Közzéteszem mégis, hátha esetleg valakinek hasznára válik, no és biztosan én is tanulok hozzászólásaitokból! (Más fajta TEX-et használva nem sikerült a szöveget ide feltennem, de a következő linken megtalálható:
http://www.szt.vein.hu/~szalkai/Tavolsagok-jav.pdf
Üdvözlettel: szalkai@almos.vein.hu
|
|
| [279] BohnerGéza | 2005-08-27 00:19:34 |
 Jogos [275] jonas észrevétele, bár csak egy kis fogalmazási hibát követtem el. A zárójel szövege helyesen: valamint a talpponti háromszög területének. Igaz ez már nem nehéz, ha az előzőekre megvan a válasz.
|
| Előzmény: [275] jonas, 2005-08-23 22:40:10 |
|
| [278] lorantfy | 2005-08-24 10:25:21 |
 Hello Viktor!
Ez az EUKLIDES program. A 2.02 verzió ingyenesen letölthető: www.euklides.hu.
Töltsd le és szórakozz el vele. Én a kész ábrát Print Screen-el vágólapra szoktam tenni. Aztán egy képszerkesztővek kivágom a lényeges részt és átlátszóvá teszem, majd elmentem gif-ben és úgy csatolom a hozzászóláshoz. Így a háttérszínen jelenik meg.
|
| Előzmény: [277] xviktor, 2005-08-24 10:09:36 |
|
|
|
|
| [274] BohnerGéza | 2005-08-23 22:08:14 |
 Üdv mindenkinek!
Köszönöm Kós Ritának [273] a segítséget!
57. (számozott) feladat: Egy háromszög oldalai 13, 14 és 15. Adjuk meg a pontos értékét a
a.) beírt köre sugarának
b.) TcBTa (Ta és Tc magasságtalppontok) beírt köre sugarának
c.) TcBTa háromszög területének ( a talpponti háromszög területének )
|
|
| [273] Kós Rita | 2005-07-26 19:31:42 |
 A lekepezesek szorzatarol rovidebben-hosszabban Reiman Istvan konyveiben is van szo: Fejezetek az elemi geometriabol (Typotex, pici vekony, ebben biztosan), ill. A geometria es hatarteruletei c. konyvben, ha jol emlekszem.
|
| Előzmény: [272] BohnerGéza, 2005-07-15 23:09:11 |
|
| [272] BohnerGéza | 2005-07-15 23:09:11 |
 Az 50., 51., 53. és 56. feladat közös, általános megoldása.
Igen örülök lorantfy és Kós Géza 56. feladatra a [267]-ben ill. [268]-ban leírt megoldásának. Ezek is alkalmasak az általánosításra.
Ha valaki még nem ismeri a leképezések szorzatát, annak is megérthető amit írok, de időt és energiát kell rá szánnia, végigjátszva-gondolva minden állítást!
A téma bővebb megismeréséhez Rácz János könyveit tudom ajánlani, de ezek nehezen érhetők el. Rossz memóriám miatt további könyveket most nem tudok, remélem lesz valaki és kisegít!
Jelölje az A körüli alfa forgatást (A|alfa). Legyen
(1)...(C|gamma)*(B|béta)*(A|alfa)=I helybenhagyás.
//A leképezések szorzatát - egymás utáni elvégzését - visszafelé olvasva kell értelmezni, tehát először A, majd B, végül C körül forgatunk,// Helybenhagyást akkor kapunk, ha összesen n*360 fokot, ahol n egész, forgatunk és van fixpont. Ez a fent jelzett feladatok esetén áll. Az egyszerűség kedvéért és mert ilyen esetre ezen feladatok mindig visszavazethetők n=1 (vagy -1) esettel foglalkozunk.
Tudnunk kell még, hogy egy forgatás helyettesíthető két tengelyes tükrözés szorzatával, pl. (A-alfa)=t2*t1, ahol t1 és t2 is átmegy A-n, valamint t1 és t2 szöge alfa fele az irányítást is figyelembe véve. (1)-et balról (C|-gamma)-val szorozva:
(2)...(B|béta)*(A|alfa)= (C|-gamma)
Legyen t2=AB, t1 és t3 pedig olyan egyenesek, melyekre (A|alfa)=t2*t1 és (B|béta)=t3*t2. Ekkor
(3)...(B|béta)*(A|alfa)=(t3*t2)*(t2*t1)=t3*(t2*t2)*t1=t3*t1= (C|-gamma)
Tehát t1 és t3 is átmegy C-n. Mindent végiggondolva ABC olyan háromszög kell legyen, melyben a megfelelő csúcsoknál alfa/2, béta/2 ill. gamma/2 szög van. //Feltéve, hogy egyik szög sem n*360 fok, azaz mind a három forgatás valódi fogatás. //
Jó munkát a fent jelzett feladatok átgondolásához! Kitalálható esetleg újabb konkrét feladat is?!
|
| Előzmény: [268] Kós Géza, 2005-07-11 12:00:08 |
|
| [271] Hajba Károly | 2005-07-11 16:43:28 |
 Köszi a továbbképzés. Tényleg egyszerű.
De talán már nem olyan egyszerű azon zárt görbe megszerkesztése, mely görbe bármely pontjára azonos a PA+PB+PC hossz nagysága. Ezen görbe elfajult esete az I pont is.
HK
|
| Előzmény: [270] lorantfy, 2005-07-11 15:40:54 |
|
| [270] lorantfy | 2005-07-11 15:40:54 |
 Kedves Károly!
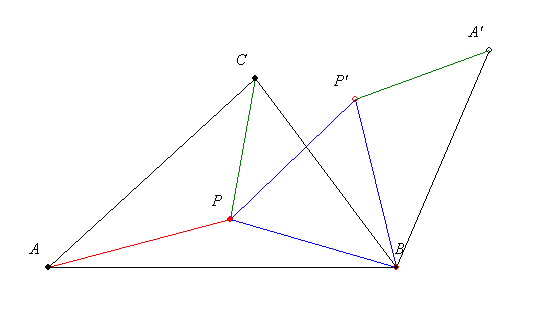
A tétel igaz: Ha az ABC hegyesszögű háromszög síkjában lévő P pontra igaz, hogy AP+BP+CP összeg minimális, akkor P a háromszög izogonális pontja (melyből mindhárom oldal 120 fokos szögben látszik.)
A bizonyítás nagyon szép és egyszerű. Forgassuk el a B pont körül a BCP háromszöget 60 fokkal. Mivel BP'P háromszög egyenlő oldalú, ezért az APP'A' törött vonal hossza megegyezik az AP+BP+CP összeggel. Az A' helyzete P-től független. APP'A' hossza akkor minimális, ha P és P' az AA' egyenesre illeszkedik. Ez pedig akkor van, ha APB és BPC és BPC 120o, vagyis ha P az izogonális pont. 120o, vagyis ha P az izogonális pont.
|
 |
| Előzmény: [269] Hajba Károly, 2005-07-11 13:31:23 |
|
| [269] Hajba Károly | 2005-07-11 13:31:23 |
 Üdv!
Érdekesnek tűnik a háromszög I pontja más szempontból is, mintha erre a pontra igaz, hogy PA + PB + PC hossz a legrövidebb, ahol A, B, C a háromszög csúcsai, míg P egy tetszőleges pont a síkjukban. Bizonyítani nem tudom, csak ráleltem. Ha igaz, gondolom egy -általam nem- ismert tétel.
Egy adtok egy kis továbbképzést vagy címeket, megköszönném. :o)
O.
|
| Előzmény: [268] Kós Géza, 2005-07-11 12:00:08 |
|
| [268] Kós Géza | 2005-07-11 12:00:08 |
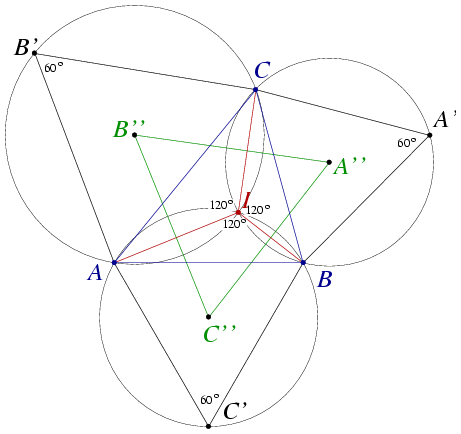
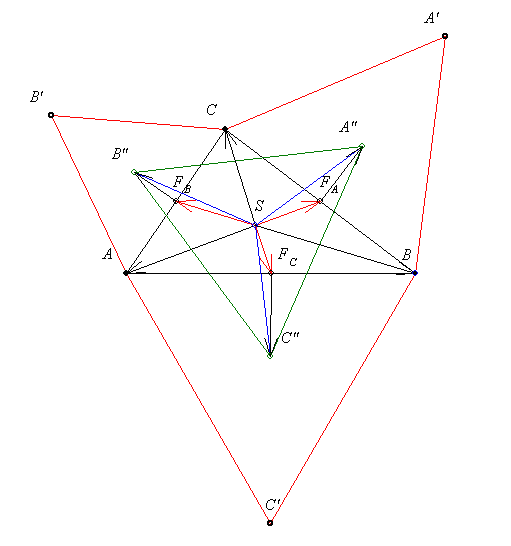
 Legyen az AC'B és BA'C köré írt körök B-től különböző metszéspontja I. Az AC'BI és BA'CI húrnégyszögek szögeiből AC'B =BA'C =BA'C =120o. Ebből következik, hogy CB'A =120o. Ebből következik, hogy CB'A =120o, vagyis az I pont a CB'A körön is rajta van. =120o, vagyis az I pont a CB'A körön is rajta van.
Ha az ABC háromszög mindegyik szöge 120 foknál kisebb, akkor I a háromszög izogonális pontja. Ha valamelyik szög éppen 120 fok vagy annál nagyobb, akkor nincs izogonális pont, és az ábra kicsit máshogy néz ki, de a három kör akkor is egy ponton megy át.
Az IA'', IB'', IC'' szakaszok (egyenesek) páronként 120 fokos (60 fokos) szöget zárnak be. Az A''B'', B''C'', C''A'' egyenesek két-két kör centrálisai, amik merőlegesen felezik az IA'', IB'', IC'' közös húrokat. Ezek az egyenesek tehát szintén páronként 60 fokos szöget zárnak be egymással.
|
 |
| Előzmény: [267] lorantfy, 2005-07-10 17:00:12 |
|
| [267] lorantfy | 2005-07-10 17:00:12 |
 Nem szeretném, ha Géza szép feladata feledésbe merülne!
56. feladat megoldása: Helyezzük a koord.rsz. origóját a háromszög S súlypontjába.
Legyen
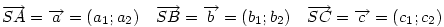
Fejezzük ki 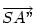 vektort ezek segítségével! vektort ezek segítségével!
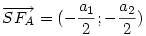
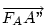 pedig pedig 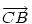 90 fokos, pozitív irányú elforgatottjának 90 fokos, pozitív irányú elforgatottjának 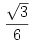 -szorosa. -szorosa.
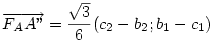
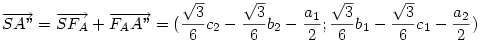
Hasonlóan:
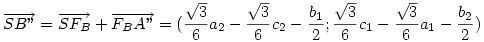
Az origó körüli 120 fokos, pozitív irányú forgatás mátrixa:
![\left[\matrix{cos 120^\circ &sin 120^\circ \cr -sin 120^\circ & cos 120^\circ \cr}\right]=
\left[\matrix{-\frac{1}{2}&\frac{\sqrt3}{2}\cr\frac{-\sqrt3}{2} &-\frac{1}{2} \cr}\right]](keplet.cgi?k=231A6CD88033A9CB)
Ezzel beszorozva 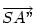 -t és felhasználva, hogy a,b,c vektorok összege 0, vagyis a koordinátákra is: -t és felhasználva, hogy a,b,c vektorok összege 0, vagyis a koordinátákra is:
a1+b1+c1=0, a2+b2+c2=0
 -t kapjuk. Tehát igaza van Dánielnek (=tudniakarok): valóban egyenlő oldalú háromszöget kapunk. -t kapjuk. Tehát igaza van Dánielnek (=tudniakarok): valóban egyenlő oldalú háromszöget kapunk.
|
 |
|
|
| [265] papi | 2005-07-06 08:54:13 |
 Bocsánat ! Természetesen az előbb Torricelli pontot akartam írni (papi)
|
|
| [264] papi | 2005-07-06 08:37:07 |
 Kedves Barátaim ! A h-szög nevezetes pontjainak a köré írható körre vonatkozó hatványait keresgélem. A S-pont, M-pont, beírt kör Kpontja és a Lamoine-féle pont esetében már rájöttem e hetványokra. De a Tossicelli-pontnál elakadtam. Tud valaki segíteni? (papi)
|
|
| [263] Lóczi Lajos | 2005-07-04 23:46:42 |
 Csak kiegészítésképpen írom, hogy a "négyzetes közelítés" az idézett Newton-módszerben persze nem azt jelenti, hogy a szereplő deriváltpolinom épp másodfokú, hanem azt, ahogyan a hiba nagysága csökken: a numerikus módszerek elméletéből ismert, hogy a Newton-módszer gyorsan konvergál, ha megfelelően közelről indítjuk a tényleges megoldástól (azaz z0-t "elég közel" választjuk meg a keresett értékhez, ami jelen esetben z0=1 mellett jó, de általában a pontos vonzási tartomány fraktálbonyolultságú alakzatokból áll, l. pl. http://mathworld.wolfram.com/NewtonsMethod.html)
A konvergencia a jelen esetben olyan gyors, hogy |z3-cos (10o)| 2.10-7, majd |z4-cos (10o)| 2.10-7, majd |z4-cos (10o)| 3.10-14, aztán |z5-cos (10o)| 3.10-14, aztán |z5-cos (10o)| 7.10-28, stb. 7.10-28, stb.
(A hatványsoros közelítés előnye, hogy a kezdeti értékkel nem kell bajlódni, de a konvergencia nem ennyire gyors: az n. lépésben a hiba ott n faktoriálissal arányos.)
|
| Előzmény: [261] jonas, 2005-07-02 10:28:45 |
|
|
| [261] jonas | 2005-07-02 10:28:45 |
 Az igaz, hogy a koszinusz (illetve a hatványsorba fejtése) többet mond az értékről, mint a komplex köbgyökös kifejtés.
Ennek ellenére a harmadfokú egyenlettel is lehet valamit kezdeni, ha már nadorp kiszámolta. Persze ha a megoldóképletet alkalmazzuk rá, akkor sinust kell számolni, de megoldhatjuk közvetlenül a harmadfokú egyenletet valamilyen közelítéssel. Nem nehéz négyzetes közelítést kapni:
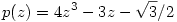
p'(z)=12z2-3
z0=1
zn+1=zn-p(z)/p'(z)
Ekkor zn cos (10deg)=0.98481 cos (10deg)=0.98481
|
| Előzmény: [256] Lóczi Lajos, 2005-06-29 20:38:19 |
|
| [260] Lóczi Lajos | 2005-06-30 10:50:02 |
 Rosszul emlékeztem, nem "tétel"-t, hanem "vizsgakérdés"-t említett. De ez már filozófia. Attól függ, milyen kontextusban van szükség a válaszra. Numerikus matematikai szempontból a táblázat tökéletes, de elméleti szempontból nem mindig.
|
| Előzmény: [259] Lóczi Lajos, 2005-06-30 10:43:26 |
|
| [259] Lóczi Lajos | 2005-06-30 10:43:26 |
 Én is ugyanazt mondtam, mint az első 2 bekezdésed, viszont pontosan megadtam, melyik értékre kell gondolni, tehát nem értem a problémát. És ez nem a megoldóképlet baja, hanem a köbgyöké, mint jelölésé, hiszen a komplex köbgyök nem is függvény. A valós négyzetgyök  -os megállapodásához hasonló megállapodást persze lehet tenni (és pl. a számítógépes programcsomagokban mindig van is ilyen), hogy a "köbgyök-jel" például mindig a (0 és 2 -os megállapodásához hasonló megállapodást persze lehet tenni (és pl. a számítógépes programcsomagokban mindig van is ilyen), hogy a "köbgyök-jel" például mindig a (0 és 2 közé eső) legkisebb irányszögű komplex számok jelentse, és akkor már nincs semmi gond a megoldóképletekkel. közé eső) legkisebb irányszögű komplex számok jelentse, és akkor már nincs semmi gond a megoldóképletekkel.
Viszont az, hogy kikeresel valamit egy táblázatból, szerintem sosem helyes válasz egy matematikai kérdésre, mert nem konstruktív és nem mutat rá a miértre, pláne nem bizonyítás (az eredeti kérdésben "tételt" említett a hozzászóló).
|
| Előzmény: [258] Fálesz Mihály, 2005-06-30 07:03:33 |
|
| [258] Fálesz Mihály | 2005-06-30 07:03:33 |
 A megoldóképlettel az is baj, hogy például az Általad felírt alak a gyököket az 50o+k.120o és a 100o+k.240o szögfüggvényeivel fejezi ki.
Szóval nem jutottunk közelebb, de most már 9, ugyanannyira felírhatatlan szám közül kell kiválasztani a 3 gyököt, amik közül csak az egyik sin 260o, a másik kettő hamis gyök...
Szerintem a helyes válasz az lett volna, hogy (a Függvénytáblából kiolvasva)
sin 260o=sin (180o+80o)=-sin 80o -0,9848. -0,9848.
|
| Előzmény: [256] Lóczi Lajos, 2005-06-29 20:38:19 |
|







 -re gondolt! Szerintem a=13, b=14, c=15 és a TCBTA
-re gondolt! Szerintem a=13, b=14, c=15 és a TCBTA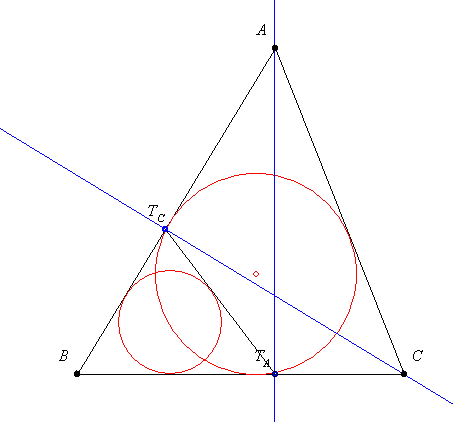



 és BPC
és BPC




 2.10-7, majd |z4-cos (10o)|
2.10-7, majd |z4-cos (10o)| cos (10deg)=0.98481
cos (10deg)=0.98481  -os megállapodásához hasonló megállapodást persze lehet tenni (és pl. a számítógépes programcsomagokban mindig van is ilyen), hogy a "köbgyök-jel" például mindig a (0 és 2
-os megállapodásához hasonló megállapodást persze lehet tenni (és pl. a számítógépes programcsomagokban mindig van is ilyen), hogy a "köbgyök-jel" például mindig a (0 és 2 közé eső) legkisebb irányszögű komplex számok jelentse, és akkor már nincs semmi gond a megoldóképletekkel.
közé eső) legkisebb irányszögű komplex számok jelentse, és akkor már nincs semmi gond a megoldóképletekkel. 
 -0,9848.
-0,9848.