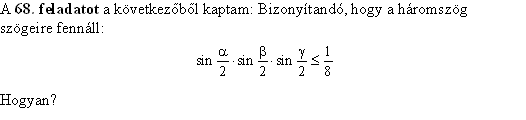| [410] Hajba Károly | 2006-04-12 07:38:44 |
 Kedves Géza!
Ha jól vettem az adást, akkor gyakorlatilag a szögek és térszögek közötti összefüggést, hasonlóságot az érintő ill. érintősík elfordulás, elmozdulás mértékében kell, lehet keresni.
Mégegyszer köszi a tájékoztatód.
|
| Előzmény: [405] Kós Géza, 2006-04-05 13:21:05 |
|
|
| [408] BohnerGéza | 2006-04-12 00:42:11 |
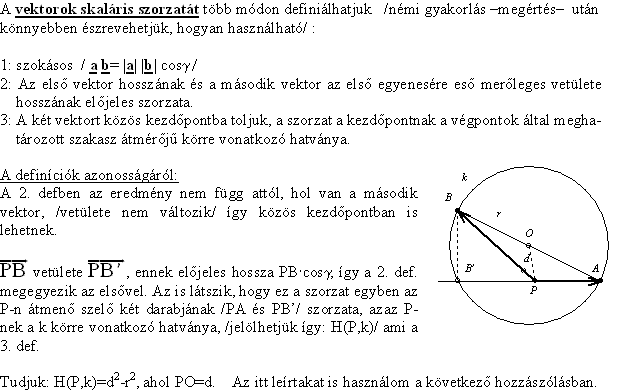
 A következő hozzászólásban használom az alábbiakat:
|
 |
|
| [407] Vonka Vilmos Úr | 2006-04-07 11:25:57 |
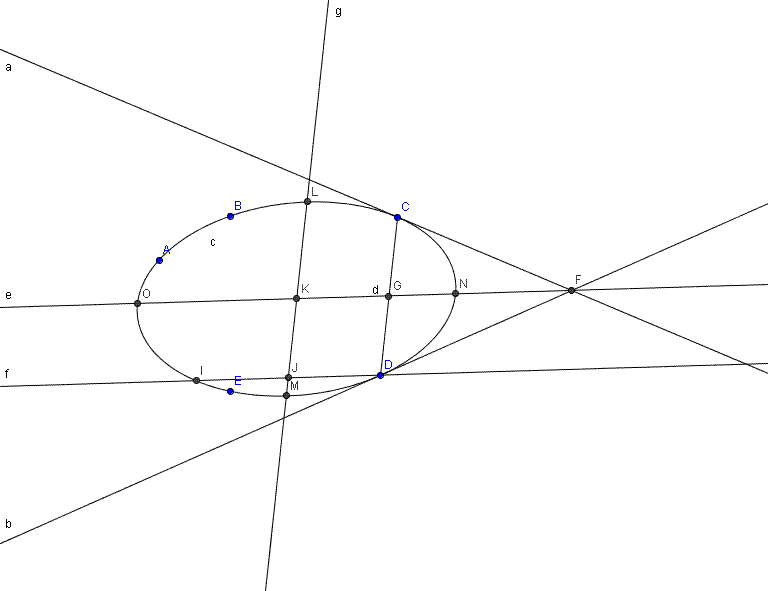
 Legyenek az ellipszis adott pontjai A, B, C, D, E!
1. A Pascal-tétel segítségével szerkeszthető pl. a C és D pontbeli érintő, ezek metszéspontját jelölje F!
2. Mivel F polárisa a CD egyenes, a CD irányához konjugált irányú átmérő áthalad az F ponton, valamint CD felezőpontján (G) is. Tehát FG (e) az ellipszis egy átmérő egyenese.
3. Legyen a D-n keresztül e-vel húzott párhuzamos egyenes f! A Pascal-tétel segítségével szerkeszthető f és az ellipszis másik metszéspontja (I). Az e-hez konjugált átmérő áthalad DI felezőpontján (J) és párhuzamos CD-vel: legyen ez a g egyenes.
4. A Steiner-szerkesztés segítségével megszerkeszthetőek e és g metszéspontjai az ellipszissel (LM, NO). Így megkaptuk az ellipszis egy konjugált átmérőpárját.
5. Egy konjugált átmérőpár ismeretében pl. Rytz-szerkesztéssel szerkeszthetőek az ellipszis tengelyei.
|
 |
| Előzmény: [406] Morci, 2006-04-06 21:59:18 |
|
| [406] Morci | 2006-04-06 21:59:18 |
 Üdv!
Segítséget szeretnék kérni. Netes keresőben itt dobott ki Pascal tétellel kapcsolatban infót, így gondoltam itt próbálok segítséget kérni.
Az a problémám, hogy egy ellipszis pontjai adottak, s nekem meg kell szekesztenem az ellipszist. A Pascal tétel alapján pontszámot tudok "bővíteni", illetve az itt talált ábra alapján még a nagytengely irányát is meg tudom határozni, viszont az ellipszis és a kör affin aránya ismeretlen, ezért nem lehet ezzel tovább lépni az ellipszis felől...
Van valamilyen módszer ellipszis szerkesztésére ha pár alkotó pontja adott csak?
Előre is köszönöm a segítséget!
|
|
|
| [405] Kós Géza | 2006-04-05 13:21:05 |
 Kedves Károly,
Már régóta tervezgetem, hogy egyszer majd kimerítőbben válaszolok a kérdésedre, de eddig nem jutottam hozzá. Lehet, hogy most is csak egy részét írom le.
A térben egy csomó dolog nem igaz úgy, mint a síkon, egyes dolgok pedig teljesen elvesznek. Pl. a síkon egy üres rácsháromszög, aminem a csúcsai rácspontok, de sem a kerületén, sem a belsejében nincsenek további rácspontok, mindig 1/2 területű. A térben a megfelelő állítás nem igaz, egy üres rácstetraéder térfogata akármilyen nagy lehet.
A szögek összegének létezik a térben megfelelője, de nincs szoros kapcsolata a csúcsoknál előforduló térszögek összegével. Ha például egy tetraédert kilapítasz úgy, hogy konvex négyszöggé fajul, a térszögek mindegyike 0-hoz fog tartani.
Ami a szögek összegének megfelel, az a görbület integrálja. A síkban egy egyszerű zárt töröttvonal esetén a külső szögek összege 2 , illetve egy kétszer folytonosan differenciálható egyszerű görbén a görbület ívhossz szerinti integrálja 2 , illetve egy kétszer folytonosan differenciálható egyszerű görbén a görbület ívhossz szerinti integrálja 2 . Ha a görbe/töröttvonal nem egyszerű, akkor az eredmény 2 . Ha a görbe/töröttvonal nem egyszerű, akkor az eredmény 2 -szer az irány körülfordulásainak száma. -szer az irány körülfordulásainak száma.
A térben egy elég sima, egyszerű zárt felületen a Gauss-görbület felszín szerinti integrálja mindig 4 . .
A poliédereket tekinthetjük sima felületek limeszének. pl. Minden élt lekerekítünk egy hengerpalásttal, a csúcsokat pedig gömbfelületekkel. (Most tekintsünk el attól, hogy ez nem mindig lehetséges, mondjuk szorítkozzunk a konvex poliéderekre.) A síklapokon és a hengerpalástokon a Gauss-görbület 0. A csúcsoknál a görbület integrálja a megfelelő gömbsokszög területe. A gömbsokszögeket összetolhatjuk egyetlen gömbbé, aminek a felszíne 4 . .
A gömbsokszögecskék területét másképp is kiszámolhatjuk.
Számoljuk össze egy csúcsnál a lapok szögeit. (Nem a lapsíkok közötti szögeket, hanem mindegyik lapnak az adott csúcsnál levő szögét.) Ha a szögek  1,..., 1,..., n, akkor a gömbsokszög szögei n, akkor a gömbsokszög szögei  - - 1,..., 1,..., - - n, a területe pedig 2 n, a területe pedig 2 -( -( 1+...+ 1+...+ n). Ha ezt az összes csúcsra kiszámoljuk és összeadjuk, akkor a csúcsok számát meg kell szoroznunk 2 n). Ha ezt az összes csúcsra kiszámoljuk és összeadjuk, akkor a csúcsok számát meg kell szoroznunk 2 -vel és ki kell vonnunk az összes lap összes szögének összegét. -vel és ki kell vonnunk az összes lap összes szögének összegét.
Legyen a csúcsok, élek, lapok száma C, E és L. Az egyes lapok éleinek száma legyen e1,...,eL. Ekkor persze e1+...+eL=2E, mert minden él két laphoz tartozik. Az i-edik lapon a szögek összege (ei-2) , az összes lap összes szögének összege tehát (e1-2) , az összes lap összes szögének összege tehát (e1-2) +...+(eL-2) +...+(eL-2) =(e1+...+eL-2L) =(e1+...+eL-2L) =(E-L)2 =(E-L)2 . .
A görbület integrálja a teljes felületen C.2 -(E-L)2 -(E-L)2 =(C-E+L)2 =(C-E+L)2 =4 =4 . .
A dolog egyrészt vicces, mert megjelenik a poliédertétel (C-E+L=2), ugyanakkor mindezt Gauss-görbület integrálása nélkül is tudtuk, és sem lap, sem térszögek nem jelentek meg...
|
 |
| Előzmény: [402] Hajba Károly, 2006-04-03 23:35:54 |
|
| [403] HoA | 2006-04-04 13:56:15 |
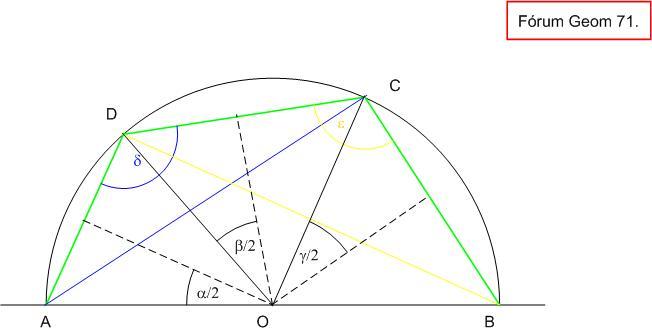
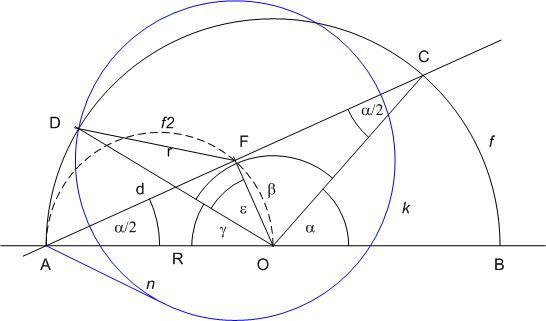
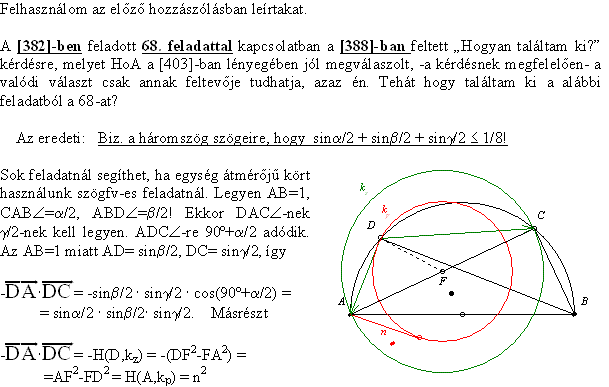
 A [388] egyenlőtlenség és a 68. feladat közötti kapcsolatról:
Legyen BOC  = = , COD , COD  = = , DOA , DOA  = = , , + + + + = = . Ekkor OAF . Ekkor OAF  = = /2 , DO = R ; FO = m = R*sin( /2 , DO = R ; FO = m = R*sin( /2), FA = d = R*cos( /2), FA = d = R*cos( /2), FOD /2), FOD  = = = = -( -( /2- /2- /2)= /2)= + + /2- /2- /2 /2
FD2=r2=DO2+FO2-2*DO*FO*cos =R2*(1+sin2( =R2*(1+sin2( /2)-2*sin( /2)-2*sin( /2)*cos /2)*cos ) )
n2=d2-r2=R2*(cos2( /2)-1-sin2( /2)-1-sin2( /2)+2*sin( /2)+2*sin( /2)*cos /2)*cos )=R2*(-2*sin2( )=R2*(-2*sin2( /2)+2*sin( /2)+2*sin( /2)*cos /2)*cos )= )=
2R2*sin( /2)*(cos /2)*(cos -sin( -sin( /2)) . /2)) .
A [388] egyenlőtlenségben válasszuk úgy a betűzést, hogy    teljesüljön és ennek megfelelően legyen D közelebb A-hoz mint C-hez. Ekkor teljesüljön és ennek megfelelően legyen D közelebb A-hoz mint C-hez. Ekkor  = = + + /2- /2- /2 /2  /2+ /2+ /2+ /2+ /2- /2- /2=0 , cos /2=0 , cos =sin( =sin( + + /2) , n2=2R2*sin( /2) , n2=2R2*sin( /2)*(sin( /2)*(sin( + + /2)-sin( /2)-sin( /2)) /2))
Felhasználva a sin(u+v) - sin(u-v) = 2*cos(u)*sin(v) azonosságot
n2=4R2*sin( /2)*cos(( /2)*cos(( + + )/2)*sin( )/2)*sin( /2)=4R2*sin( /2)=4R2*sin( /2)*sin( /2)*sin( /2)*sin( /2)*sin( /2) /2)
|
 |
| Előzmény: [388] BohnerGéza, 2006-03-14 12:02:36 |
|
| [402] Hajba Károly | 2006-04-03 23:35:54 |
 Üdv!
A Wolfram-on kicsit kutakodva ill. az SH Atlaszban találtam még néhány dolgot, de egy kicsit elgondolkoztam én is a témán. (Magad uram, ha szolgád nincsen.:o)
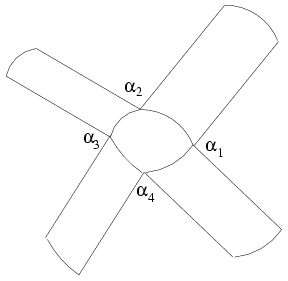
Ismert, hogy egy gömbháromszög területe 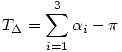 . Ezen minimális gömbi sokszöghöz adott szomszédos pontpárjukat egyesítve újabb háromszög illeszthető. Így tetszőleges n-sokszög állítható elő, akár konkáv is. Ezen sokszög területe, melyet nem nehéz belátni, . Ezen minimális gömbi sokszöghöz adott szomszédos pontpárjukat egyesítve újabb háromszög illeszthető. Így tetszőleges n-sokszög állítható elő, akár konkáv is. Ezen sokszög területe, melyet nem nehéz belátni, 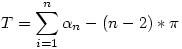
Ezen gömb középpontjából kiinduló és a sokszög pontjaira illesztett félegyenesek a pontok sorrendje szerint a félegyenesek közötti síkok által meghatározott térrész a T-vel arányos térszöget határoz meg.
A gömbi sokszög adott csúcspontjára illesztett és a gömböt érintő sík a csúcsba befutó két gömbi egyenes és gömbközéppont által meghatározott két síklapra merőleges. Ezért a két síklap által bezárt szög azonos a csúcsponti szöggel.
Fentiekből következik, hogy egy síkidom adott csúcspontjához tartozó szomszédos lapok által meghatározott szögek összege és a lapok által meghatározott térszög mértéke között szoros összefüggés áll fenn a fenti képlet szerint.
Újabb érdekes összefüggések adódnak egy idom lapszögeinek és térszögeinek összegei között, de erről később, ha addig valaki nem tesz be egy ezirányú összefoglaló linket. Mert biztos van erről irodalom, legfeljebb még nem bukkantam rá.
|
| Előzmény: [398] Lóczi Lajos, 2006-03-29 22:21:15 |
|
|
| [400] Hajba Károly | 2006-03-30 14:21:40 |
 Köszi. Amit nyelvtudás nélkül ki lehet belőle hámozni, azt eddig is sejtettem.
Gyakorlatilag az érdekelne, hogy a síklapú testek csúcsaihoz tartozó térszögek összege milyen szabályosságot mutat. Mennyire analóg ill. milyen módon analóg a 2D-s szabályokkal.  Egy-egy csúcshoz tartozó síkszögek és térszög között milyen összefüggések állnak fenn. Egy-egy csúcshoz tartozó síkszögek és térszög között milyen összefüggések állnak fenn.
Azt gyanítom, hogy azonos csúcsszámú testekhez nem feltétlenül azonos nagyságú térszög összeg tartozik. Talán a csúcshoz tartozó síkszögek valamiféle összesítése állandó, vagy esetleg a síklapok által közrezárt szögek összege?
|
| Előzmény: [398] Lóczi Lajos, 2006-03-29 22:21:15 |
|
| [399] BohnerGéza | 2006-03-30 08:02:53 |
 Köszönöm HoA-nak és Jenei Attilának a 68. ill. 70. feladatra adott megoldásait! Még eggyel bővítem a kapcsolódó feladatokat:
71. feladat: Az adott AB átmérőjű félkörön a 68. feladat ábrájának megfelelő sorrendben ([385] hozzászólás) helyezkedik el a C és D pont. Hol vannak ezek, ha a BC*CD*DA maximális?
|
|
|
| [397] Hajba Károly | 2006-03-27 13:21:05 |
 Üdv!
Egy kis elméleti fejtágításra lenne szükségem a térszögek terén. Az alapfogalmak (térszög, szteradián) meghatározásán kivül nem sok mindent ad ki a Kugli.
Előre is köszönök minden segítséget ill. magyarnyelvű linket.
|
|
| [396] HoA | 2006-03-24 14:34:56 |
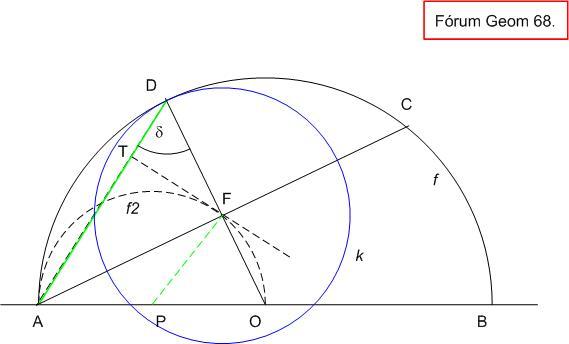
 Kedvet kapva Jenei Attilától egy cosinus tételes megoldásra, mégegyszer a 68. feladatról : Odáig, hogy k belülről érinti f-et ld. a 386-os hozzászólást. Legyen az f2 félkörív középpontja P. AD-t rögzítve n2=AF2-FD2=AD2-2*AD*FD*cos =AD(AD-2*FD*cos =AD(AD-2*FD*cos ) . Mivel D az f2 köríven kívül van, ) . Mivel D az f2 köríven kívül van,  hegyesszög, a kifejezés akkor a legnagyobb, ha DT=FD*cos hegyesszög, a kifejezés akkor a legnagyobb, ha DT=FD*cos , FD merőleges vetülete AD-re a legkisebb. Ez pedig akkor áll elő, ha FT az f2 körív AD-re merőleges érintője. De ekkor PF || AD, POF és AOD , FD merőleges vetülete AD-re a legkisebb. Ez pedig akkor áll elő, ha FT az f2 körív AD-re merőleges érintője. De ekkor PF || AD, POF és AOD  -ek hasonlóak, PF = PO -> AD = AO, vagyis AD az f félkörben sugár hosszúságú húr. -ek hasonlóak, PF = PO -> AD = AO, vagyis AD az f félkörben sugár hosszúságú húr.
|
 |
| Előzmény: [395] jenei.attila, 2006-03-22 11:48:06 |
|
| [395] jenei.attila | 2006-03-22 11:48:06 |
 A szóbanforgó érintési pont legyen E.
BE2=BD2-DE2=BD2-DC2=AB2-AD2-DC2
Ezért BE akkor maximális, ha AD2+DC2 minimális.
AD2+DC2=AC2+2*AD*DC*cos 
. Mivel AC állandó és cos  állandó és negatív AD*DC-nek kell maximálisnak lenni. Vagyis mivel sin állandó és negatív AD*DC-nek kell maximálisnak lenni. Vagyis mivel sin  állandó és pozitív az ADC háromszög területének kell maximálisnak lenni. Ez pedig akkor maximális, ha D az AC ív felezőpontja. Nem használtuk ki, hogy C az AB ív felezőpontja. állandó és pozitív az ADC háromszög területének kell maximálisnak lenni. Ez pedig akkor maximális, ha D az AC ív felezőpontja. Nem használtuk ki, hogy C az AB ív felezőpontja.
|
| Előzmény: [389] BohnerGéza, 2006-03-17 07:55:20 |
|
|
| [393] HoA | 2006-03-21 09:55:50 |
 A 70. feladat-ra van egy, a 68-ashoz hasonló trigonometriai megoldásom, ha nem lesz jobb, beírom. De szívesen látnék erre is meg a 68-asra is egy nem trigonometriait.
|
| Előzmény: [389] BohnerGéza, 2006-03-17 07:55:20 |
|
| [392] HoA | 2006-03-21 09:50:54 |
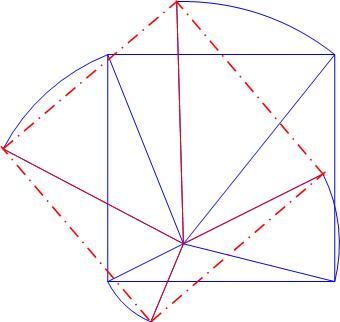
 Ha arra gondolsz, hogyan kell elforgatni egy négyzetet a síkjában fekvő adott pont körül adott szöggel - és ekkor mindegy, a pont a négyzeten belül vagy kívül van - egy megoldás az ábra szerinti: az adott pontból a négyzet csúcsaiba húzott szakaszok mindegyikét elforgatjuk az adott szöggel. Az új végpontok az elforgatott négyzet csúcsai.
|
 |
| Előzmény: [391] tothszivike, 2006-03-20 19:00:39 |
|
| [391] tothszivike | 2006-03-20 19:00:39 |
 Segítséget szeretnék kérni! Hogyan kell elforgatni egy négyzetet egy azon belüli ponton keresztül mert nekük az osztályban mindenkinek trapéz jött ki a tanárnő meg nem hajlandó megmutatni!
|
|
| [389] BohnerGéza | 2006-03-17 07:55:20 |
 A 384. hozzászólásban HoA által felvetett kérdés miatt alakult ki a következő feladat:
70. feladat: Az AB átmérőjű félkörív felezőpontja C. D az AC íven mozoghat. Mikor lesz leghosszabb a B-ből a D középpontú, C-n átmenő körhöz húzott érintőszakasz?
|
|
|
| [387] axbx | 2006-03-13 20:48:33 |
 Nem megy nékem az geometria..
|
|
| [386] HoA | 2006-03-10 16:17:31 |
 Köszönöm az ábrát.
Legyen az AB átmérőjű f félkör középpontja O, sugara R. F rajta van f A-ból vett 1/2 arányú kicsinyítésén vagyis az AO átmérőjű f2 félkörön. n hossza A pont k-ra vonatkozó hatványának négyzetgyöke. Az AF távolságot d-vel, k sugarát r-rel jelölve n2=(d+r)(d-r)=d2-r2 . C-t - és ezzel F-et és d-t - rögzítve ez akkor a legnagyobb amikor r a legkisebb, vagyis amikor k belülről érinti f-et. Ekkor D az OF egyenes és f metszéspontja, jelöljük Dm-mel.
C-t az f félkörön mozgatva, C és F helyzetét a 0 és 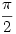 közé eső BAC = OAF = közé eső BAC = OAF =  szöggel jellemezve, mivel F rajta van OA Thalesz-körén szöggel jellemezve, mivel F rajta van OA Thalesz-körén
d=Rcos ,r=R(1-sin ,r=R(1-sin ) )
n2=R2(cos2 -(1-sin -(1-sin )2)=R2(cos2 )2)=R2(cos2 -1-sin2 -1-sin2 +2sin +2sin )=R2(cos2 )=R2(cos2 -cos2 -cos2 -sin2 -sin2 -sin2 -sin2 +2sin +2sin )= )=
=2R2(sin -sin2 -sin2 )=2R2(sin )=2R2(sin )(1-sin )(1-sin ) )
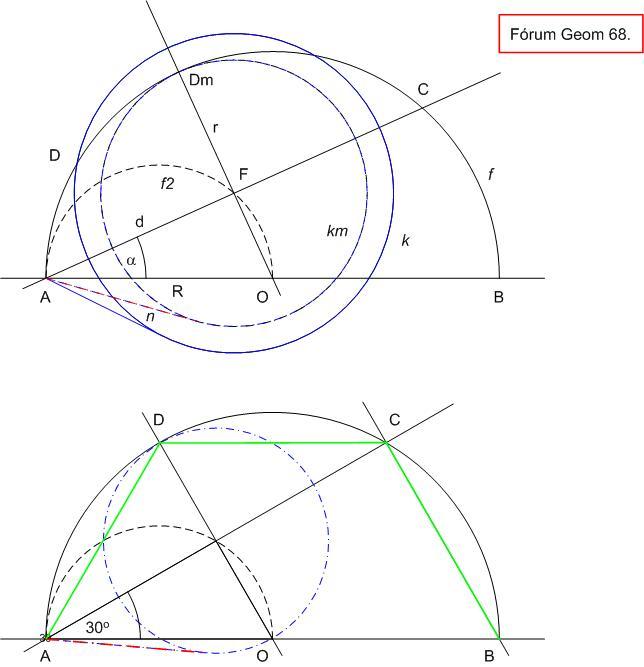
Ez pedig a számtani és mértani közép egyenlőtlenség miatt akkor a legnagyobb, ha sin =1-sin =1-sin =1/2 Ez a vizsgált tartományban =1/2 Ez a vizsgált tartományban  =30o -nál következik be. Így DOA szög = CBA szög = 60o , A, D, C és B pontok egy szabályos hatszög egymás utáni csúcsai. sin =30o -nál következik be. Így DOA szög = CBA szög = 60o , A, D, C és B pontok egy szabályos hatszög egymás utáni csúcsai. sin =1/2 -t helyettessítve =1/2 -t helyettessítve 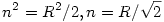
|
 |
| Előzmény: [385] BohnerGéza, 2006-03-09 20:26:52 |
|
|









 , illetve egy kétszer folytonosan differenciálható egyszerű görbén a görbület ívhossz szerinti integrálja 2
, illetve egy kétszer folytonosan differenciálható egyszerű görbén a görbület ívhossz szerinti integrálja 2 1,...,
1,...,

 =
= , DOA
, DOA  ,
, =
=

 területe, hiszen
területe, hiszen  és így sin
és így sin