| [436] epsilon | 2006-06-10 10:04:38 |
 Kösz, kiindulási ötletnek nem rosz! ;-)
|
|
| [435] jonas | 2006-06-09 22:53:35 |
 Indulj ki abból, hogy a négy sarokhoz négy különböző négyzetnek kell tartoznia, és azon kívül csak egy négyzeted van. Innentől három lehetőség van:
Az első kettőnél a nagy téglalap nem lehet négyzet, a harmadiknál a kis téglalapok. Persze ez nem precíz bizonyítás.
|
| Előzmény: [434] epsilon, 2006-06-09 22:21:08 |
|
| [434] epsilon | 2006-06-09 22:21:08 |
 Igen, ismerem a könyvet, nagyon kedves,és tanulságos! Sok helyen kerestem az 5-re egy szimpatikus bizonyítást, most meg az is felbuzdított, hogy a Kengurú egyik selejtezőjén feltették a kérdést, hogy hány darabra nem darabolható egy négyzet, és persze ott volt az 5 is, ez azt a gyanút keltette bennem, hogy ha ilyen helyen tippelés formájában adták föl, akkor csak kell lennie valamilyen egyszerű bizonyításnak! Hátha valaki találkozott ilyennel?!
|
|
| [433] jonas | 2006-06-09 21:42:58 |
 Igen, akárhány négyzetre feldarabolható. A bizonyítás megtalálható Reiman István könyvének 15. fejezetében. Ez azon áll, hogy bármely darabolásból kaphatsz egy 3-mal több négyzetté darabolást, ha az egyik kis négyzetet négy felé osztod, így elég megmutatni, hogy a négyzetet 4, 6, és 8 felé lehet vágni. Az 5 négyzetes esetre nem ad egyszerű bizonyítást.
|
| Előzmény: [432] epsilon, 2006-06-09 19:41:05 |
|
| [432] epsilon | 2006-06-09 19:41:05 |
 Helló! Nagyon szimpatikus feladat a négyzetnek az akárhány négyzetre darabolása, ez az "akárhány" természetesen 4 vagy több mint 5. Régóta felmerült bennem a kérdés, hogy van-e egyszerű bizonyítás arra, hogy egy négyzet nem darabolható fel 5 darab négyzetre? Ha van véleményetek, bizonyításotok szívesen várom! Üdv: epsilon
|
|
| [431] Csimby | 2006-06-05 01:23:39 |
 Szabó László: Konvex Geometria (Egyetemi jegyzet) Az ELTE TTK Déli épületében a 4. emeleten a geometria tanszék titkárságán lehet kapni, ha jól emlékszem kb. 500 ft.
|
| Előzmény: [430] tyuki, 2006-06-03 17:18:03 |
|
| [430] tyuki | 2006-06-03 17:18:03 |
 Szeretnélek bennetek megkérni arra, ha tudtok valami jó web-címet, amin találhatok összefüggő (hosszú) szöveget az affi-geometriáról, küldjétek el légyszi az e-mail címemre: nytuki@orangeportal.sk. Ha valami jó könyvet is tudtok ajánlani, azt is megköszönném. Köszi
|
|
|
|
| [426] Csimby | 2006-05-08 23:32:51 |
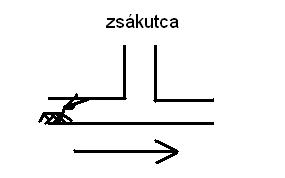
 Vagy inkább annyiféleképpen, ahányféle sorrendben n-2 db. hangya ki tud jönni egy járatból, ha a járat közepén található egy zsákutca (amiben tetszőlegesen sok hangya elfér de nem fér el egyszerre kettő menetiránnyal szemben) :-)
(Mind az n-2 db. hangyának ki kell jönni)
|
 |
| Előzmény: [425] jonas, 2006-05-08 23:05:06 |
|
| [425] jonas | 2006-05-08 23:05:06 |
 Hát igen, ehhez készült az ábra eredetileg.
Ugyanannyiféleképpen, mint ahány n-2 darab egyesből és n-2 darab mínusz egyesből álló sorozat van, aminek minden részletösszege pozitív. A bizonyítás levezethető az eredeti ábra postscript forrásából.
Ezzel, remélem, még nem árulok el sokat.
Elmondom majd a bizonyítást, ha érdekel valakit.
|
| Előzmény: [423] Csimby, 2006-05-08 21:49:32 |
|
|
| [423] Csimby | 2006-05-08 21:49:32 |
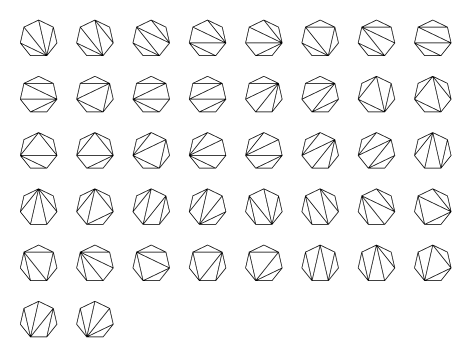
 75. feladat Egy szabályos n-szöget átlóival n-2 db. háromszögre daraboltunk. Hányféleképpen tehetjük ezt meg?
|
|
| [422] jonas | 2006-05-08 21:15:22 |
 Lehet, hogy sokan ismerik a következő feladatot.
73. feladat. Ha egy 2n+1 oldalú szabályos sokszöget 2n-2 átlóval háromszögekre bontunk, akkor milyen határok között változhat a keletkező háromszögek közül a hegyesszögűek száma?
Segítségül itt egy ábra.
|
 |
|
| [421] Vonka Vilmos Úr | 2006-05-02 09:43:54 |
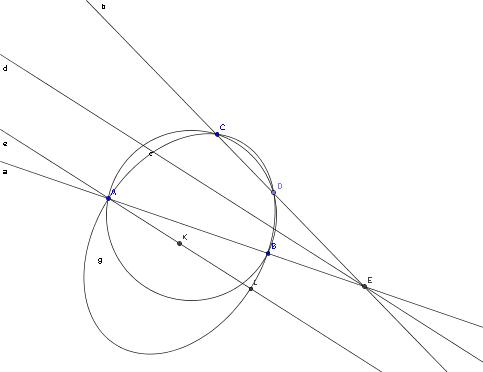
 Ez egy érdekes probléma. Nekem az a gyanúm, hogy ezen a projektív geometria nem tud segíteni. Ha ugyanis megadjuk pl az A, B, C, D pontokat, akkor ahogy kísérletezgettem GeoGebrában, úgy látom, előfordulhat, hogy akár 3 olyan ellipszis is van, aminek ezek pontjai, és A valamelyik tengely végpontja. Ha pedig 3 vagy több megoldás van, akkor hiába is keresünk jó szerkesztési eljárást. Persze az, hogy A a nagytengely, és nem a kistengely végpontja, az egy további szűkítés - ezt azonban projektív módon megfogni nehézkes, legfeljebb úgy tudom elképzelni, hogy valahogyan azt próbáljuk meg kihasználni, hogy a valós fókuszok egyenesén van rajta. Nekem ez sajnos nem sikerült.
Érdekes azonban, hogy ha A, B, C, D egy körön van, akkor már létezik nagyon egyszerű szerkesztési eljárás a tengelyek irányára: projektív eszközökkel ugyanis meg lehet mutatni, hogy akkor az AB, CD egyenesek szögfelezői párhuzamosak lesznek a keresett ellipszis tengelyeivel.
|
 |
| Előzmény: [418] Morci, 2006-04-26 12:00:31 |
|
| [420] Vonka Vilmos Úr | 2006-05-02 09:34:08 |
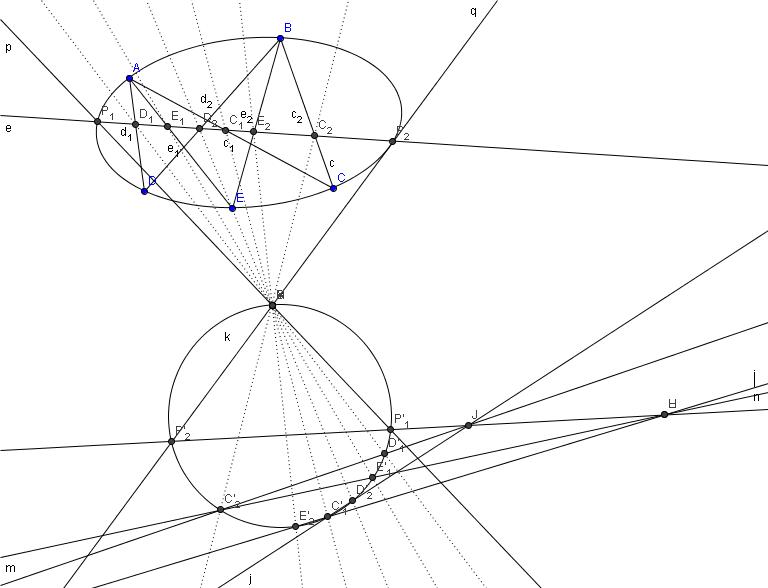
 Ha az ellipszis 5 pontját ismerjük, akkor projektív módon projektív sugársorok metszési alakzataként tudjuk előállítani. A sugársorok közötti projektív leképezést három megfelelő elempár határozza meg, így ha kiválasztjuk az adott A és B pontokat, mint tartópontokat, akkor az AC, AD, AE egyeneseknek megfelelő BC, BD, BE egyenesekkel megadtunk egy, a kúpszeletet meghatározó projektivitást. Ha a sugársorokat metszük az adott (e) egyenessel, akkor az e egyenesen projektív pontosorokat kapunk. Ebben a projektivitásban az önmagának megfelelő pont adja az egyenes és a kúpszelet metszéspontját. Így erre a projektivitásra a Steiner-féle kettőselem-szerkesztést alkalmazva kapjuk meg a keresett metszéspontokat. A Steiner-féle kettőselem-szerkesztésnél a síkon felvett tetszőleges körre annak egy tetszőleges pontjából rávetítjük a projektivitás megfelelő pontpárjait. Kiválasztva (az ábrán például) a C1' és C2' pontokat, rendre a C2', D2', E3' és C1', D1', E1' pontokat vetítve belőlük, perspektív sugársorokat kapunk. Ezen perspektivitás tengelye a kört a P1', P2' pontokban metszi, ezeket visszavetítve az (e) egyenesre, megkapjuk a keresett kettőspontokat.
|
 |
| Előzmény: [419] HoA, 2006-05-02 08:55:07 |
|
|
| [418] Morci | 2006-04-26 12:00:31 |
 Köszönöm a segítséget.
Átgondolom, kipróbálom, lehet lesz még kérdésem... nem ismerem mindegyik dolgot amit leírt, de rákeresgetek. (Nem matematikával-geometriával foglalkozom alapvetően.)
A probléma abban módosult, hogy kiderült nem 5 pont, hanem négy pont alapján kellene előállítani az ellipszist. A pontok közül 1 db az speciális azaz a nagytengely egyik végpontja. a többi 3 darab teljesen általános. Ebben kérnék segítséget. Próbáltam már kérdezgetni több felé, elvileg ez csak számítással oldható meg?
Üdv. Morci
|
| Előzmény: [407] Vonka Vilmos Úr, 2006-04-07 11:25:57 |
|
|
| [416] kenez | 2006-04-16 00:46:57 |
 Az informatikus kollégáktól kérnék segítséget. A probléma a következő. Van egy kockám, és szeretném azt megforgatni egy programmal. 1. kérdés : hogyan számítom ki a 8 csúcspont koordinátáit, ha elforgatom őket x,y,z tengely körül, és mi ennek a matematikai alapja(csak hogy értsem is hogy megy!), 2. kérdés : 3D - 2D leképezés módszere érdekelne nagyon részletesen. Ja és még valami. Van még ingyen letölthető szerkesztőprogi az Euklidesen kívül? Köszi mindenkinek! Kenéz
|
|
| [415] kenez | 2006-04-16 00:20:28 |
 Kösz, HoA, látod, néha még egy mondat is csodákra képes.... A helyzet az, hogy ebbe valóban nem gondoltam bele, mivel a szerkesztésnél annyira evidens volt, és látható, hogy nem gondoltam, hogy bizonyítani kéne. Mivel látványos volt a dolog, abba se gondoltam bele, csak akkor lehet trapéz, ha van egy párhuzamos oldalpárja. Hát nincs is neki. Ennyit erről. Kicsit jobban figyelni(Ezt magamnak mondom!).
|
|
| [414] HoA | 2006-04-15 22:45:14 |
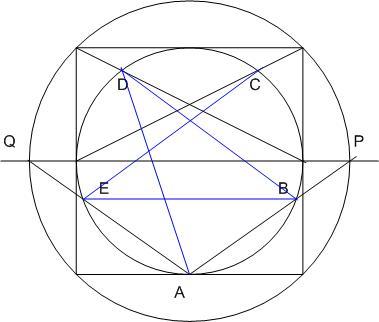
 Ábra (igaz, fejjel lefelé) mellékelve. Segítség: Miből gondolod, hogy pl. ABED húrtrapéz? AE és BD párhuzamosságát bizonyítani kellene.
|
 |
| Előzmény: [412] kenez, 2006-04-15 18:20:50 |
|
| [413] kenez | 2006-04-15 18:27:05 |
 Az ábrát elfelejtettem feltenni!
|
|
| [412] kenez | 2006-04-15 18:20:50 |
 Hello mindenkinek! Megoldottam egy feladatot, mindjárt le is írom a szövegét, a megoldásom viszont nem volt jó, nagyon szeretném, ha valaki megcáfolná az én megoldásomat, megmondaná, miért nem helyes. Köszönettel: Kenéz A feladat: Középkori építészek használták a következő szerkesztést a szabályos ötszög előállítására: Rajzoltak egy négyzetet, aztán megrajzolták a négyzet oldalaival párhuzamos szimmetriatengelyeket, majd a négyzet bele- és köréírt körét. A négyzet A oldalfelező pontját összekötötték a körülírt kör PQ átmérőjének végpontjaival. A négyzet beírt körét az AP és PQ szakaszok a B és E pontokban, a négyzet alsó felét adó KLMN téglalap átlói pedig a C és a D pontokban metszik. Az ABCDE pontok alkotják az ötszöget. Valóban szabályos ez az ötszög?
Az én megoldásom: Behúzva az AD BE CE BD szakaszokat, húrtrapézokat kapunk. Az ABED húrtrapézból : AB = ED. CEAB húrtrapézból : CB = AE. DABC húrtrapézból : AB = CD Eddig : AB = ED = CD EBCD húrtrapézból : CB = ED Tehát : AB = ED = CD = CB = AE Tehát ez egy olyan ötszög, amelynek minden oldala egyenlő, vagyis szabályos. Hol van a hiba a logikámban?
|
|
| [411] HoA | 2006-04-15 15:52:08 |
 [409] után a 68. - 70. - 71. feladatok tkp. a [388] -ban felvetett egyenlőtlenség szemléletes bizonyításai. Adjuk fel 72. feladat-ként az egyenlőtlenség trigonometriai - ábrát nem igénylő - bizonyítását.
Érdekességképpen megemlítem, hogy a tételre a Matematikai Versenytételek 1897(!!)-i egyik feladataként is rátaláltam. Igaz, ott az állítás nem ilyen éles, csak a
sin( /2) * sin( /2) * sin( /2) * sin( /2) * sin( /2) /2)  1/4 1/4
igazolását tűzték ki. A megoldás 1/8 -ra is szerepel.
|
| Előzmény: [409] BohnerGéza, 2006-04-12 00:44:01 |
|














 /2) * sin(
/2) * sin( /2) * sin(
/2) * sin( /2)
/2)  1/4
1/4