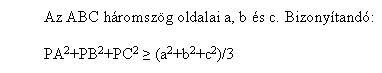|
| [611] lorantfy | 2007-01-27 11:14:46 |
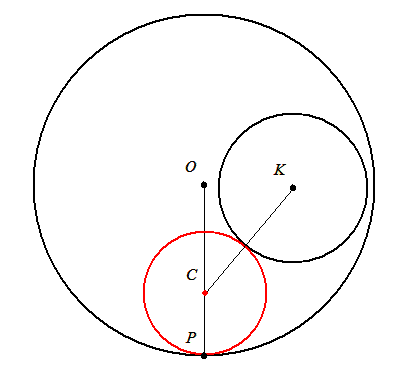
 102. feladat: Adott az O középpontú R sugarú kör és belsejében az O-tól különböző, K középpontú r sugarú kör. Szerkesszönk olyan kört, mely a nagy kört egy adott P pontban érinti és érinti a kisebb kört is!
|
 |
|
| [610] BohnerGéza | 2007-01-25 12:11:02 |
 101. feladat: ( Megpróbálom, hátha sikerül sorszámozni a további feladatokat. )
|
 |
|
|
| [608] epsilon | 2007-01-11 11:49:45 |
 Köszi, megnéztem, hát onnan látszik a feladat "fajsúlya" ;-)
|
|
|
| [606] epsilon | 2007-01-11 11:14:12 |
 Hmmmm....hát kellett nekem :-) valóban implicit, mégis valamivel barátságosabbra gondolta, ez is a körszeletekből származik? Mert Én úgy próbáltam, hogy 2 szembennálló körszelet összegeként fogtam fel, a 2 körben, ott egzenlőre a sugár ami ismeretlen, meg 2 középponti szög, persze lehet kifejezni...de gyökös összefüggések lettek :-( Ha jó hallottam, ezt a feladatot valamikor a Danubiusz rádióban adták fel, és azt szeretném megtudni, hogy vajon milyen megoldást vártak volna el, pontosabban milyen eredményt, a helyes megoldásként...vagy csak szívatás volt?
|
|
|
|
| [603] epsilon | 2007-01-11 10:15:43 |
 Helló Cckek! Az igazolása affixumokkal csak algebrai számolás. Az illető csúcs megfelelő kisbetűjével jelölve az illető affixumot, a bizonyítandó összefüggés: 4(o1-h)+ 4(o2-h)+ 4(o3-h)= 15(g-h) vagyis 4(o1+o2+o3)=15g-3h és legyen a köréírt kör középpontja éppen az O origó, ekkor g=(a+b+c)/3 és h=a+b+c, és így elegendő bizonyítani, hogy: 2(o1+o2+o3)=a+b+c (*). Az előző indoklás alapján PO vektor=2 RO1 vektor (a az indoklást lásd előbb) és ezt affixumokkal felírva 0-p=2(o1-r)továbbá p=(b+c)/2, r=(m+n)/2 és az m, n a felezőpontokra vonatkozó affixumokat is használva, o1=a/2 adódik és analógjai (ezt még másképpen is bizonyíthatjuk) és a (*) összefüggés így valóban teljesül. (a bizonyítandó kép a hszm alján van!)
|
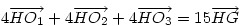 |
| Előzmény: [593] HoA, 2007-01-08 15:59:17 |
|
|
| [601] epsilon | 2007-01-10 22:07:38 |
 Kösz a megjegyzést, valóban ott van, most olvastam az ott leírt megjegyzéseket, ...de nem bíztatóak, valamilyen kifejezést szeretnék találni az R függvényében (nem megközelítő megoldást)de a körszeletekkel elindulva, két körszeletből összerakva egyenlőre semmi bíztató nem jött ki (még maradt kiküszöböletlen paraméter is :-(
|
|
| [600] psbalint | 2007-01-10 21:44:42 |
 azt hiszem éppen erről a feladatról volt szó az Érdekes matekfeladatok topikban
|
|
| [599] epsilon | 2007-01-10 20:48:52 |
 Helló! BÚÉK Mindenkinek! Létezik-e elemi megoldás a következő, ismertnek tűnő feladatra: Adott egy 1 egységsugarú körlap. Annak kerületén vegyünk fel egy tetszőleges M pontot, és az M középponttal, R sugárral rajzoljunk egy körívet, ami az adott körlapot két kükönböző pontban metszi. Mekkora kell legyen az R, hogy a "közrezárt" síkrész területe az 1 sugarú kör területének a fele legyen? Előre is kösz az esetleges támpontokat! Üdv: epsilon
|
|
| [598] HoA | 2007-01-10 15:51:57 |
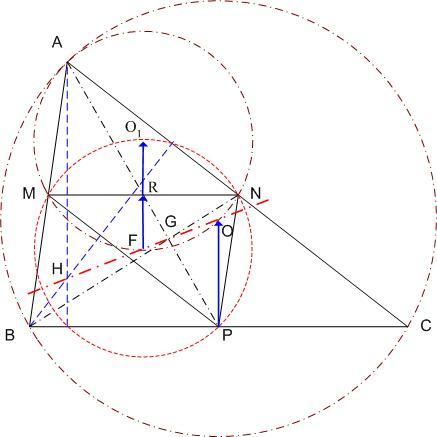
 A bizonyítás, ahol egy 3-as szorzóval elszámoltam magamat :-) : Cckek jelöléseivel ( ha már... ), legyen a körülírt kör középpontja O, a Feuerbach köré F, MN felezőpontja R. ABC  az AMN az AMN  A-ból vett kétszeres nagyítása, így A-ból vett kétszeres nagyítása, így 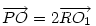 . AMN . AMN  és PNM és PNM  egymás tükörképei R-re, ezért egymás tükörképei R-re, ezért 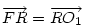 , vagyis , vagyis 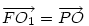 . .
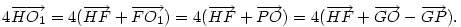 Hasonlóan Hasonlóan 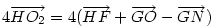 és és 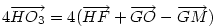 A hármat összeadva A hármat összeadva 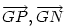 és és 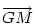 kiesik, mert egy kiesik, mert egy  súlyvonalainak harmadai, így vektorösszegük súlyvonalainak harmadai, így vektorösszegük  . Igazolandó : . Igazolandó : 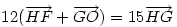 . Legyen az Euler-egyenesen . Legyen az Euler-egyenesen 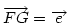 . Ekkor . Ekkor 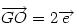 , ,  és és 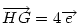 . Egyenlőségünk tehát . Egyenlőségünk tehát 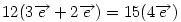 , amit már nem nehéz belátni. , amit már nem nehéz belátni.
|
 |
| Előzmény: [595] HoA, 2007-01-09 11:13:46 |
|
|
|
|
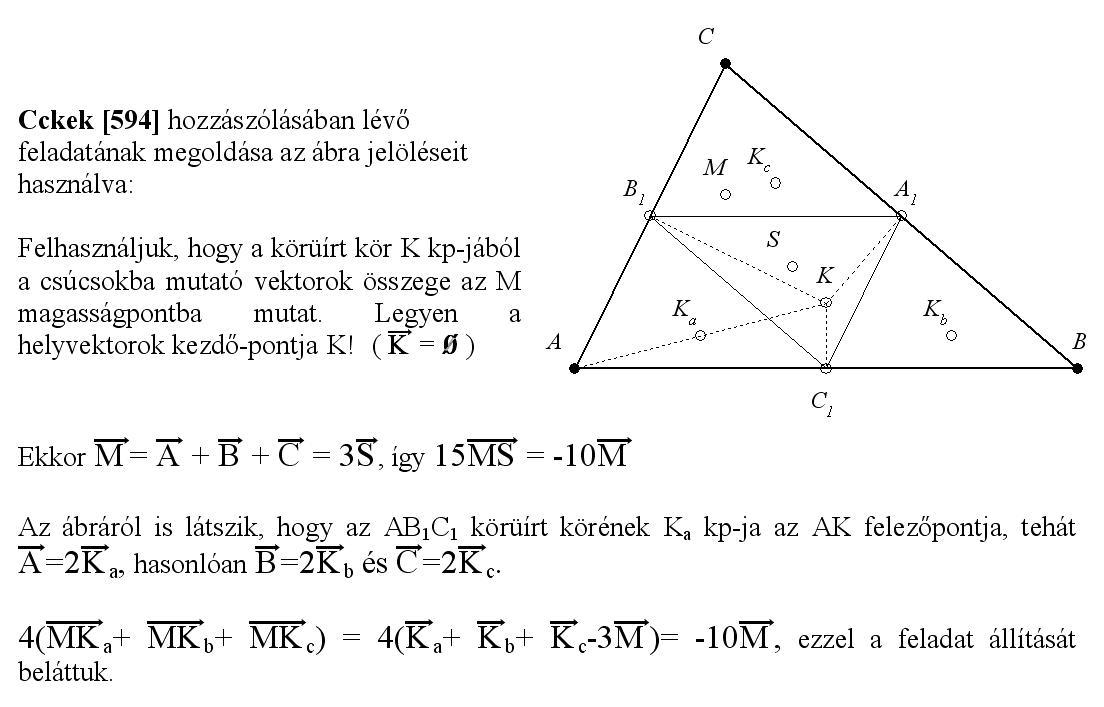
| [594] Cckek | 2007-01-08 21:12:11 |
 Legyen G az ABC háromszög súlypontja, H az ortocentruma, M, N, P az AB, AC, BC oldalak felezőpontjai, O1,O2,O3 az AMN, BMP illetve CNP háromszögek köré írt körök középpontjai. Bizonyítsuk be hogy : 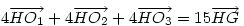
|
|
| [593] HoA | 2007-01-08 15:59:17 |
 Mivel két hete senki sem szólt hozzá, leírok egy megoldást. Nézzük meg, mi a mértani helye a síkban azoknak a pontoknak, melyekre az ABC  csúcsaitól mért távolságok négyzetösszege csúcsaitól mért távolságok négyzetösszege
adott konstans?
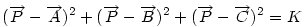
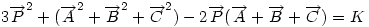 Ha origónak az ABC Ha origónak az ABC  S súlypontját választjuk, S súlypontját választjuk, 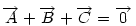 ; ;  , ami adataink által meghatározott konstans. A mértani hely tehát egy S középpontú kör, a sugár négyzete a jobboldali kifejezés, ami akkor nemnegatív, ha , ami adataink által meghatározott konstans. A mértani hely tehát egy S középpontú kör, a sugár négyzete a jobboldali kifejezés, ami akkor nemnegatív, ha 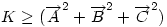 (1) baloldala tehát akkor a legkisebb, ha P a súlypont, értéke ekkor (1) baloldala tehát akkor a legkisebb, ha P a súlypont, értéke ekkor 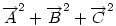 . Most már csak azt kell igazolni, hogy ez megegyezik a háromszög oldalai négyzetösszegének harmadával. De . Most már csak azt kell igazolni, hogy ez megegyezik a háromszög oldalai négyzetösszegének harmadával. De 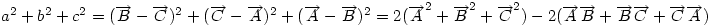 Origó választásunk miatt Origó választásunk miatt 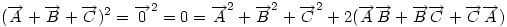 Innen Innen 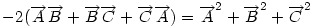 Tehát valóban Tehát valóban 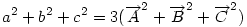
|
| Előzmény: [588] BohnerGéza, 2006-12-25 22:50:17 |
|
| [592] Sirpi | 2007-01-05 16:10:42 |
 Ezt hívják Euler-egyenesnek, és ráadásul az S pont harmadolja (O-hoz közelebb) az OM szakaszt.
Egybe akkor és csak akkor esnek, ha a háromszög szabályos.
|
| Előzmény: [591] Cckek, 2007-01-05 16:04:29 |
|
| [591] Cckek | 2007-01-05 16:04:29 |
 Igaz-e, hogy bármely háromszögben az ortocentrum, a súlypont és a háromszög köré írt kör középpontja kollineárisak? (vagy egybeesnek:)
|
|
|
| [589] HoA | 2006-12-27 10:11:54 |
 BohnerGéza ábrája alapján ha az  , , , , paraméterekkel kifejezett koordinátákra felírjuk az paraméterekkel kifejezett koordinátákra felírjuk az 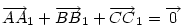 vektoregyenletet, rövid számolás után kapjuk, hogy vektoregyenletet, rövid számolás után kapjuk, hogy  = = = = , vagyis P (Cckek-nél M) = , vagyis P (Cckek-nél M) = 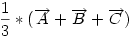 , vagyis M a súlypont. , vagyis M a súlypont.
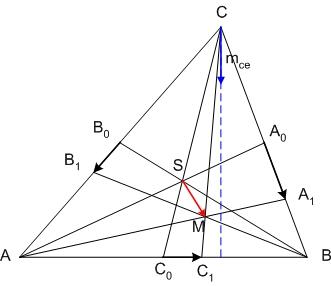
Ha [582] "akkor" ágának bizonyítására elfogadjuk az [586] ábráját, a "csak akkor" ágra itt egy - talán kicsit szemléletesebb - bizonyítás. Legyenek a háromszög oldalfelező pontjai A0,B0,C0 , a súlypont S, továbbá M, A1,B1,C1 [582] szerint. A súlyvonalak a háromszöget hat kis háromszögre osztják. Az általánosság megszorítása nélkül feltehetjük, hogy M a C0BS háromszög belsejében vagy határán van. Mivel pl. 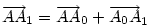 és tudjuk, hogy és tudjuk, hogy 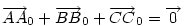 , , 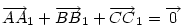 pontosan akkor teljesül, ha pontosan akkor teljesül, ha
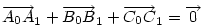 | (1) |
. Ha a három vektor összege 0, akkor tetszőleges irányú vetületüké is az. Tekintsük az mc magasságra vett vetületeket - az mce egységvektorral vett skaláris szorzatokat. Ez 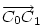 esetében nyilván 0. M választása miatt A1 nincs messzebb B-től, mint A0 és B1 nincs messzebb A-tól, mint B0 . Így esetében nyilván 0. M választása miatt A1 nincs messzebb B-től, mint A0 és B1 nincs messzebb A-tól, mint B0 . Így 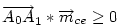 és és 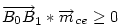 . Ezért (1) csak úgy teljesülhet, ha A0=A1 és B0=B1 , vagyis M=S. . Ezért (1) csak úgy teljesülhet, ha A0=A1 és B0=B1 , vagyis M=S.
|
 |
| Előzmény: [587] BohnerGéza, 2006-12-25 22:49:35 |
|
|








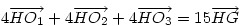


 az AMN
az AMN 

 ,
, ,
, paraméterekkel kifejezett koordinátákra felírjuk az
paraméterekkel kifejezett koordinátákra felírjuk az