|
| [636] BohnerGéza | 2007-02-12 22:00:07 |
 Egy aktuális, de egyáltalán nem közismert feladat:
B. 3970. Bizonyítsuk be, hogy egy egységnyi oldalú szabályos hétszög átlói hosszának harmonikus közepe 2.
|
| Előzmény: [632] Doom, 2007-02-11 11:15:38 |
|
| [635] Doom | 2007-02-11 13:35:31 |
 Ilyenekre gondoltam, köszi mindkettőtöknek!
|
|
|
| [633] V Laci | 2007-02-11 12:06:34 |
 Én most hirtelen két geometriai példát tudnék mondani:
1) Trapézban, a átlók metszéspontján át húzott, az alapokkal párhuzamos egyenes trapézon belüli része a két alap harmonikus közepe.
2) Háromszög egyik szögfelezőjére, a szemközti oldallal való metszéspontjából állított merőleges kimetsz egy szakaszt az egyik oldalból. Ez a szakasz a szögfelezővel szomszédos két oldal harmonikus közepe.
Ilyen "geometriai jelentésre" gondoltál?
|
| Előzmény: [632] Doom, 2007-02-11 11:15:38 |
|
| [632] Doom | 2007-02-11 11:15:38 |
 Nem tudjátok véletlenül, hogy a harmonikus középnek milyen geometriai jelentése van? Előre is kösz!
|
|
|
|
|
| [628] BohnerGéza | 2007-02-06 20:48:35 |
 Nem tudom, hogy képességvizsga feladatnak a 8. osztályosok számára jó-e a feladat. Talán nem. (HoA hozzászólása is ezt erősíti bennem) A lényege általánosabban is használható.
Nem kell, hogy a BAD szög derékszög legyen. Jelöljük ezt a szöget fí-vel, ekkor 180 fok - fí forgatással oldhatjuk meg a feladatot. Ennek speciális esete, ha fí 0 fok ( az e egyenes egy partján van A és B, jussunk el A-ból e-t érintve B-be a legrövidebb úton ).
Gondolkodhatunk így is: Használjunk egy AA'-t tartalmazó síktükröt! Állítsuk úgy, hogy B'-ből lássuk benne D-t! ...
Nehezítek kicsit a feladaton: 104. feladat: Jussunk el minnél rövidebb úton B'-ből AA'-t és DD'-t érintve C-be úgy, hogy AA' és DD' között adott irányt kell követnünk! ( Az irányt az AA'D'D síkkal párhuzamos egyenessel adhatjuk meg. )
|
| Előzmény: [626] Cckek, 2007-02-05 16:29:55 |
|
| [627] HoA | 2007-02-06 12:44:26 |
 Igen, a lényeg az, beugrik-e valakinek a síkba forgatás ötlete. Aki találkozott már a "pók legrövidebb útja a szoba falain a légyig" feladattípussal, annak persze nem nehéz.
|
| Előzmény: [626] Cckek, 2007-02-05 16:29:55 |
|
| [626] Cckek | 2007-02-05 16:29:55 |
 Szép megoldás. Amúgy ez a feladat képességvizsga feladat a 8. osztályosok számára, itt Romániában, és ha nem ismertem volna hasonló módszert nem tudom hogyan lehetett volna 8. osztályos szinten megoldani.
|
| Előzmény: [625] BohnerGéza, 2007-02-05 12:34:31 |
|
|
| [624] Cckek | 2007-02-05 05:20:14 |
 103.feladat Lehet hogy a forumozók elsiklottak a feladat fölött.:) Egy ABCDA'B'C'D' téglatest éleinek a hossza AB=a, BC=b, AA'=c. Legyen Q (AA'). Határozzuk meg a QA értéket, úgy hogy a B'QD háromszög kerülete minimális legyen (AA'). Határozzuk meg a QA értéket, úgy hogy a B'QD háromszög kerülete minimális legyen
|
|
| [623] Cckek | 2007-02-05 05:19:01 |
 102. Lehet hogy a forumozók elsiklottak a feladat fölött.:) Egy ABCDA'B'C'D' téglatest éleinek a hossza AB=a, BC=b, AA'=c. Legyen Q (AA'). Határozzuk meg a QA értéket, úgy hogy a B'QD háromszög kerülete minimális legyen (AA'). Határozzuk meg a QA értéket, úgy hogy a B'QD háromszög kerülete minimális legyen
|
|
| [622] Csimby | 2007-02-02 10:37:26 |
 Köszönöm a sok szép megoldást :-)
|
|
|
|
|
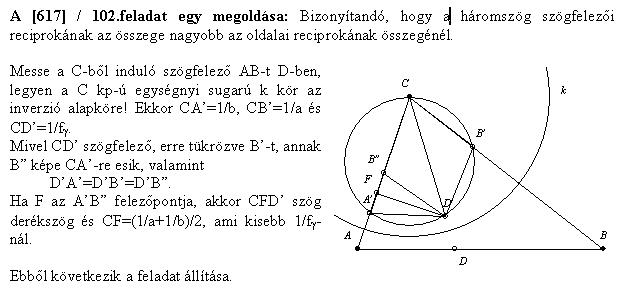
| [618] Cckek | 2007-01-31 22:22:35 |
 Jelölje ia,ib,ic a háromszog szögfelezőit a,b,c az oldalait, írhatjuk:
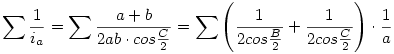 . .
Tehát csak annyit kell bizonyítani, hogy
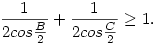 , ,
ami egyenértékű az
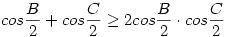 , ,
egyenlőtlenséggel. De a
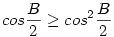
egyenlőtlenség miatt ez utóbbi fennáll.
|
| Előzmény: [617] Csimby, 2007-01-31 21:52:50 |
|
| [617] Csimby | 2007-01-31 21:52:50 |
 102.feladat Igaz-e és ha igen bizonyítsuk be, hogy tetszőleges háromszög szögfelezőinek a reciprokának az összege nagyobb az oldalai reciprokának az összegénél.
|
|
| [616] Cckek | 2007-01-31 21:43:36 |
 Nagyon érdekes feladat, főleg mivel általános iskolai színtű bizonyítást igényel. Egy ABCDA'B'C'D' téglatest éleinek a hossza a,b,c. Legyen Q AA'. Határozzuk meg a QA értéket, úgy hogy a B'QD háromszög kerülete minimális legyen. AA'. Határozzuk meg a QA értéket, úgy hogy a B'QD háromszög kerülete minimális legyen.
|
|
|
| [614] HoA | 2007-01-30 10:46:31 |
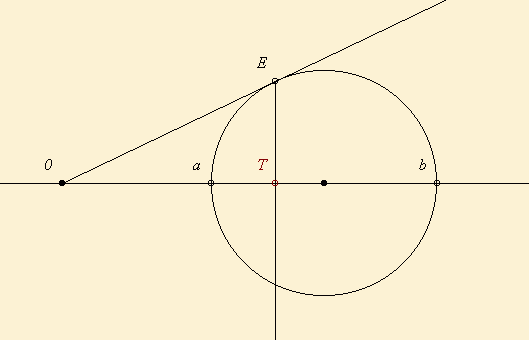
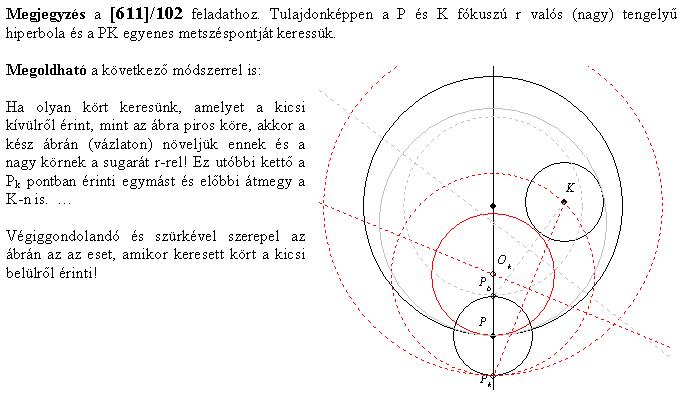
 A feladat a "Geometriai feladatok gyűjteményében" is szerepel. Az ottani megoldás sem bonyolult. Azon alapul, hogy a kis K2 kör és a szerkesztendő K3 kör T érintési pontja K2 és K3 hasonlósági pontja, és mivel C az OP egyenesen van, a hasonlóságban P megfelelője K2-n az OP-vel párhuzamos átmérő valamelyik végpontja (Q1, Q2). PQi kimetszi K2-ből T-t, TK és PO metszéspontja C. A választástól függően a K2-t kívülről illetve belülről érintő K3 kört kapjuk.
|
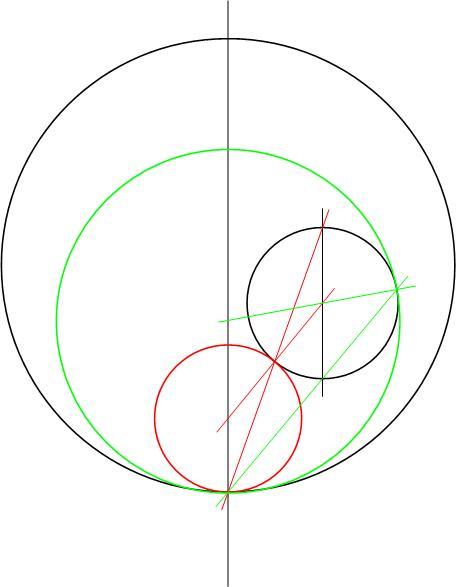 |
| Előzmény: [613] lorantfy, 2007-01-30 09:13:35 |
|
| [613] lorantfy | 2007-01-30 09:13:35 |
 Szia Attila!
Kösz a megolgást! Végülis ilyen egyszerű az egész. Szemléletesebb talán azt mondani, hogy az S pontban vegyünk fel egy r sugarú kört. Így két egyenlő sugarú körhöz kell érintőkört szerkesztenünk, tehát a keresett C pont rajta van a szimmetria tengelyen, vagyis KS felező merőlegesén.
|
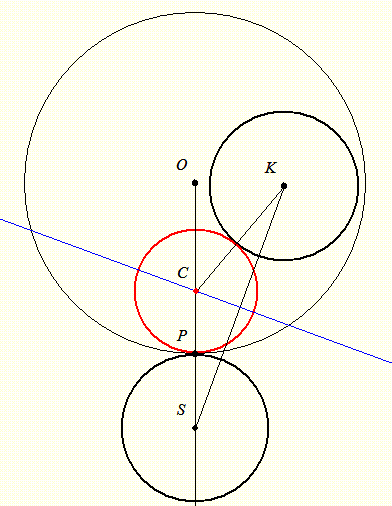 |
| Előzmény: [612] jenei.attila, 2007-01-29 14:01:30 |
|








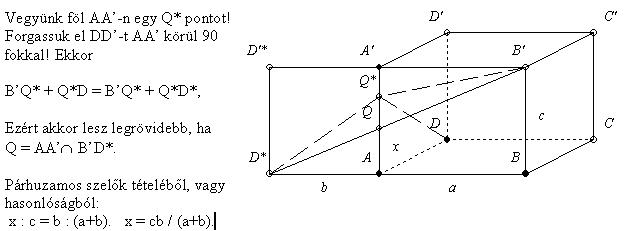
 (AA'). Határozzuk meg a QA értéket, úgy hogy a B'QD háromszög kerülete minimális legyen
(AA'). Határozzuk meg a QA értéket, úgy hogy a B'QD háromszög kerülete minimális legyen
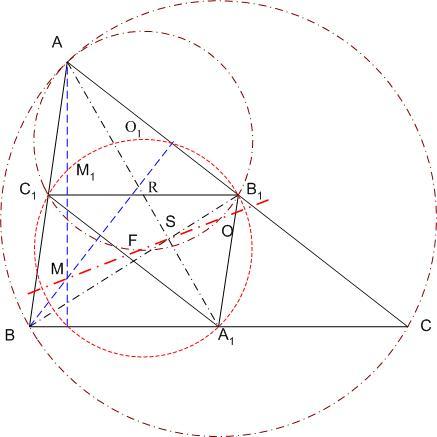
 körülírt köre ABC Feuerbach köre, ezért átmegy az AM szakasz M1 felezőpontján. ABC
körülírt köre ABC Feuerbach köre, ezért átmegy az AM szakasz M1 felezőpontján. ABC