| [646] BohnerGéza | 2007-02-22 11:51:37 |
 A Ptolemaiosz-tétel szerint a négyszög átlói és oldalai közt igaz, hogy e*f <= a*c+b*d, ahol az egyenlőség húrnégyszögben és csak abban igaz.
Az ABCDEFG szabályos hétszög esetén alkalmazzuk a tételt pl. az ACDE négyszögre, ekkor e*f = a*e+a*f ahonnan az állítás következik.
|
| Előzmény: [636] BohnerGéza, 2007-02-12 22:00:07 |
|
| [645] lorantfy | 2007-02-22 08:38:32 |
 Szia Laura!
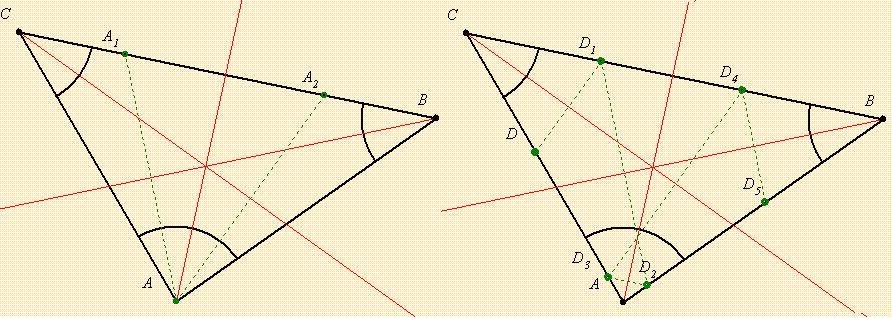
A három szögfelező kevés, kell még egy pont is.
Ha az adott pont mondjuk az A csúcs, akkor tükrözve a másik két szögfelezőre, mindkét pont a BC oldalra esik.Ezt meghúzva megvan B és C.
Ha egy D kerületi pont van megadva, akkor sorra tükrözzük a három szögfelezőre, addig, míg minden oldalon 2-2 pontot kapunk.
|
 |
| Előzmény: [644] lauraa, 2007-02-21 19:07:11 |
|
| [644] lauraa | 2007-02-21 19:07:11 |
 sziasztok! nem tudja valaki, hogyan lehet megszerkeszteni egy 3szöget, ha adott 3 szögfelezője? köszi előre :-)
|
|
| [643] HoA | 2007-02-21 00:48:30 |
 Egy megoldás [619] mintájára: A szabályos hétszögnek 7 rövidebb és 7 hosszabb átlója van, ezek harmonikus közepe megegyezik egy rövidebb és egy hosszabb átló harmonikus közepével. Tekintsük az egységnyi oldalú ABCDEFG szabályos hétszög AC és AD átlóját. Azt kell igazolni, hogy 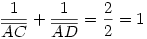 Legyen a hétszög körülírt köre k1, az inverzió k2 alapkörének középpontja A, sugara Legyen a hétszög körülírt köre k1, az inverzió k2 alapkörének középpontja A, sugara 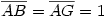 . Mivel k1 átmegy A-n, inverze a BG egyenes, így C és D C' ill. D' képe is ide esik. Legyen AD és k2 metszéspontja H. . Mivel k1 átmegy A-n, inverze a BG egyenes, így C és D C' ill. D' képe is ide esik. Legyen AD és k2 metszéspontja H. 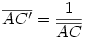 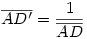 . Bizonyítandó: . Bizonyítandó: 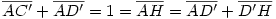 , vagyis elég megmutatni, hogy , vagyis elég megmutatni, hogy 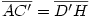 . Az ábrán zölddel jelölt ABG, BAC és CAD szögek . Az ábrán zölddel jelölt ABG, BAC és CAD szögek 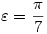 nagyságúak, mert egy szabályos hétszög körülírt körében az oldalakhoz tartozó kerületi szögek. ABC' nagyságúak, mert egy szabályos hétszög körülírt körében az oldalakhoz tartozó kerületi szögek. ABC'  egyenlőszárú, egyenlőszárú, 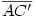 = = 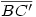 . AC a BAH középponti szög felezője, így BH felező merőlegese, . AC a BAH középponti szög felezője, így BH felező merőlegese, 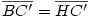 . AC'H . AC'H  egyenlőszárú, AHC' szög = egyenlőszárú, AHC' szög =  . C'D'H . C'D'H  = AD'G = AD'G  = 3 = 3 mint az ABD' mint az ABD'  külső szöge. De ekkor a HC'D' külső szöge. De ekkor a HC'D'  -ben a HC'D' -ben a HC'D'  = = -4. -4. =3. =3. , HC'D' , HC'D'  egyenlőszárú, egyenlőszárú, 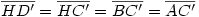 , amit igazolni akartunk. , amit igazolni akartunk.
|
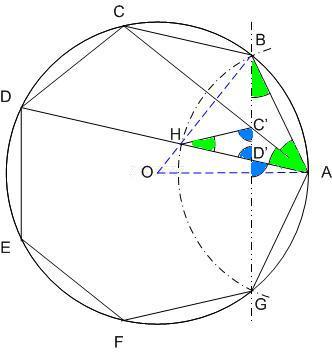 |
| Előzmény: [636] BohnerGéza, 2007-02-12 22:00:07 |
|
| [642] nadorp | 2007-02-19 08:51:18 |
 Ha a szabályos 14-szöget egységnyi sugarú körbe írjuk, akkor nyilván elég belátni, hogy A0A1.A0A3.A0A5=1. Legyen x az első 14-dik komplex egységgyök. ( nem akarok  -t írni, mert akkor túl sokat kéne gépelni -:). Ekkor x7=-1 miatt -t írni, mert akkor túl sokat kéne gépelni -:). Ekkor x7=-1 miatt
A=A0A1.A0A3.A0A5=|x-1||x3-1||x5-1|=|(x-1)(x8-x3-x5+1)|=(x-1)(-x-x3-x5+1)|
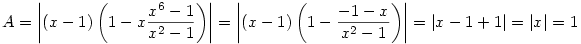
|
| Előzmény: [639] BohnerGéza, 2007-02-18 00:54:57 |
|
|
|
|
| [638] fermel | 2007-02-17 14:42:37 |
 Egy kombinatorikai feladat megoldásában szeretném a segítségeteket kérni. Azért ide írom, mert a probléma végül is geometriai. Adott egy 3x4-es téglalap. Bizonyítsuk be, hogy bárhogyan is adunk meg benne 6 pontot, biztos, hogy található köztük kettő, melyek távolsága nem nagyobb , mint négyzetgyök 5! A feladat 7 pont esetén nagyon egyszerű. Felosztjuk a téglalapot 6 db 2x1-es téglalapra. Ez 6 skatulya. 7 pont közül biztosan van legalább kettő, amelyik ugyanabba a skatulyába tartozik, azon belül pedig a maximális távolság valóban négyzetgyök 5. Megfelelő skatulyák megválasztásával már 6 pontra is igaz. Sajnos nem találom az 5 részre való felosztás módját. Köszönöm a segítséget. (Elnézést a négyzetgyök 5 kezdetleges írásmódjától, de hiába írtam be Worldben jól, nem másolta át nekem ide.)
fermel
|
|
|
| [636] BohnerGéza | 2007-02-12 22:00:07 |
 Egy aktuális, de egyáltalán nem közismert feladat:
B. 3970. Bizonyítsuk be, hogy egy egységnyi oldalú szabályos hétszög átlói hosszának harmonikus közepe 2.
|
| Előzmény: [632] Doom, 2007-02-11 11:15:38 |
|
| [635] Doom | 2007-02-11 13:35:31 |
 Ilyenekre gondoltam, köszi mindkettőtöknek!
|
|
|
| [633] V Laci | 2007-02-11 12:06:34 |
 Én most hirtelen két geometriai példát tudnék mondani:
1) Trapézban, a átlók metszéspontján át húzott, az alapokkal párhuzamos egyenes trapézon belüli része a két alap harmonikus közepe.
2) Háromszög egyik szögfelezőjére, a szemközti oldallal való metszéspontjából állított merőleges kimetsz egy szakaszt az egyik oldalból. Ez a szakasz a szögfelezővel szomszédos két oldal harmonikus közepe.
Ilyen "geometriai jelentésre" gondoltál?
|
| Előzmény: [632] Doom, 2007-02-11 11:15:38 |
|
| [632] Doom | 2007-02-11 11:15:38 |
 Nem tudjátok véletlenül, hogy a harmonikus középnek milyen geometriai jelentése van? Előre is kösz!
|
|
|
|
|
| [628] BohnerGéza | 2007-02-06 20:48:35 |
 Nem tudom, hogy képességvizsga feladatnak a 8. osztályosok számára jó-e a feladat. Talán nem. (HoA hozzászólása is ezt erősíti bennem) A lényege általánosabban is használható.
Nem kell, hogy a BAD szög derékszög legyen. Jelöljük ezt a szöget fí-vel, ekkor 180 fok - fí forgatással oldhatjuk meg a feladatot. Ennek speciális esete, ha fí 0 fok ( az e egyenes egy partján van A és B, jussunk el A-ból e-t érintve B-be a legrövidebb úton ).
Gondolkodhatunk így is: Használjunk egy AA'-t tartalmazó síktükröt! Állítsuk úgy, hogy B'-ből lássuk benne D-t! ...
Nehezítek kicsit a feladaton: 104. feladat: Jussunk el minnél rövidebb úton B'-ből AA'-t és DD'-t érintve C-be úgy, hogy AA' és DD' között adott irányt kell követnünk! ( Az irányt az AA'D'D síkkal párhuzamos egyenessel adhatjuk meg. )
|
| Előzmény: [626] Cckek, 2007-02-05 16:29:55 |
|
| [627] HoA | 2007-02-06 12:44:26 |
 Igen, a lényeg az, beugrik-e valakinek a síkba forgatás ötlete. Aki találkozott már a "pók legrövidebb útja a szoba falain a légyig" feladattípussal, annak persze nem nehéz.
|
| Előzmény: [626] Cckek, 2007-02-05 16:29:55 |
|
| [626] Cckek | 2007-02-05 16:29:55 |
 Szép megoldás. Amúgy ez a feladat képességvizsga feladat a 8. osztályosok számára, itt Romániában, és ha nem ismertem volna hasonló módszert nem tudom hogyan lehetett volna 8. osztályos szinten megoldani.
|
| Előzmény: [625] BohnerGéza, 2007-02-05 12:34:31 |
|
|
| [624] Cckek | 2007-02-05 05:20:14 |
 103.feladat Lehet hogy a forumozók elsiklottak a feladat fölött.:) Egy ABCDA'B'C'D' téglatest éleinek a hossza AB=a, BC=b, AA'=c. Legyen Q (AA'). Határozzuk meg a QA értéket, úgy hogy a B'QD háromszög kerülete minimális legyen (AA'). Határozzuk meg a QA értéket, úgy hogy a B'QD háromszög kerülete minimális legyen
|
|
| [623] Cckek | 2007-02-05 05:19:01 |
 102. Lehet hogy a forumozók elsiklottak a feladat fölött.:) Egy ABCDA'B'C'D' téglatest éleinek a hossza AB=a, BC=b, AA'=c. Legyen Q (AA'). Határozzuk meg a QA értéket, úgy hogy a B'QD háromszög kerülete minimális legyen (AA'). Határozzuk meg a QA értéket, úgy hogy a B'QD háromszög kerülete minimális legyen
|
|
| [622] Csimby | 2007-02-02 10:37:26 |
 Köszönöm a sok szép megoldást :-)
|
|







 egyenlőszárú,
egyenlőszárú,  . C'D'H
. C'D'H  = AD'G
= AD'G  -4.
-4.
 -t írni, mert akkor túl sokat kéne gépelni -:). Ekkor x7=-1 miatt
-t írni, mert akkor túl sokat kéne gépelni -:). Ekkor x7=-1 miatt 

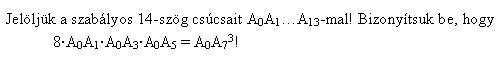



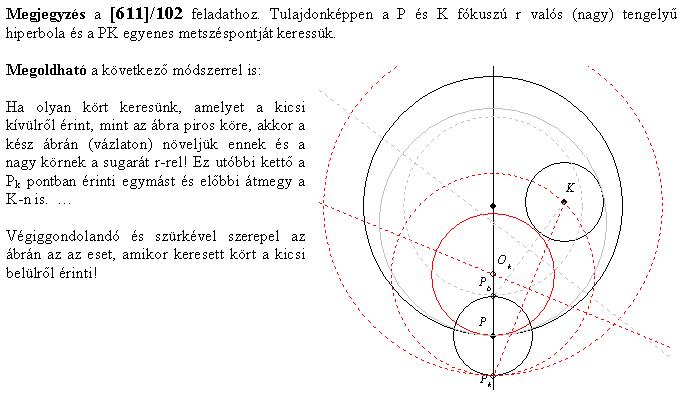

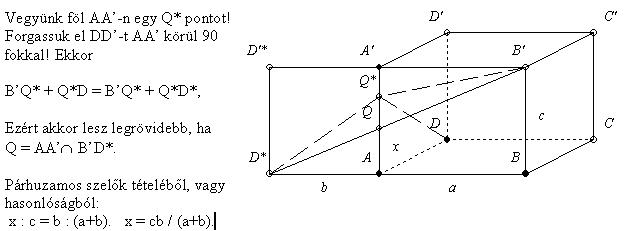
 (AA'). Határozzuk meg a QA értéket, úgy hogy a B'QD háromszög kerülete minimális legyen
(AA'). Határozzuk meg a QA értéket, úgy hogy a B'QD háromszög kerülete minimális legyen