|
| [686] epsilon | 2007-03-25 07:56:00 |
 Helló! Köszi mindannyiatoknak! A feladatot azért kezelem gyanakvóan, mert tudjuk, láttuk, hogy indukcióval olyasmit is lehet bizonyítani, ami nem igaz (pl 2 egymásutáni szám egyenlő, ha ezt igaznak feltételezzük, a következő lépés is kijön), tehát az bizonytalan, hogy a legfennebb n(n+1)/2 +1 felső korlát el is érhető, minden n-re? Üdv: epsilon
|
|
|
| [684] V Laci | 2007-03-24 21:52:41 |
 Szia.
Legfeljebb 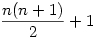 részre osztja a síkot n db egyenes. Ezt teljes indukcióval láthatod be: az n. egyenes behúzása legfeljebb n+1 új síkrészt eredményezhet. részre osztja a síkot n db egyenes. Ezt teljes indukcióval láthatod be: az n. egyenes behúzása legfeljebb n+1 új síkrészt eredményezhet.
|
| Előzmény: [682] epsilon, 2007-03-24 21:33:09 |
|
| [683] Sirpi | 2007-03-24 21:51:16 |
 0 egyenes 1 részre, 1 egyenes 2 részre, majd a k. egyenes mind a korábbi k-1-et metszve k db. új részt hoz létre, így a válasz:
1+(1+2+...+n)=n(n+1)/2+1
|
| Előzmény: [682] epsilon, 2007-03-24 21:33:09 |
|
| [682] epsilon | 2007-03-24 21:33:09 |
 Heló! Tudna-e Valaki segíteni ebben a kérdésben: legtöbb hány részre osztja a síkor "n" darab egyenes? Előre is kösz! Üdv: epsilon
|
|
|
|
|
| [678] HoA | 2007-03-14 16:54:19 |
 Idézet következik Szénássy Barna korabeli magyar nyelven megírt írásából, melynek címe: Jelentés a császári és királyi inspektornak az helvét vallású kollégyum tiszta tudákosság leckéin végzett vizitációjáról.
"Hanem aztán az harmadik deák-klasszisban baj is lőn. Mikoron ugyanis junior Gyarmati praeceptor uram az lap-háromszögelléseket oktatván megkérdezé Toldallagi földmérő Ábris nevű fatytyát, mi jutna eszébe hallván eztet: kebel x, az deák válaszolá, neki bizon nyugalmazott enzsenőr kapitán Bolyai János szépséges Szöts Júlia nevezetű szolgáló-leána. Továbbiglan az praeceptor uram meg sem kérdezé az pótkebelt, az visszáskebelt és az visszás-pótkebelt." (Staar 1990: 129)
Nyilvánvaló, hogy egy matematikai fogalom megnevezésére a kebel szó nem a legalkalmasabb, hiszen ez a diákokban, elsősorban a fiúkban, más jellegű asszociációkat ébreszt. A kebel egyébként a hasonló jelentésű latin sinus magyarítására tett kísérlet volt.
Forrás: http://web.axelero.hu/pellestamas/Tamas/terminologia.htm
|
| Előzmény: [670] csocsi, 2007-03-13 16:42:54 |
|
|
| [676] Mumin | 2007-03-14 01:33:55 |
 AzO megoldása (én is segítettem):
Vegyünk két maximális távolságú pontot a sokszögben (A,B). Ha legalább az egyik belső pont (A), akkor növelni tudjuk a távolságot úgy, hogy a két ponton átmenő egyenes és a sokszög metszéspontjába visszük el A-t (természetesen B-től ellenkező irányba.) Tehát maximális távolságú pontpár csak a sokszög határán lehet.
Tegyük fel, hogy A egy oldal belső pontja. Ekkor B-től AB távolságra fekvő pontok egy körvonalon helyezkednek el, mely körvonalat az oldal érinti vagy metszi. Mindkét esetben növeljük tehát a távolságot, ha A-t mozgatjuk az oldal körvonalon kívül levő végpontjába (ilyen mindig van.) Tehát a sokszög határán elhelyezkedő pontpárok csak akkor lehetnek maximális távolságúak, ha csúcsokban vannak.
A csúcsban elhelyezkedő pontpárok közül pedig a legnagyobb távolságúnak a legnagyobb a távolsága.
|
| Előzmény: [657] HoA, 2007-02-26 16:03:28 |
|
|
| [674] BohnerGéza | 2007-03-13 20:25:33 |
 Bizonyítottnak vettem a 107. feladatot, melyet HoA [157]-ben javasolt. Így nem szükséges a gyök öt átmérőjű körökkel való lefedés. (Nem is lehet öt darabbal, esetleg ezt lehetne kitűzni feladatként.)
|
| Előzmény: [673] fermel, 2007-03-13 19:47:17 |
|
| [673] fermel | 2007-03-13 19:47:17 |
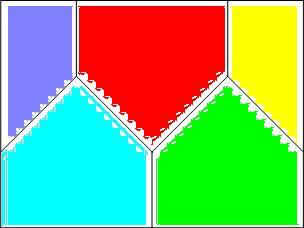
 Azt láttam, hogy öt tartomány van. A felosztás, ha nem is pontosan így, de nekem is megvolt. A problémám az, hogy mi a korrekt bizonyítása annak, hogy pld. egy "házikóban" a maximális távolság gyök öt. Tudom, hogy annyi,de ezt nekem nem sikerült tökéletesen bebizonyítanom. Gyök öt átmérőjű!! körrel kéne lefedni, de ilyet nem találtam. fermel
|
| Előzmény: [671] BohnerGéza, 2007-03-13 17:26:12 |
|
| [672] BohnerGéza | 2007-03-13 17:37:41 |
 Itt találtam: http://www.sg.hu/listazas.php3?id=1172238672
Tudtátok, hogy a nyelvújítás időszakában a sinust kebelnek akarták fordítani, a cosinus-t pótkebelnek, az arc-cosinus-t visszás-pótkebelnek. Aztán persze megbukott. Még az eredeti latin sinus szó is hibás fordítás eredménye, jelentése: öl, öböl, kebel. Az eredeti indiai szó húrt jelentet, ez arabul jiba, amiból jr-t írtak le. A középkori fordító jaib-ot értet ezalatt, ami öl vagy az öböl szája. Ebből lett a magyar kebel.
|
| Előzmény: [670] csocsi, 2007-03-13 16:42:54 |
|
| [671] BohnerGéza | 2007-03-13 17:26:12 |
 Talán megtévesztő az ábra, de csak öt szín van, tehát öt tartomány. Mivel a téglalap oldalát nem vesszük a tartományhoz, egy tartomány két pontja közt a távolság kisebb mint gyök öt.
|
| Előzmény: [669] fermel, 2007-03-13 13:10:45 |
|
| [670] csocsi | 2007-03-13 16:42:54 |
 Sziasztok! Nekem lenne egy trigonometriához kapcsolódó kérdésem. A kérdés a következő: hogy próbálták elnevezni a nyelvújítás során a szinuszfüggvényt? Ezt a kérdést órán kaptuk, és már égen földön kerestem, de még egy névhez sem tudtam kötni a kérdést sajnos. Remélem tudtok segíteni!
|
|
| [669] fermel | 2007-03-13 13:10:45 |
 Esetleg leírnád bővebben a gondolatmenetedet? Odáig rendben van, hogy az általad írtból következik az eredeti feladat megoldása,de sajnos nekem nem áll össze, hogy miért igaz, amit leírtál. Köszönöm fermel
|
| Előzmény: [662] BohnerGéza, 2007-03-05 18:01:50 |
|
| [668] Andras17 | 2007-03-09 15:48:35 |
 Kellene egy kis segítség. 2 lapot kaptam de van 4 geometriai feladat az egyiken (A geometria sajnos nem az erősségem). Itt van a feladatlap(az 1; 4; 5; 7 kellene):
http://img80.imageshack.us/img80/3689/matek0gd7.jpg
Bármilyen segítséget szivessen fogadok, mert van még egy hasonló lapom csak az meg egyenletekkel meg más feladatokkal van tele.
|
|
| [667] sakkmath | 2007-03-07 11:09:37 |
 A következő, nehéznek tűnő - még megoldatlan - feladatot én találtam ki. Minden idevágó észrevétel, ötlet, vélemény érdekelne akkor is, ha az nem párosul részleges, vagy teljes megoldással.
|
 |
|
|
|
| [664] Doom | 2007-03-05 20:23:21 |
 Mekkora a görbületi sugara egy R sugarú hengerpaláston egyenletesen ( szöggel) emelkedő csavarvonalnak? szöggel) emelkedő csavarvonalnak?
|
|
| [663] Cckek | 2007-03-05 18:25:58 |
 Helló. A következő érdekes problémákkal találkoztam a hétvégén:
1. Határozzuk meg az ABC háromszög azon belső pontját melynek a háromszög csúcsaitól mért távolságainak a szorzata maximális/minimális.
2. Határozzuk meg az ABC háromszög azon belső pontját melynek a háromszög oldalaitól mért távolságainak a szorzata maximális/minimális.
|
|














 szöggel) emelkedő csavarvonalnak?
szöggel) emelkedő csavarvonalnak?