Középiskolai Matematikai és Fizikai Lapok
Informatika rovattal
Kiadja a MATFUND Alapítvány
Már regisztráltál?
Új vendég vagy?

Fórum: GEOMETRIA

  [1]    [2]    [3]    [4]    [5]    [6]    [7]    [8]    [9]    [10]    [11]    [12]    [13]    [14]    [15]    [16]    [17]    [18]    [19]    [20]    [21]    [22]    [23]    [24]    [25]    [26]    [27]    [28]    [29]    [30]    [31]    [32]    [33]    [34]    [35]    [36]    [37]    [38]    [39]    [40]    [41]    [42]    [43]    [44]    [45]    [46]    [47]    [48]    [49]    [50]    [51]    [52]    [53]    [54]    [55]    [56]    [57]    [58]    [59]    [60]    [61]    [62]    [63]    [64]    [65]    [66]    [67]    [68]    [69]    [70]    [71]    [72]    [73]    [74]    [75]    [76]    [77]    [78]  

Szeretnél hozzászólni? Jelentkezz be.
[761] jonas2007-05-29 23:00:19

Szép bizonyítás.

Előzmény: [762] Sirpi, 2007-05-29 20:43:23
[762] Sirpi2007-05-29 20:43:23

Az állítás igaz. A bizonyítás úgy megy, hogy közelítsük mindkét konvex alakzatot zárt poligonokkal úgy, hogy a belső poligon se metssze a külsőt.

Ezután vegyük a belső sokszög egy élét, és hosszabbítsuk meg mindkét irányban. Az egyenes külső sokszöggel vett két metszéspontja két töröttvonalra osztja a külső sokszöget. Ebből dobjuk el azt, ami nem tartalmazza a belső sokszöget és helyettesítsük a meghosszabbított szakasszal. Ezzel a lépéssel a külső sokszög kerülete csökkent (valamint éleinek száma sem nőtt). Véges sok lépés során eljutunk oda, hogy a levagdosások hatására a külső és a belső sokszög megegyezik.

Azt kaptuk tehát, hogy a belső sokszög minden poligonközelítése kisebb kerületű a külső sokszög bármely poligonközelítésénél, vagyis a belső alakzat kerülete is kisebb a külsőénél.

Előzmény: [759] V Laci, 2007-05-29 17:48:47
[760] s.addam2007-05-29 19:29:33

?

[759] V Laci2007-05-29 17:48:47

Sziasztok!

Ha egy konvex síkbeli alakzat a belsejében tartalmaz egy másik konvex síkbeli alakzatot, akkor a belsőnek a kerülete kisebb mint a külsőnek.

Igaz-e az állítás? Véleményem szerint igen. De hogyan lehetne bizonyítani? A segítségeteket előre is köszönöm. Laci

[758] s.addam2007-05-29 17:11:17

Hogy lehet legkevesebb művelettel megállapítani, hogy egy kör (ismert a középpontja, és a sugara) és egy polygon (ismertek a pontjai) metszete üres halmaz-e?

[757] HoA2007-05-25 09:30:07

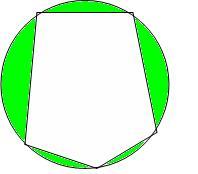
A kívánt bizonyítás egyszerű az izoperimetrikus tétel felhasználásával: Adott kerületű síkidomok közül a kör zárja be a legnagyobb területet. Állítsuk csuklós szerkezetünket húrsokszög alakúra. Rajzoljuk meg a körülírt kört. Az ábrán zölddel jelölt holdacskákat ragasszuk hozzá az oldalakhoz. A kör területe = húrsokszög területe + holdacskák területe. Ezután mozdítsuk el a csuklós szerkezetet. A keletkező idom körívekből álló kerülete megegyezik az eredeti kör kerülettel, de területe kisebb a körénél. Az idom területe = nem-húrsokszög területe + holdacskák területe. A holdacskákat levonva : nem-húrsokszög területe < húrsokszög területe. QED.

Előzmény: [756] BohnerGéza, 2007-05-24 19:45:22
[756] BohnerGéza2007-05-24 19:45:22

Fordított utat jártam be, mint HoA. Azt szeretném bizonyítani, hogy egy csuklós n-szög által bezárt terület, azaz ha egy n-szög oldalai adottak, területe akkor maximális, ha húrsokszög.

Ha csuklós n-szögünket két csúszós síklap közé rakjuk és belül fölfújuk, maximális tárfogatra, azaz alapterületre törekszik. A 114** feladatban leírt erők a nyomás miatt kialakuló a erőhatásokat helyettesítik. A 114** bizonyítása a fenti tétel "fizikai" bizonyítása. ( Erre egy, a matematikában sokszor használt, középiskolában tanult, bizonyítási módszert ajánlok. )

Előzmény: [753] HoA, 2007-05-24 11:39:17
[755] lorantfy2007-05-24 15:31:32

Kedves Cogito!

Kösz a figyelmességet és az ellenpéldát! A többi hozzászólónak is köszönet, hogy kijavítottátok ezt a hibásan megfogalmazott állítást!

Előzmény: [749] Cogito, 2007-05-23 17:09:36
[754] sakkmath2007-05-24 14:52:17

Egy idevágó részlet egy nemrégi dolgozatomból:

Előzmény: [752] HoA, 2007-05-24 11:24:52
[753] HoA2007-05-24 11:39:17

114** feladat: Igen. Geomatriai bizonyítást egyelőre nem adok, hátha más is foglalkozik a feladattal. Egy "fizikai" bizonyítás: Tegyük fel, hogy kis csuklós szerkezetünket rá tudjuk fektetni egy síkban kifeszített szappanhártyára melyet n-szögünkön belül kiszúrunk. Ekkor a hártya a rudakra a feladat feltételeiben leírt erőhatásokat fejti ki. A szappanhártya minimális felületűre akar összehúzódni. Ha tudjuk, hogy egy csuklós n-szög által bezárt terület akkor maximális ha húrsokszög, adódik, hogy a hártya csuklós szerkezetünket húrsokszöggé alakítja és ez az állapot stabil.

Előzmény: [747] BohnerGéza, 2007-05-23 00:28:23
[752] HoA2007-05-24 11:24:52

Az O1 középpontú, \lambda1 nagyítású KH1 és O2 középpontú \lambda2 nagyítású KH2 középpontos hasonlóságok KH3 szorzatának O3 középpontját éppen annak alapján könnyű meghatározni, hogy O3 a fixpont. KH1O3-t P-be viszi, ahol P=O1+\lambda1.(O3-O1) . KH2 P-t Q-ba viszi, ahol Q=O2+\lambda2.(P-O2) = (1-\lambda2).O2+\lambda2.(O1+\lambda1.(O3-O1)) . Mivel O3 fixpont, Q=O3

(1-\lambda2).O2+\lambda2.(1-\lambda1)O1+\lambda1\lambda2O3=O3

O_3 = \frac {(1-\lambda_2) \cdot O_2 + \lambda_2 \cdot ( 1 - \lambda_1 ) O_1}{1 - \lambda_1 \lambda_2}

O1ésO2 együtthatóinak összege 1, így O3 az O1O2 egyenesen van.

Előzmény: [751] Yegreg, 2007-05-23 22:34:29
[751] Yegreg2007-05-23 22:34:29

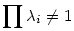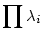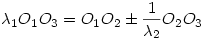Maga az az állítás, hogy középpontos hasonlóságok szorzata középpontos hasonlóság, igaz, ha \prod\lambda_i\neq 1 (ha 1 a szorzat, akkor eltolás), méghozzá tényleg \prod\lambda_i arányú, a középpontja viszont nem az, ami le volt írva. Két hasonlóság esetén a szorzat középpontja a középpontok egyenesén van, méghozzá valahogy úgy, hogy \lambda_1O_1O_3=O_1O_2\pm\frac1{\lambda_2}O_2O_3, ahol \lambda-k az arányok, O1, O2 a középpontok, O3 a szorzat középpontja. Gondolom, O3-at meg lehet adni osztóviszonyokkal is, de már késő van hozzá, hogy kitaláljam :oS Egyébként szerintem ilyenek benne vannak a Geometria és határterületeiben, de nem biztos, majd megnézem.

[750] Lóczi Lajos2007-05-23 17:20:09

Vannak még figyelmes olvasók, legyen szó akár 3 év messzeségéről is. (Micsoda véletlen egybeesés: pár perce kaptam egy levelet, hogy egy általam 3 éve jelentett szoftverproblémát kijavítottak :-)

Előzmény: [749] Cogito, 2007-05-23 17:09:36
[749] Cogito2007-05-23 17:09:36

Tisztelt lorantfy!

Idézet a [151]-es hozzászólásodból:

Az állítás általánosan is megfogalmazható: Legyen K1 O középpontú \lambda1 arányú kph. K2 pedig P középpontú \lambda2 arányú kph. Ezek egymásutáni végrehajtása helyettesíthető egy K kph-al melynek aránya \lambda=\lambda1 \lambda2 középpontja pedig az a Q pont, mely P-nek O-ra vonatkozó \lambda arányú kph. képe.

E sorokat olvasva elgondolkoztam: ha igaz ez a tétel, vajon miért nem szerepel (például) Reiman István: A geometria határterületei című könyvében, illetve más szakkönyvekben? Hosszas tűnődések után fölmerült bennem a gyanú, hogy talán azért nem említik, mert esetleg hamis ez az általánosítás?!. Ilyenkor egy dolgot tehet az ember, próbál egy ellenpéldát keresni. Némi kutakodás után bukkantam a 'tétel' következő cáfolatára:

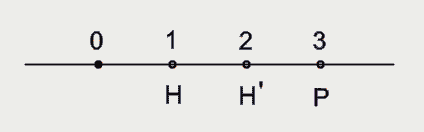
Legyen K1 az O középpontú, \lambda1=2 arányú középpontos hasonlóság, K2 pedig a P középpontú, \lambda2=2 arányú középpontos hasonlóság a következő választással: a számegyenesen az O pont legyen az origó, P legyen a 3-as pont.

Az OP szakasz O-hoz közelebbi H harmadolópontja az első nagyításnál a második harmadolópontba, H'-be kerül. Alkalmazzuk H'-re a P középpontú, \lambda2=2 arányú nyújtást. Ekkor H' képe H lesz. H tehát fixpont, ez a pont a szorzathasonlóság középpontja. A vitatott 'tétel' e konkrét esetre így szólna: P-nek O-ra vonatkozó, \lambda=4 arányú középpontos hasonlósági képe H. Ellentmondásra jutottunk, hiszen 1\ne12. A 'tétel' tehát hamis.

Ezek után kijelenthetjük: az általánosítás ilyen módon nem lehetséges (valószínűleg más módszerrel sem...). Üdvözlettel: Cogito

Előzmény: [151] lorantfy, 2004-07-16 00:54:41
[748] Iván882007-05-23 13:13:57

Ok. Akkor pontosítok. Valós függvényre gondoltam f:R\toR. Időközben rájöttem arra, hogy a sejtésem így nem igaz.

Ha az egyik aszimptota párhuzamos az y tengellyel, akkor a másik tetszőleges szöget zárhat be vele.(a ]0°;180°[ nyílt intervallumban). De mi a helyzet akkor, ha nem párhuzamos az y-tengellyel egyik aszimptota sem?

Szerintem akkor nem lehet fv. a grafikon képe, de ezt se bizonyítani se cáfolni nem tudom.

Előzmény: [745] Lóczi Lajos, 2007-05-22 10:58:49
[747] BohnerGéza2007-05-23 00:28:23

Másodszor módositott 114. feladat: Örülök, hogy HoA nem foglalkozott a feladattal. Ellenpéldája jó lett volna.

A módositott, legyen 114** feladat: Van egy n rúdból álló, a szomszédos rudakat csuklóval összekötött tömegtelen n-szögünk. Igaz-e, hogy ez n db olyan erő hatására, melyek a rudak felezőpontjában hatnak, a rudak hosszával arányosak és merőlegesek a rudakra, csakkor lehet nyugalomban, ha rúdhúrszöget alkotnak a rudak?

Nem triviális!!!

Előzmény: [746] BohnerGéza, 2007-05-22 16:27:35
[746] BohnerGéza2007-05-22 16:27:35

módositott 114. feladat: Örülök, hogy HoA foglalkozott a feladattal. Ellenpéldája jó.

A módositott, legyen 114* feladat: Van egy n rúdból álló, a szomszédos rudakat csuklóval összekötött tömegtelen n-szögünk. Igaz-e, hogy ez n db olyan erő hatására, melyek a rudak felezőpontjában hatnak és merőlegesek a rudakra, csakkor lehet nyugalomban, ha rúdhúrszöget alkotnak a rudak, az erők a rudak hosszával arányosak és erővonalaik átmennek a rúdsokszög köré írt kör középpontján?

Előzmény: [742] HoA, 2007-05-21 12:19:34
[745] Lóczi Lajos2007-05-22 10:58:49

Esetleg egy elforgatott síkbeli koordinátarendszerben!

Amúgy pl. egy zárt síkbeli körvonal is nyilván felfogható függvényként, legfeljebb nem valós-valós függvényként, hanem pl. R\toR2 függvényként, tehát a feladat megfogalmazása meglehetősen laza: meg kellene mondani, milyen halmazról melyikbe képezzen a függvényként felfogandó hozzárendelés.

Előzmény: [744] Sirpi, 2007-05-22 10:44:19
[744] Sirpi2007-05-22 10:44:19

Nem inkább az kellene, hogy az egyik aszimptota függőleges?

Előzmény: [743] Iván88, 2007-05-22 10:37:27
[743] Iván882007-05-22 10:37:27

115.feladat

Igaz-e, hogy egy hiperbola grafikonja csak akkor lehet függvény is, ha az aszimptotái merőlegesek egymásra?

[742] HoA2007-05-21 12:19:34

114. feladat: Nem. Ellenpélda az ábrán. ( képzeljük, hogy szimmetrikus :-)

Előzmény: [739] BohnerGéza, 2007-05-19 19:23:10
[741] jonas2007-05-21 10:16:41

Aha.

Akkor pedig zárt konvex halmazból is csak kontinuum sok van.

Előzmény: [740] Fálesz Mihály, 2007-05-20 15:01:24
[740] Fálesz Mihály2007-05-20 15:01:24

Egy m2 térben legfeljebb kontinuum sok nyílt halmaz lehet.

Veszel egy megszámlálható bázist, jelen esetben pl. az összes olyan nyílt téglalapot, aminek mind a 4 koordinátája racionális. Minden nyílt halmazhoz hozzárendeled az általa tartalmazott báziselemek (téglalapok) halmazát...

Zárt halmazból pedig ugyanannyi van, mint nyílt halmazból...

Előzmény: [734] jonas, 2007-05-17 15:52:16
[739] BohnerGéza2007-05-19 19:23:10

114. feladat: Talán fizika feladat? Van egy n rúdból álló, a szomszédos rudakat csuklóval összekötött tömegtelen n-szögünk. Igaz-e, hogy ez n db erő hatására csakkor lehet nyugalomban, ha rúdhúrszöget alkotnak a rudak, az erők a rudak felezőpontjában hatnak, a rudak hosszával arányosak és erővonalaik átmennek a rúdsokszög köré írt kör középpontján?

[738] Csimby2007-05-18 01:48:36

Ezek szerint rosz a megoldásom ;-)

Előzmény: [735] BohnerGéza, 2007-05-17 17:48:31

  [1]    [2]    [3]    [4]    [5]    [6]    [7]    [8]    [9]    [10]    [11]    [12]    [13]    [14]    [15]    [16]    [17]    [18]    [19]    [20]    [21]    [22]    [23]    [24]    [25]    [26]    [27]    [28]    [29]    [30]    [31]    [32]    [33]    [34]    [35]    [36]    [37]    [38]    [39]    [40]    [41]    [42]    [43]    [44]    [45]    [46]    [47]    [48]    [49]    [50]    [51]    [52]    [53]    [54]    [55]    [56]    [57]    [58]    [59]    [60]    [61]    [62]    [63]    [64]    [65]    [66]    [67]    [68]    [69]    [70]    [71]    [72]    [73]    [74]    [75]    [76]    [77]    [78]