| [787] lorantfy | 2007-06-22 15:26:24 |
 Szia HoA!
Persze, jól gondolod.
A Word-höz van MathType egyenletszerkesztőm, azzal jóval gyorsabban lehet egyenleteket írni, mint TeX-ben.
Mikor készen van kifényképezem a vágólapra Print Screen-nel aztán Paint-ben gif formátumban elmentem.
Még átlátszóvá lehetne tenni, akkor feltöltve a sárga háttérre és nem lenne keretes.
|
| Előzmény: [786] HoA, 2007-06-22 09:58:39 |
|
|
|
|
|
| [782] Cckek | 2007-06-18 21:42:27 |
 Modosítok. A gömbök diszjunktak természetesen.
|
|
|
|
| [779] Cckek | 2007-06-18 18:28:14 |
 Legalább hány gömb képes teljesen leárnyékolni egy pontszerű fényforrást? (a fényforrás nem lehet a gömbök belsejében)
|
|
| [778] HoA | 2007-06-18 16:31:00 |
 Az előző hozzászólás utolsó mondatai természetesen úgy értendők, hogy itt Q nem az ellipszis pont, hanem az F - ből e-re bocsátott merőleges és a Thálesz-kör metszéspontja.
|
| Előzmény: [777] HoA, 2007-06-18 16:25:53 |
|
| [777] HoA | 2007-06-18 16:25:53 |
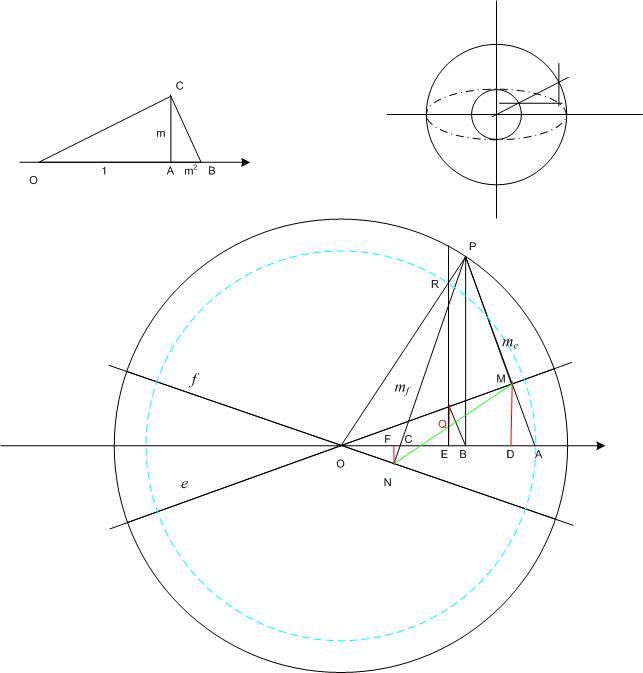
 116.és117.feladat: Két "segédtétel" : 1) Az x tengely B pontjából merőlegest bocsátunk az O-n átmenő m meredekségű egyenesre, a talppont legyen C. C merőleges vetülete az x tengelyre A. Ekkor 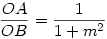 . Jelöljük ezt az arányt q-val. 2) Tekintsük ismertnek az alábbi ellipszis pontokat eredményező eljárást: A közös O középpontú k1 és k2 köröket metsző O-n áthaladó e egyenest O körül forgatjuk, a körökkel alkotott metszéspontok P1 ill. P2. A P1-n át az y tengellyel és P2-n át az x tengellyel párhuzamos egyenesek metszéspontja Q. Belátható, hogy az így adódó Q pontok egy ellipszisen találhatók. . Jelöljük ezt az arányt q-val. 2) Tekintsük ismertnek az alábbi ellipszis pontokat eredményező eljárást: A közös O középpontú k1 és k2 köröket metsző O-n áthaladó e egyenest O körül forgatjuk, a körökkel alkotott metszéspontok P1 ill. P2. A P1-n át az y tengellyel és P2-n át az x tengellyel párhuzamos egyenesek metszéspontja Q. Belátható, hogy az így adódó Q pontok egy ellipszisen találhatók.
Eredeti feladatunk r sugarú k körének P pontjából az O-n átmenő 0<m<1 meredekségű e egyenesre bocsátott me egyenes talpponja legyen M, az x tengellyel alkotott metszéspontja A. A P-ből a -m meredekségű f egyenesre bocsátott mf egyenes talpponja legyen N, az x tengellyel alkotott metszéspontja C. P merőleges vetülete az x tengelyen B. APC  egyenlőszárú, magassága PB, így OB = (OA + OC)/2. Ha M x tengelyre merőleges vetülete D, N-é F és az MN szakasz Q felezőpontjáé E, az 1. segédtétel szerint OF=q.OC, OD=q.OA, így OE=(OD+OF)/2=q.(OA+OC)/2=q.OB. QE és OP metszéspontja legyen R. OR=q.OP, Q rajta van az OP egyenes és az O középpontú, qr sugarú kör R metszéspontjából az x tengelyre bocsátott merőlegesen. egyenlőszárú, magassága PB, így OB = (OA + OC)/2. Ha M x tengelyre merőleges vetülete D, N-é F és az MN szakasz Q felezőpontjáé E, az 1. segédtétel szerint OF=q.OC, OD=q.OA, így OE=(OD+OF)/2=q.(OA+OC)/2=q.OB. QE és OP metszéspontja legyen R. OR=q.OP, Q rajta van az OP egyenes és az O középpontú, qr sugarú kör R metszéspontjából az x tengelyre bocsátott merőlegesen.
Q -nak az y tengelyre vett vetületét vizsgálva hasonló eredményre jutunk, csak ott az 1. segédtétel szerint fellépő meredekség m helyett 1/m, így az adódó kicsinyítési arány 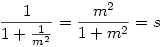 . Q rajta van az OP egyenes és az O középpontú, sr sugarú kör S metszéspontjából az y tengelyre bocsátott merőlegesen. A Q pontok tehát a 2. segédtételben leírt ellipszis pontjai, ahol a generáló körök sugarai ( az ellipszis tengelyei ) qr illetve sr. . Q rajta van az OP egyenes és az O középpontú, sr sugarú kör S metszéspontjából az y tengelyre bocsátott merőlegesen. A Q pontok tehát a 2. segédtételben leírt ellipszis pontjai, ahol a generáló körök sugarai ( az ellipszis tengelyei ) qr illetve sr.
[775] ábráján a T pont az OEP derékszögű  -ben éppen az 1. segédtételben leírt módon jön létre, tehát OT = qr = a. Mivel q+s =1, TE = OE - OT = r ( 1 - q ) = sr = b. -ben éppen az 1. segédtételben leírt módon jön létre, tehát OT = qr = a. Mivel q+s =1, TE = OE - OT = r ( 1 - q ) = sr = b.
Az f-re vonatkozó állítás téves: Legyen a [775] ábráján OE és FQ metszéspontja U. Nem QU, hanem QO lesz f-el egyenlő. Bizonyítás: Az egységsugarú OE körben 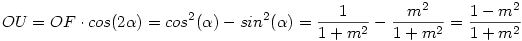 , ahol , ahol  az m meredekségű egyenes irányszöge. Az OQE derékszögű az m meredekségű egyenes irányszöge. Az OQE derékszögű  -ben OQ OU és OE = 1 mértani közepe, vagyis -ben OQ OU és OE = 1 mértani közepe, vagyis 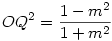 . Másrészt az ellipszisben f2=a2-b2, esetünkben . Másrészt az ellipszisben f2=a2-b2, esetünkben  . Tehát f2=OQ2 ; f = OQ . Tehát f2=OQ2 ; f = OQ
|
 |
| Előzmény: [775] BohnerGéza, 2007-06-17 22:24:45 |
|
| [776] lorantfy | 2007-06-18 14:46:29 |
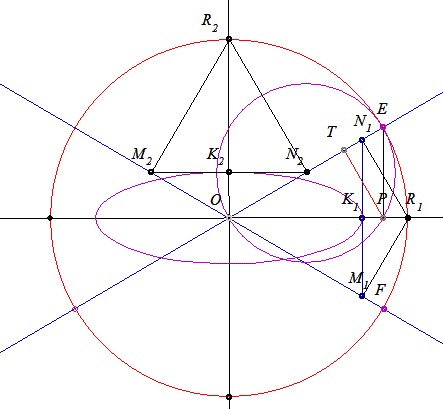
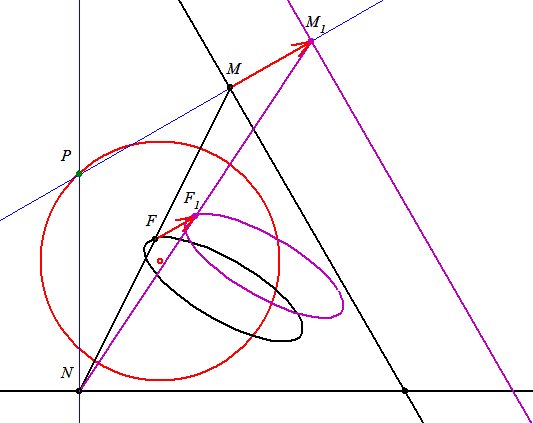
 Az ellipszis nagytengelyét r sugarú körnek az x tengellyel való R1 pontból az e és f egyenesekre bocsájtott merőlegesek talppontjait összekötő szakasz K1 felezőpontjának O-től való távolsága adja. Tehát a nagytengely OK1.
A kistengelyt hasonlóan az R2 pontból származtatva OK2 adja.
A Thálesz-körben lévő OEP háromszög egybevágó az OR1N1 és az OR2N2 háromszögekkel, mert szögeik megegyeznek és átfogójuk r hosszú. Tehát megfelelő részháromszögeik is egybevágóak.
Így az ellipszis nagytengelye: a=OK1=OT, kistengelye: b=OK2=TE. Tehát r=a+b.
|
 |
| Előzmény: [775] BohnerGéza, 2007-06-17 22:24:45 |
|
| [775] BohnerGéza | 2007-06-17 22:24:45 |
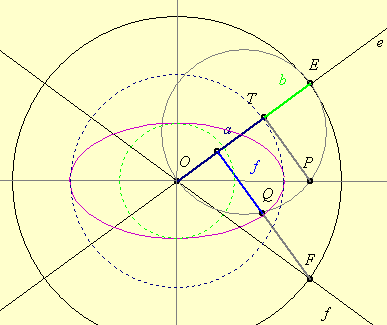
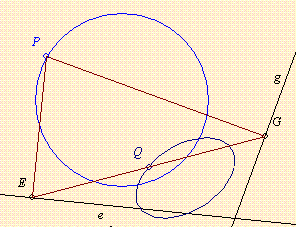
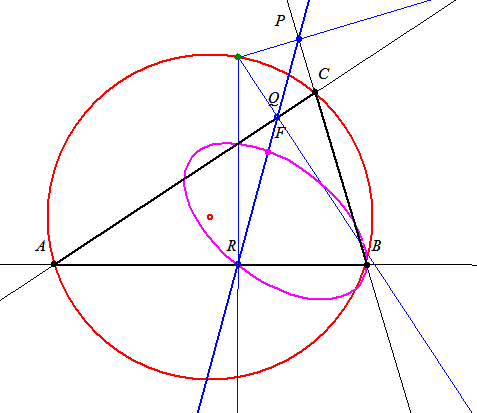
 117. feladat: Használjuk föl, hogy a 116. feladat mértani helye ellipszis! Bizonyítsuk, hogy ennek két (fél)tengelye és a (fél)fókusztávolság megszerkeszthető az ábrán látott módon! ( A [774]-es hozzászólás számolási eredményeinek használata nem szükséges! )
A két adott egyenes e és f, az adott kör sugara egyenlő az ábra OE szakaszával. Válasszuk úgy a jelöléseket, hogy az FOE szög ne legyen nagyobb derékszögnél, messe az OE Thálesz-köre FOE szögfelezőjét P-ben. A P-ből e-re állított merőleges talppontja T. Tehát igazolandó, hogy a=OT, b=TE, valamint az F-ből e-re állított merőleges szakasznak a Thálesz-körbe eső része f!
|
 |
|
|
|
|
|
|
| [769] lorantfy | 2007-06-11 21:08:34 |
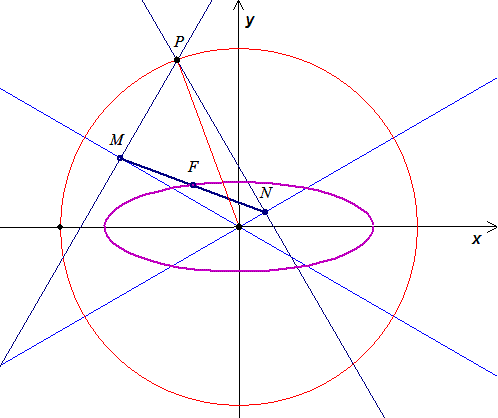
 Nézzünk először egy spec. esetet. Amikor a két egyenes, AB és BC merőlegesek egymásra. Ekkor a talppontok felezőpontja egyben PB szakasz felezőpontja is. Igy a keresett mértani hely a kör B középpontú felére kicsinyített képe.
|
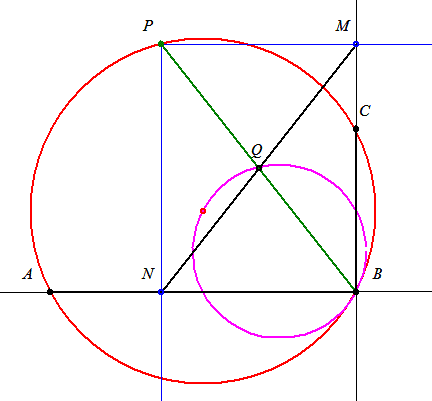 |
| Előzmény: [767] BohnerGéza, 2007-06-06 22:32:11 |
|
|
| [767] BohnerGéza | 2007-06-06 22:32:11 |
 Nagyon szép észrevétel, de mielőtt valaki összekapcsolná a Simson-egyenessel:
klevente feladata, 116. feladat: Adott egy kör és két egyenes. A kör P pontjából állítsunk merőlegest az egyenesekre, a talppontok közti felezőpont legyen Q. Bizonyitandó, a Q pontok mértani helye ellipszis, ha P végigfut a körön.
|
| Előzmény: [765] klevente, 2007-06-06 14:17:45 |
|
|
| [765] klevente | 2007-06-06 14:17:45 |
 Egy háromszög köré írt kör tetszőleges P pontjából állítsunk merőlegeseket a háromszög oldalegyeneseire. Közismert, hogy ezen merőlegesek talppontjai kollineárisak, ez az ún. Simson-egyenes.
Vizsgáljuk valamelyik két talppont összekötő szakasza felezőpontjának mértani helyét, ha P befutja a köréírt kört. A GeoGebra programmal nézve ez szinte bizonyosan ellipszis.
Kérdések: a) tud-e valaki arról, hogy ez a tény (sejtés) ismertnek számít-e a matematikában? b) tudná-e valaki bizonyítani vagy cáfolni?
Koncz Levente
|
|
| [764] HoA | 2007-05-31 22:11:09 |
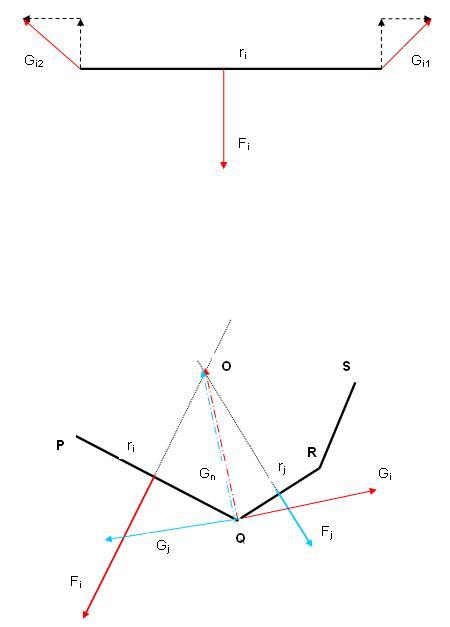
 114** feladat Vizsgáljuk az li hosszúságú ri rúdra ható erőket. A rúdra hat a feladatban adott Fi külső erő és a csuklókban a szomszédos rudak Gi1 és Gi2 kényszerereje. Bontsuk fel az erőket rúdirányú és a rúdra merőleges összetevőkre. Gi1 és Gi2 rúdirányú összetevői egymás ellentettjei, mert a rúd nyugalomban van és más rúdirányú erő nem hat rá. Gi1 és Gi2 rúdra merőleges összetevői egyenlőek és 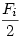 nagyságúak, mert a rúd másik végére vonatkozó nyomatékuk li karon egyensúlyt tart Fi erő nagyságúak, mert a rúd másik végére vonatkozó nyomatékuk li karon egyensúlyt tart Fi erő 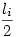 karon kifejtett nyomatékával. Megállapíthatjuk tehát, hogy Gi1 és Gi2 egyenlő nagyságűak. Mivel a csuklókban a rudak azonos nagyságú erővel hatnak egymásra, a szomszédos rúdra hatő kényszererő is akkora, mint Gi1 és Gi2 és így tovább : az összes csuklóban ugyanakkora erők hatnak. Legyen ennek az erőnek a nagysága G. karon kifejtett nyomatékával. Megállapíthatjuk tehát, hogy Gi1 és Gi2 egyenlő nagyságűak. Mivel a csuklókban a rudak azonos nagyságú erővel hatnak egymásra, a szomszédos rúdra hatő kényszererő is akkora, mint Gi1 és Gi2 és így tovább : az összes csuklóban ugyanakkora erők hatnak. Legyen ennek az erőnek a nagysága G.
Tekintsük a szomszédos, li és lj hosszúságú ri és rj rudakra ható erőket. Válasszuk úgy az ábrán az erő mértékegységét, hogy a rúd hosszával arányos Fi és Fj erőket éppen li és lj hosszú vektorral ábrázoljuk. Az ri rúdra a Q csuklóban ható Gi erő rúdra merőleges összetevője Fi/2=li/2 . Rajzoljuk meg Q-ban a sokszög belseje felé mutató, Gi-re merőleges, G hosszúságú Gn vektort, Gi 90 fokos elforgatottját. Ennek ri irányába eső összetevője li/2, tehát O végpontja rajta van ri felező merőlegesén. De a Gn vektort úgy is tekinthetjük, mint az rj rúdra Q-ban ható Gj erö -90 fokos elforgatottját. Mivel Gj erö rj -re merőleges összetevője lj/2 nagyságú, Gn -nek rj irányába eső összetevője is ekkora, vagyis O rajta van rj felező merőlegesén is. Vagyis a P,Q,R pontok egy G sugarú körön vannak. A gondolatmenetet a következő R csuklóra alkalmazva azt kapjuk, hogy a Q,R, S pontok is egy G sugarú körön vannak. A két kör azonos: középpontjuk QR felező merőlegesén a sokszög belseje felé Q-tól és R-től G távolságra lévő O pont. Az eljárást folytatva adódik, hogy a csuklók húrsokszöget alkotnak.
|
 |
| Előzmény: [747] BohnerGéza, 2007-05-23 00:28:23 |
|
|







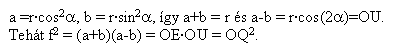

 egyenlőszárú, magassága PB, így OB = (OA + OC)/2. Ha M x tengelyre merőleges vetülete D, N-é F és az MN szakasz Q felezőpontjáé E, az 1. segédtétel szerint OF=q.OC, OD=q.OA, így OE=(OD+OF)/2=q.(OA+OC)/2=q.OB. QE és OP metszéspontja legyen R. OR=q.OP, Q rajta van az OP egyenes és az O középpontú, qr sugarú kör R metszéspontjából az x tengelyre bocsátott merőlegesen.
egyenlőszárú, magassága PB, így OB = (OA + OC)/2. Ha M x tengelyre merőleges vetülete D, N-é F és az MN szakasz Q felezőpontjáé E, az 1. segédtétel szerint OF=q.OC, OD=q.OA, így OE=(OD+OF)/2=q.(OA+OC)/2=q.OB. QE és OP metszéspontja legyen R. OR=q.OP, Q rajta van az OP egyenes és az O középpontú, qr sugarú kör R metszéspontjából az x tengelyre bocsátott merőlegesen.  az m meredekségű egyenes irányszöge. Az OQE derékszögű
az m meredekségű egyenes irányszöge. Az OQE derékszögű 


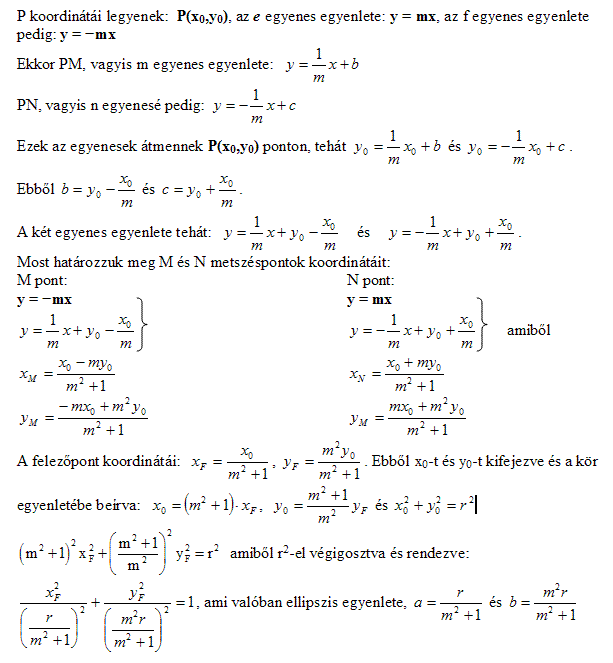
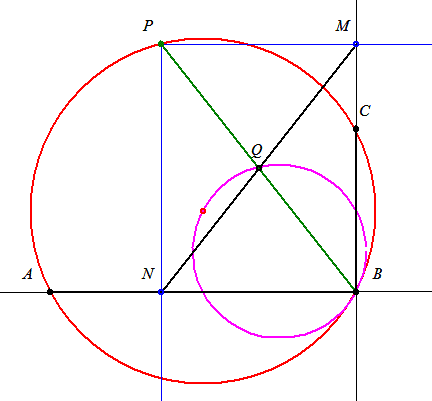



 ) az alakzat szélességfüggvénye, azaz w(
) az alakzat szélességfüggvénye, azaz w(