|
|
|
| [910] Cckek | 2007-10-21 07:31:36 |
 Az ABC háromszögben mA=100o,mB=40o,mC=40o. Az AB oldalt meghosszabbítjuk BD=BC-AB-vel. Határozzuk meg az ADC szög mértékét.
|
|
| [909] farkasb | 2007-10-16 21:09:35 |
 Ezt a hozzászólást és levezetést is köszönöm!
|
|
|
|
|
|
| [904] HoA | 2007-10-16 16:34:08 |
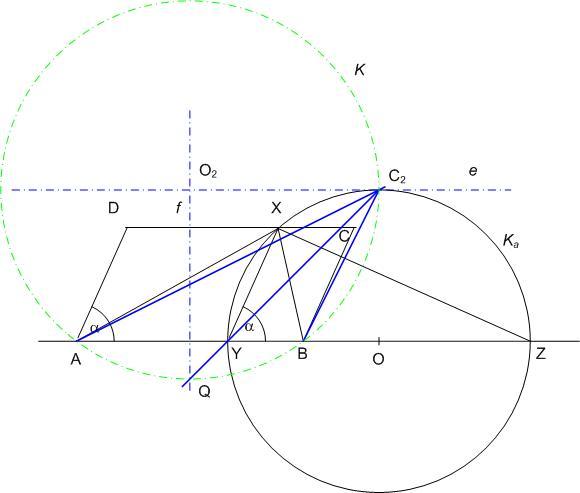
 Legyen adott a paralellogramma az a, b,  adatokkal. A szerkesztendő X ill. Y pontok [885] szerint. A Ka Apolloniusz-kör átmérője d=b/cos adatokkal. A szerkesztendő X ill. Y pontok [885] szerint. A Ka Apolloniusz-kör átmérője d=b/cos és ra=d/2 sugara szintén adottnak tekinthető. Érintse az AB-vel párhuzamos e egyenes Ka-t C2-ben. Ka minden pontjára, így C2-re is igaz, hogy az AC2B és ra=d/2 sugara szintén adottnak tekinthető. Érintse az AB-vel párhuzamos e egyenes Ka-t C2-ben. Ka minden pontjára, így C2-re is igaz, hogy az AC2B felezője AB-t Y-ban metszi. Legyen ABC2 felezője AB-t Y-ban metszi. Legyen ABC2 körülírt K körének sugara R, középpontja O2. Tudjuk, hogy a belső szögfelező a szemközti oldal felező merőlegesét a körülírt körön metszi. Legyen C2Y és K metszéspontja Q. QC2O2 körülírt K körének sugara R, középpontja O2. Tudjuk, hogy a belső szögfelező a szemközti oldal felező merőlegesét a körülírt körön metszi. Legyen C2Y és K metszéspontja Q. QC2O2 egyenlőszárú, mert C2O2=QO2=R. C2QO2 egyenlőszárú, mert C2O2=QO2=R. C2QO2 =OC2Y =OC2Y =45 fok, tehát QO2C2 =45 fok, tehát QO2C2 =90 fok, ami azt jelenti, hogy O2 e-n van. =90 fok, ami azt jelenti, hogy O2 e-n van.
Innen az alábbi szerkesztés adódik: Az a hosszúságú AB szakasszal párhuzamosan, tőle ra távolságra vegyük fel az e egyenest. AB f felező merőlegesének és e-nek a metszéspontja O2. Az O2 középpontú, R=O2A sugarú K kör és e (egyik) metszéspontja C2, K és f metszéspontja ( e egyenes AB-t tartalmazó oldalán ) Q. C2Q kimetszi AB-ből Y-t.
|
 |
| Előzmény: [890] HoA, 2007-10-11 18:08:18 |
|
|
| [902] farkasb | 2007-10-16 15:13:47 |
 Megpróbálom magyarul :)
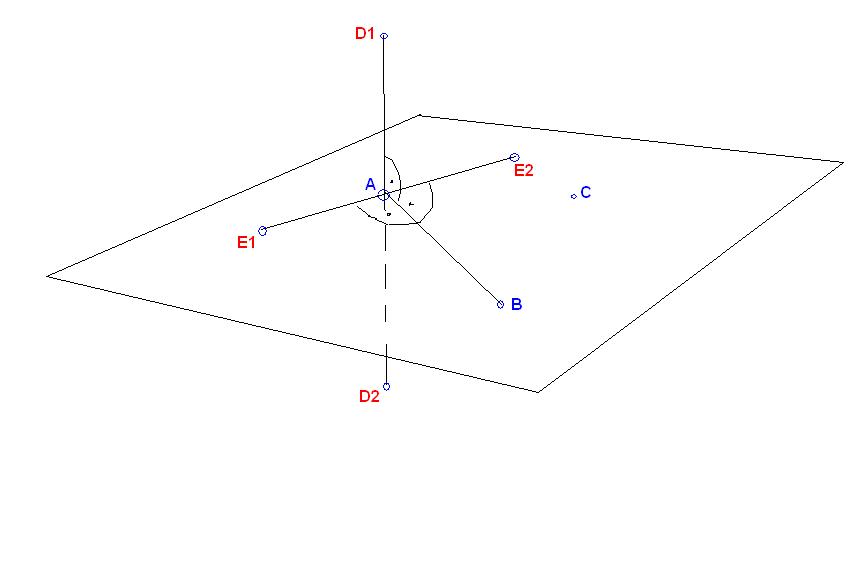
Adott ABC pont xyz koordinátákkal. Keresett 4 db pont. -Az első kettő (D1, D2), amelyik az BA szakaszra merőleges, B-től mért távolsága +10, -10 egység, és a BD1, BD2 merőleges az ABC síkra. A másik kettő (E1, E2)pedig ugyancsak merőleges a BA szakaszra, de az ABC síkon van, és B-től mért távolsága 10 e. Itt egy szemléltető ábra is. Előre is köszönet!
|
 |
|
| [901] HoA | 2007-10-16 14:19:52 |
 Első kérdés : (ld. BohnerGézáé) Az ABC síkra merőleges vetítésre gondolsz?
Második kérdés: AZ ABC síkban fekvő, B-nél derékszögű ABC*  C* csúcsát keresed, ahol BC* = 10 egység? C* csúcsát keresed, ahol BC* = 10 egység?
|
| Előzmény: [899] farkasb, 2007-10-16 12:06:35 |
|
| [900] BohnerGéza | 2007-10-16 14:12:04 |
 Nem érthető (számomra) a feladat! Azt a részt, hogy egy pont legyen merőleges egy szakaszra, azt valószínűleg más sem érti.
Az elején merőleges vetítés van?
Fogalmazd meg jól a feladatot, talán tudunk segíteni.
|
| Előzmény: [899] farkasb, 2007-10-16 12:06:35 |
|
| [899] farkasb | 2007-10-16 12:06:35 |
 Kedves Fórumozók!
Ilyen nehezet kérdeztem (nem hinném), vagy túl egyszerű? Megköszönném, ha valaki tudna segíteni.
|
|
| [898] farkasb | 2007-10-14 23:16:22 |
 Egy újabb, elvileg egyszerű kérdésem lenne. Adott A B C pont a térben. -Hogyan határozhatom meg azt a pontot(pontokat), mely az ABC síkra vetítve a vetítősugár a B ponton menne át, és B ponttól 10 egységnyire van. -továbbá szükség lenne arra a pontra (pontokra), amelyik AB szakaszra merőleges, és a ABC síkon helyezkedik el, és B pontból indul, és 10 egységnyire van tőle. Előre is köszönet!
|
|
|
|
| [895] Hajba Károly | 2007-10-13 01:03:02 |
 Amilyen arányban növelem a négyzet kerületét, olyan arányban nő az oldalhossza is. Így elég csak az egyik oldalhosszat vizsgálni. Megnövelem 4 méterrel, de ez egyben azt is jelenti, hogy a háromszorosára nőt. Ha valamit háromszorosára növelek, az azt jelenti, hogy még kétszer hozzáadom önmagához (1+2=3). Azaz a 4 méter az eredeti hossz kétszerese, így az eredeti hossz a 4 méter fele, azaz 2 méter.
|
| Előzmény: [894] Emilio, 2007-10-12 23:42:25 |
|
| [894] Emilio | 2007-10-12 23:42:25 |
 Ha egy négyzet olkdalhosszát4m -rel növeljük,kerülete háromszorosára nő.mekkora az eredeti négyzet oldalhossza?
|
|
| [893] HoA | 2007-10-12 20:27:30 |
 Bocs , az utolsó mondat helyesen : "Ekkor az egész A*CB'  és az ennek A*C oldalán fekvő A' pont is f -nek ezen az oldalán van,..." és az ennek A*C oldalán fekvő A' pont is f -nek ezen az oldalán van,..."
|
| Előzmény: [892] HoA, 2007-10-12 20:18:06 |
|
| [892] HoA | 2007-10-12 20:18:06 |
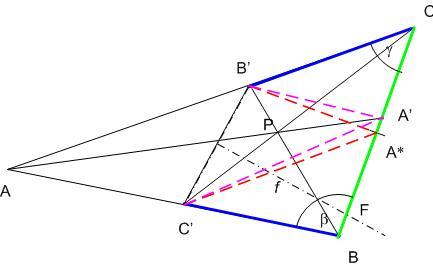
 Belátjuk, hogy ha a  nem egyenlőszárú, pontosabban ha AB nem egyenlőszárú, pontosabban ha AB AC , akkor BC'=CB' és B'A'=C'A' egyszerre nem állhat fenn. Legyen az ABC AC , akkor BC'=CB' és B'A'=C'A' egyszerre nem állhat fenn. Legyen az ABC -ben AC>AB, CB'=BC', BB' és CC' metszéspontja P, PA és BC metszéspontja A'. A Ceva tétel szerint BA'.CB'.AC'=A'C.B'A.C'B CB' = C'B -vel egyszerűsítve BA'.AC'=A'C.B'A . AC>AB miatt B'A>AC' és így A'C<BA' , vagyia A' a BC oldal A* felezőpontja és C között van. -ben AC>AB, CB'=BC', BB' és CC' metszéspontja P, PA és BC metszéspontja A'. A Ceva tétel szerint BA'.CB'.AC'=A'C.B'A.C'B CB' = C'B -vel egyszerűsítve BA'.AC'=A'C.B'A . AC>AB miatt B'A>AC' és így A'C<BA' , vagyia A' a BC oldal A* felezőpontja és C között van.
A C'BA* és az A*CB'  két oldalban megegyezik, de a közrezárt szög - mint az ABC két oldalban megegyezik, de a közrezárt szög - mint az ABC  nagyobb oldalával szemközti szög - az előbbiben ( nagyobb oldalával szemközti szög - az előbbiben ( ) nagyobb mint az utóbbiban ( ) nagyobb mint az utóbbiban ( ) . Ezért a cosinus tétel szerint C'A*>B'A*. A* tehát a B'C' f felező merőlegesének ugyanazon az oldalán van, mint B'. Ekkor az egész A*BC' ) . Ezért a cosinus tétel szerint C'A*>B'A*. A* tehát a B'C' f felező merőlegesének ugyanazon az oldalán van, mint B'. Ekkor az egész A*BC'  és az ennek A*C oldalán fekvő A' pont is f -nek ezen az oldalán van, vagyis B'-höz közelebb, mint C' -höz , A'B'<A'C' , amit bizonyítani akartunk. és az ennek A*C oldalán fekvő A' pont is f -nek ezen az oldalán van, vagyis B'-höz közelebb, mint C' -höz , A'B'<A'C' , amit bizonyítani akartunk.
|
 |
| Előzmény: [889] Gyöngyő, 2007-10-11 17:35:44 |
|
| [891] Sz_Z | 2007-10-11 23:36:42 |
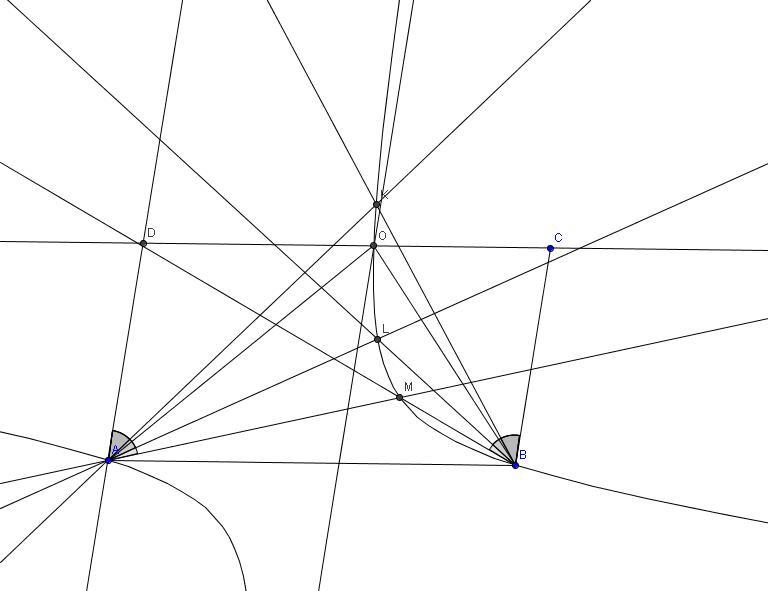
 Itt egy "szerkesztő megoldás", igaz, használ némi projektív geometriát. A [874] hozzászólás alapján olyan egyeneseket keresünk az A és B pontokon keresztül, amelyek "száraktól mért dőlésszöge egyenlő ellentétes irányban" (1), és a metszéspontjuk CD-n van. Az (1) tulajdonságú egyenesek - mivel egymáshoz projektív, A ill. B tartójú sugársorok egymásnak megfelelő egyenesei - metszéspontjai egy hiperbolán vannak, melyre A és B illeszkedik. Ha ennek a hiperbolának három további tetszőleges pontját megszerkesztjük (K, L, M), akkor a hiperbola és a CD egyenes metszéspontjai szerkeszthetőek. (Természetesen ezt a szerkesztést - Steiner-szerkesztés - körzővel-vonalzóval picit hosszabb megcsinálni, mint géppel.)
|
 |
|
| [890] HoA | 2007-10-11 18:08:18 |
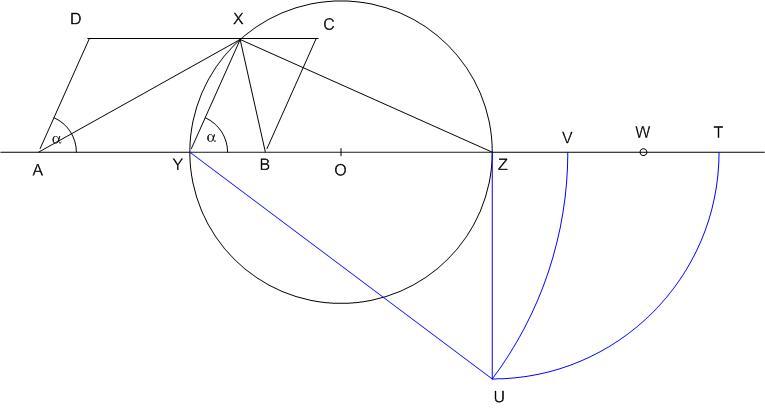
 Amíg nem születik igazi szerkesztő megoldás, addig itt van egy , az eddigieknél talán egyszerűbb, számítást követő szerkesztés.
Legyen adva a paralellogramma az AB = a , BC = b oldalhosszakkal és az A-nál lévő  szöggel. Vegyük fel az ABX szöggel. Vegyük fel az ABX  Apollonius körét. Középpontja legyen O, Y-nal szemközti pontja Z. Az XYZ derékszögű Apollonius körét. Középpontja legyen O, Y-nal szemközti pontja Z. Az XYZ derékszögű  ből YZ=d=b/cos ből YZ=d=b/cos , ami adatainkból számítható/szerkeszthető. Mivel az Apollonius kör pontjaira az A-tól és B-től mért távolságok aránya állandó, YB-t x-el jelölve felírható : , ami adatainkból számítható/szerkeszthető. Mivel az Apollonius kör pontjaira az A-tól és B-től mért távolságok aránya állandó, YB-t x-el jelölve felírható :
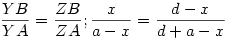
Rendezve x-re másodfokú egyenletet kapunk, melynek megoldása: 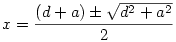 Mivel x a-nál és d-nél is rövidebb, ezért Mivel x a-nál és d-nél is rövidebb, ezért 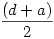 -nél is, tehát csak a negatív előjelet kell figyelembe venni. x szerkeszthető pl így: Vegyük fel a d hosszúságú YZ Z-n túli meghosszabbítására az a hosszúságú ZT szakaszt. Z-ben emeljünk merőlegest YT-re, forgassuk rá Z-ből ZT-t, a metszéspont legyen U. Ekkor -nél is, tehát csak a negatív előjelet kell figyelembe venni. x szerkeszthető pl így: Vegyük fel a d hosszúságú YZ Z-n túli meghosszabbítására az a hosszúságú ZT szakaszt. Z-ben emeljünk merőlegest YT-re, forgassuk rá Z-ből ZT-t, a metszéspont legyen U. Ekkor 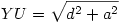 , ezt Y-ból leforgatva YT-re a metszéspont legyen V. Ha W a VT szakasz felezőpontja, VW = WT = x. , ezt Y-ból leforgatva YT-re a metszéspont legyen V. Ha W a VT szakasz felezőpontja, VW = WT = x.
|
 |
| Előzmény: [881] BohnerGéza, 2007-10-10 22:47:04 |
|
| [889] Gyöngyő | 2007-10-11 17:35:44 |
 Sziasztok!
Tudnátok segíteni a következő feladatban:
Adva van egy egy háromszög,felveszünk benne egy p pontot. Összekötjük a csúcsokat a szembelévő oldallal a p ponton keresztül.A metszéspontok rendre A', B',C'. Tudjuk továbbá,hogy C(B)'=B(C)',vmint B'A'=A'C'. Mutassuk meg h a háromszög egyenlőszárú.
Köszönettel: Zsolt
|
|










 10.n0.
10.n0.  adatokkal. A szerkesztendő X ill. Y pontok [885] szerint. A Ka Apolloniusz-kör átmérője d=b/cos
adatokkal. A szerkesztendő X ill. Y pontok [885] szerint. A Ka Apolloniusz-kör átmérője d=b/cos felezője AB-t Y-ban metszi. Legyen ABC2
felezője AB-t Y-ban metszi. Legyen ABC2 körülírt K körének sugara R, középpontja O2. Tudjuk, hogy a belső szögfelező a szemközti oldal felező merőlegesét a körülírt körön metszi. Legyen C2Y és K metszéspontja Q. QC2O2
körülírt K körének sugara R, középpontja O2. Tudjuk, hogy a belső szögfelező a szemközti oldal felező merőlegesét a körülírt körön metszi. Legyen C2Y és K metszéspontja Q. QC2O2


 AC , akkor BC'=CB' és B'A'=C'A' egyszerre nem állhat fenn. Legyen az ABC
AC , akkor BC'=CB' és B'A'=C'A' egyszerre nem állhat fenn. Legyen az ABC ) nagyobb mint az utóbbiban (
) nagyobb mint az utóbbiban ( ) . Ezért a cosinus tétel szerint C'A*>B'A*. A* tehát a B'C' f felező merőlegesének ugyanazon az oldalán van, mint B'. Ekkor az egész A*BC'
) . Ezért a cosinus tétel szerint C'A*>B'A*. A* tehát a B'C' f felező merőlegesének ugyanazon az oldalán van, mint B'. Ekkor az egész A*BC' 



