|
|
| [919] Cckek | 2007-10-25 23:02:49 |
 Köszönöm mindkettőtöknek, HoA és Bohner Géza ezeket az érdekes hozzászolásokat, nekem is van egy "csúnya" trigonometrikus megoldásom, de ez nem vetekszik egyikötök megoldásával sem. Köszi.
|
|
| [918] farkasb | 2007-10-25 22:59:45 |
 Kedves Fórumozók!
Lenne egy újabb kérdésem/problémám.
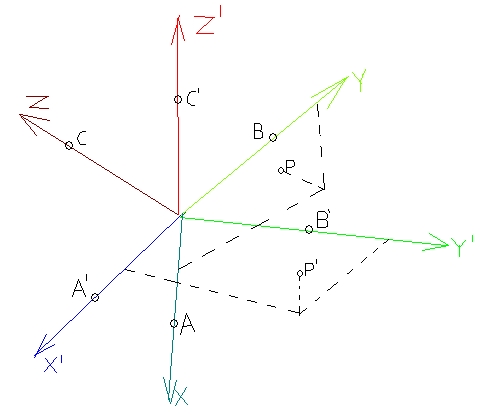
Térbeli koordináta transzformációl lenne szó.
Adott két derékszögű koordináta rendszer, és egy P pont.
Az eredeti koordináta rendszer origója (0,0,0)
X tengelyén A (29.955,2,556,-39,952) //50 egységre O-tól
Y tengelyén B (10.063,47,815,10,604) //50 egységre O-tól
Z tengelyén C (38.748,-14.393,28.132) //50 egységre O-tól
P(20.653,53.039,4,877)
A cél koordináta rendszer origója szintén (0,0,0)
X tengelyén A' (50,0,0)
Y tengelyén B' (0,50,0)
Z tengelyén C' (0,0,50)
Keresett a P pont cél koordináta rendszer beli x,y,z koordinátája.
3dStudio Max porgrammal csináltam meg fordítva az egészet, és a keresett P' pont koordinátái: (10,30,15)
Próbáltam kiszámolni ezt a forgatást, de sehogy sem jött össze. Ezért kérnék némi segítséget.
Ezeket a képleteket használtam:
r11= cos(gamma)*cos(béta)
r12= cos(gamma)*sin(béta)*sin(alfa)-sin(gamma)*cos(alfa)
r13= cos(gamma)*sin(béta)*cos(alfa)+sin(gamma)*sin(alfa)
r21= sin(gamma)*cos(béta)
r22= sin(gamma)*sin(béta)*sin(alfa)+cos(gamma)*cos(alfa)
r23= sin(gamma)*sin(gamma)*sin(béta)*cos(alfa)-cos(gamma)*sin(alfa)
r31= -sin(béta)
r32= cos(béta)*sin(alfa)
r33= cos(béta)*cos(alfa)
P'x= r11* Px+ r12* Py+ r13* Pz
P'y= r21* Px+ r22* Py+ r23* Pz
P'z= r31* Px+ r32* Py+ r33* Pz
Előre is köszönöm a segítséget!
|
|
| [917] HoA | 2007-10-25 19:19:39 |
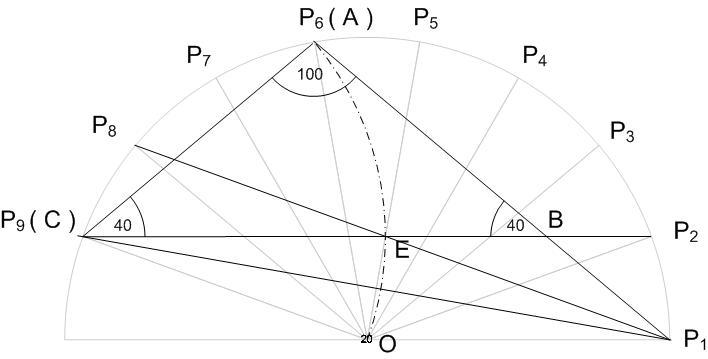
 A KöMaL régebbi olvasói számára ismert, hogy az ilyen feladatok megoldásához, ahol a  -ek szögei 10o egész számú többszörösei, jól használható a szabályos 18-szög oldalaiból, átlóiból és körülírt K köréből álló H18 hálózat. Ha ívhossz egységnek K két szomszédos csúcs közötti ívét vesszük, n egységnyi ívhez n.10o kerületi és n.20o középponti szög tartozik. -ek szögei 10o egész számú többszörösei, jól használható a szabályos 18-szög oldalaiból, átlóiból és körülírt K köréből álló H18 hálózat. Ha ívhossz egységnek K két szomszédos csúcs közötti ívét vesszük, n egységnyi ívhez n.10o kerületi és n.20o középponti szög tartozik.
Legyenek H18 csúcsai P1,.., P18, K középpontja O, sugara R. Húzzuk be a P1P6, P2P9 és P6P9 átlókat. Legyen A=P6,C=P9 , B pedig P1P6 és P2P9 metszéspontja. Ekkor ABC a feladatban szereplő  , hiszen P1P6P9 , hiszen P1P6P9 =100o és P2P9P6 =100o és P2P9P6 =40o. =40o.
OP6P9 R oldalú szabályos  . Legyen a C középpontú R sugarú kör és a BC szakasz metszéspontja E. Ekkor BE a feladatban szereplő oldalhossz különbség. OCE egyenlőszárú . Legyen a C középpontú R sugarú kör és a BC szakasz metszéspontja E. Ekkor BE a feladatban szereplő oldalhossz különbség. OCE egyenlőszárú  csúcsszöge 60o-40o=20o, COE csúcsszöge 60o-40o=20o, COE =80o , E rajta van az OP5 sugáron. De akkor E a P2P9 átló e sugárra vett tükörképén, P1P8 -on is rajta van. A BP1E =80o , E rajta van az OP5 sugáron. De akkor E a P2P9 átló e sugárra vett tükörképén, P1P8 -on is rajta van. A BP1E -ben BP1E -ben BP1E =P6P1P8 =P6P1P8 =20o, a B-nél lévő külső szög 40o, P1BE =20o, a B-nél lévő külső szög 40o, P1BE egyenlőszárú, így P1 feladatunk D pontja. ADC egyenlőszárú, így P1 feladatunk D pontja. ADC =P6P1P9 =P6P1P9 =30o. =30o.
|
 |
| Előzmény: [910] Cckek, 2007-10-21 07:31:36 |
|
|
|
| [914] Draskóczy Gergely | 2007-10-24 16:30:12 |
 Munkám során merült föl az alábbi probléma:
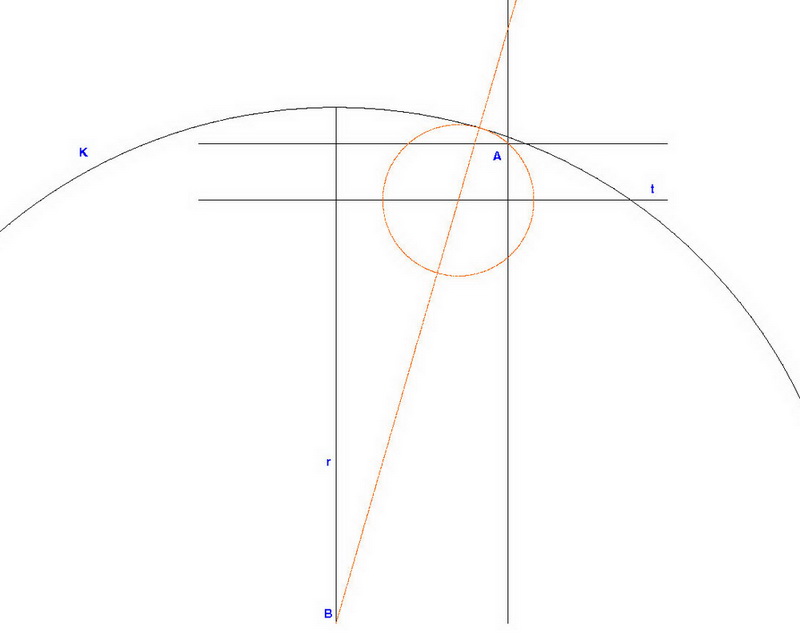
adott A pont, K kör, t egyenes
szerkesszünk geometriai úton olyan kört (2 is van) mely átmegy A ponton, középpontja t egyenesen van, érinti a K kört
Tud ebben valaki segíteni?
Gergő
|
 |
|
|
|
|
|
| [910] Cckek | 2007-10-21 07:31:36 |
 Az ABC háromszögben mA=100o,mB=40o,mC=40o. Az AB oldalt meghosszabbítjuk BD=BC-AB-vel. Határozzuk meg az ADC szög mértékét.
|
|
| [909] farkasb | 2007-10-16 21:09:35 |
 Ezt a hozzászólást és levezetést is köszönöm!
|
|
|
|
|
|
| [904] HoA | 2007-10-16 16:34:08 |
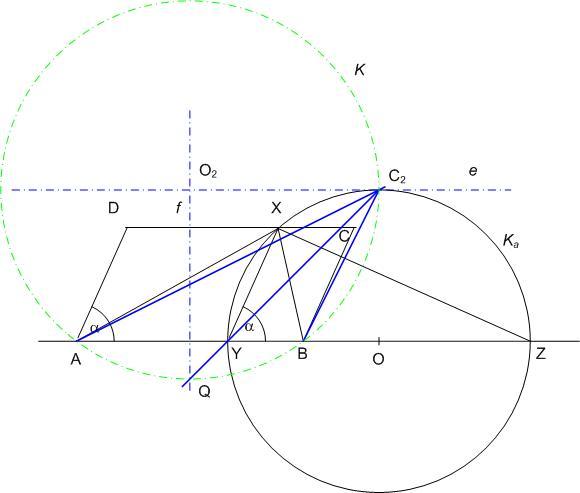
 Legyen adott a paralellogramma az a, b,  adatokkal. A szerkesztendő X ill. Y pontok [885] szerint. A Ka Apolloniusz-kör átmérője d=b/cos adatokkal. A szerkesztendő X ill. Y pontok [885] szerint. A Ka Apolloniusz-kör átmérője d=b/cos és ra=d/2 sugara szintén adottnak tekinthető. Érintse az AB-vel párhuzamos e egyenes Ka-t C2-ben. Ka minden pontjára, így C2-re is igaz, hogy az AC2B és ra=d/2 sugara szintén adottnak tekinthető. Érintse az AB-vel párhuzamos e egyenes Ka-t C2-ben. Ka minden pontjára, így C2-re is igaz, hogy az AC2B felezője AB-t Y-ban metszi. Legyen ABC2 felezője AB-t Y-ban metszi. Legyen ABC2 körülírt K körének sugara R, középpontja O2. Tudjuk, hogy a belső szögfelező a szemközti oldal felező merőlegesét a körülírt körön metszi. Legyen C2Y és K metszéspontja Q. QC2O2 körülírt K körének sugara R, középpontja O2. Tudjuk, hogy a belső szögfelező a szemközti oldal felező merőlegesét a körülírt körön metszi. Legyen C2Y és K metszéspontja Q. QC2O2 egyenlőszárú, mert C2O2=QO2=R. C2QO2 egyenlőszárú, mert C2O2=QO2=R. C2QO2 =OC2Y =OC2Y =45 fok, tehát QO2C2 =45 fok, tehát QO2C2 =90 fok, ami azt jelenti, hogy O2 e-n van. =90 fok, ami azt jelenti, hogy O2 e-n van.
Innen az alábbi szerkesztés adódik: Az a hosszúságú AB szakasszal párhuzamosan, tőle ra távolságra vegyük fel az e egyenest. AB f felező merőlegesének és e-nek a metszéspontja O2. Az O2 középpontú, R=O2A sugarú K kör és e (egyik) metszéspontja C2, K és f metszéspontja ( e egyenes AB-t tartalmazó oldalán ) Q. C2Q kimetszi AB-ből Y-t.
|
 |
| Előzmény: [890] HoA, 2007-10-11 18:08:18 |
|
|
| [902] farkasb | 2007-10-16 15:13:47 |
 Megpróbálom magyarul :)
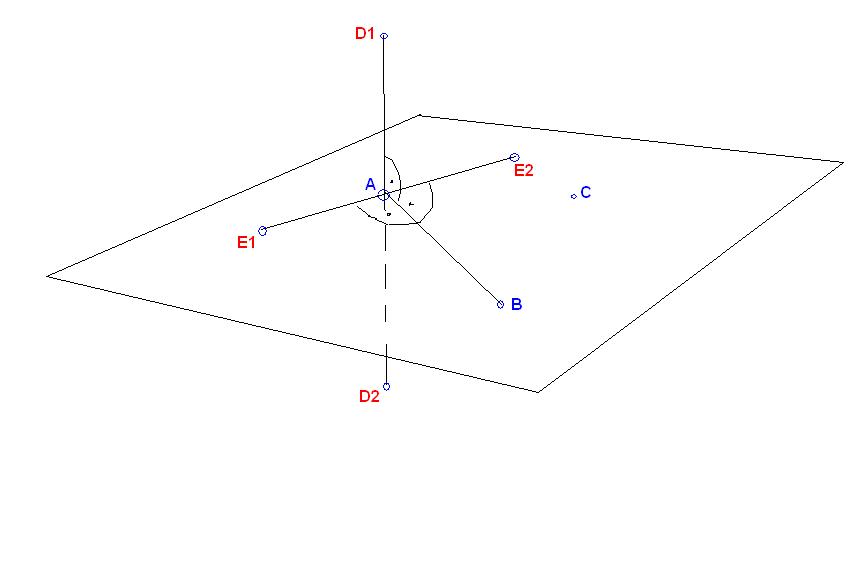
Adott ABC pont xyz koordinátákkal. Keresett 4 db pont. -Az első kettő (D1, D2), amelyik az BA szakaszra merőleges, B-től mért távolsága +10, -10 egység, és a BD1, BD2 merőleges az ABC síkra. A másik kettő (E1, E2)pedig ugyancsak merőleges a BA szakaszra, de az ABC síkon van, és B-től mért távolsága 10 e. Itt egy szemléltető ábra is. Előre is köszönet!
|
 |
|
| [901] HoA | 2007-10-16 14:19:52 |
 Első kérdés : (ld. BohnerGézáé) Az ABC síkra merőleges vetítésre gondolsz?
Második kérdés: AZ ABC síkban fekvő, B-nél derékszögű ABC*  C* csúcsát keresed, ahol BC* = 10 egység? C* csúcsát keresed, ahol BC* = 10 egység?
|
| Előzmény: [899] farkasb, 2007-10-16 12:06:35 |
|
| [900] BohnerGéza | 2007-10-16 14:12:04 |
 Nem érthető (számomra) a feladat! Azt a részt, hogy egy pont legyen merőleges egy szakaszra, azt valószínűleg más sem érti.
Az elején merőleges vetítés van?
Fogalmazd meg jól a feladatot, talán tudunk segíteni.
|
| Előzmény: [899] farkasb, 2007-10-16 12:06:35 |
|
| [899] farkasb | 2007-10-16 12:06:35 |
 Kedves Fórumozók!
Ilyen nehezet kérdeztem (nem hinném), vagy túl egyszerű? Megköszönném, ha valaki tudna segíteni.
|
|
| [898] farkasb | 2007-10-14 23:16:22 |
 Egy újabb, elvileg egyszerű kérdésem lenne. Adott A B C pont a térben. -Hogyan határozhatom meg azt a pontot(pontokat), mely az ABC síkra vetítve a vetítősugár a B ponton menne át, és B ponttól 10 egységnyire van. -továbbá szükség lenne arra a pontra (pontokra), amelyik AB szakaszra merőleges, és a ABC síkon helyezkedik el, és B pontból indul, és 10 egységnyire van tőle. Előre is köszönet!
|
|





 -ek szögei 10o egész számú többszörösei, jól használható a szabályos 18-szög oldalaiból, átlóiból és körülírt K köréből álló H18 hálózat. Ha ívhossz egységnek K két szomszédos csúcs közötti ívét vesszük, n egységnyi ívhez n.10o kerületi és n.20o középponti szög tartozik.
-ek szögei 10o egész számú többszörösei, jól használható a szabályos 18-szög oldalaiból, átlóiból és körülírt K köréből álló H18 hálózat. Ha ívhossz egységnek K két szomszédos csúcs közötti ívét vesszük, n egységnyi ívhez n.10o kerületi és n.20o középponti szög tartozik.  =100o és P2P9P6
=100o és P2P9P6








 10.n0.
10.n0.  adatokkal. A szerkesztendő X ill. Y pontok [885] szerint. A Ka Apolloniusz-kör átmérője d=b/cos
adatokkal. A szerkesztendő X ill. Y pontok [885] szerint. A Ka Apolloniusz-kör átmérője d=b/cos
