| [937] HoA | 2007-11-16 09:26:03 |
 Lehet, hogy kicsit nehéz a felfogásom, de nekem még így sem világos. Légy szíves írd le magyarul, mi a két feladat, valahogy így:
1) Szerkesszünk háromszöget, ha adott  = = /2, ma=1 és fb=2 /2, ma=1 és fb=2
2) Szerkesszünk háromszöget, ha adott a=1,ma=1 és fb=1
|
| Előzmény: [936] Bubóka, 2007-11-16 06:59:56 |
|
| [936] Bubóka | 2007-11-16 06:59:56 |
 Egyetemi jegyzetben található, a szerkesztő általi sajátos jelölési mód (szerintem)A jobb oldalon az "a" oldal a magasság, illetve a szögfelező adatai vannak. A p- pí akar lenni, így (el lett írva) nem a oldal hanem alfa szög.
|
| Előzmény: [935] HoA, 2007-11-15 14:19:10 |
|
| [935] HoA | 2007-11-15 14:19:10 |
 Én sem tudom, mennyire egyezményesek, pedig nem akarom ide írni hány éve foglalkozom szerkesztési feladatokkal. Honnan vetted ezt a jelölést és mit jelent? A baloldalakat majdnem megmagyaráztad - ha jól sejtem az a oldal, az ma magasság és a fb szögfelező adott. De mit jelentenek a jobboldalak?
|
| Előzmény: [934] Bubóka, 2007-11-11 19:58:01 |
|
| [934] Bubóka | 2007-11-11 19:58:01 |
 Üdv Mindenkinek!
Segítséget szeretnék kérni a következő feladathoz.Nagyon fontos lenne!
Bizonyítsuk be, hogy az alábbi háromszögszerkesztési feladatok nem szerkeszthetők euklidészi értelemben! A harmadfokú problémáknál vizsgáljuk, hogy megoldható-e szögharmadoló eszközzel.
1. (a, ha, wb ) = ( p/2, 1, 2 )
2. (a, ha, wb ) = ( 1, 1, 1 )
Nem tudom mennyire egyezményesek ezek a jelek, a w - a szögfelezőt, h- a magasságot jelentené.
|
|
| [933] sakkmath | 2007-11-07 17:51:31 |
 Megoldásra ajánlom a következő feladatot.
Az R pont a K középpontú kör PQ húrjának felezéspontja. Bizonyítsuk be, hogy az ábra szerinti elrendezésben SY>RX. Elnézést, a rajz most csak ilyenre sikeredett :(
|
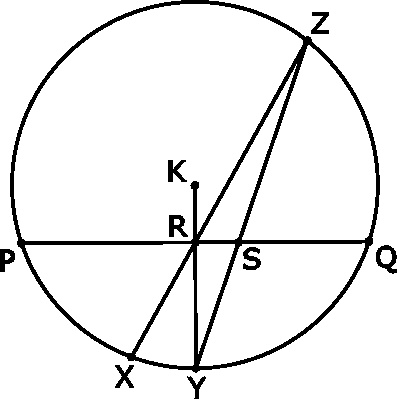 |
|
|
| [931] Fálesz Mihály | 2007-11-05 13:48:22 |
 Egyáltalán nem fitymálni akartam a mátrixos megközelítést. A gyakorlatban is mátrixokat használnak (pl. a számítógépes grafikában).
* * *
Nézzük meg inkább a kvaterniós megoldást.
Legyen u egy egységvektor,  egy szög és egy szög és
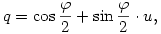
tehát q az a kvaternió, aminek skalár része 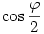 , vektor része pedig , vektor része pedig 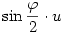 . Nézzük meg, mit csinál a következő leképezés: . Nézzük meg, mit csinál a következő leképezés:
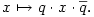
Az x kvaterniót felírhatjuk a+bu+v alakban, ahol a,b skalárok, v pedig egy u-ra merőleges vektor. Legyen w=u×v a v elforgatottja u körül derékszöggel; némi számolás után kijön, hogy
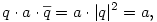
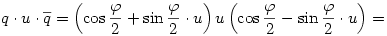
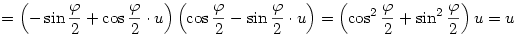
és
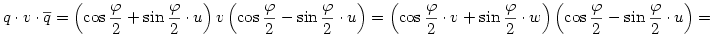
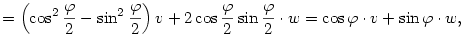
tehát
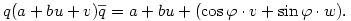
A skalár rész és az u-val párhuzamos vektor komponens nem változik, az u-ra merőleges vektor komponens pedig elfordul  szöggel. Vagyis a művelet elforgatja a vektor részt u körül szöggel. Vagyis a művelet elforgatja a vektor részt u körül  szöggel. szöggel.
|
| Előzmény: [928] BohnerGéza, 2007-11-05 01:57:56 |
|
|
|
| [928] BohnerGéza | 2007-11-05 01:57:56 |
 Beismerem, a kvaterniókkal nem foglalkoztam, csak a síkbeliekkel, azaz a komplex számokkal. (remélem nem tévedek)
Az előző hozzászólásomban leírtak a komplex számok segítségével történő forgatásnál is kellenek (eltolás - forgatás - visszatolás) kivonás - szorzás - visszaadás alakban. Talán szebb, de a számítógép számára ugyanannyi lépés.
A sik összes egyenes és osztóviszony tartó leképezése megadható olyan speciális mátrixszal, melynek utolsó sora 0,0,1, (utolsó oszlopa pedig az origó képe és az 1-es.) azaz hat paramétert kell meghatározni. Az (x;y) képét a mátrixot az (x;y;1) oszlopvektorral szorozva kapjuk. Ez 4 szorzást és 6 összeadást jelent. (Térben 9 szorzás és 12 összeadás.)
|
| Előzmény: [927] Fálesz Mihály, 2007-11-04 23:07:02 |
|
|
| [926] BohnerGéza | 2007-11-04 22:46:22 |
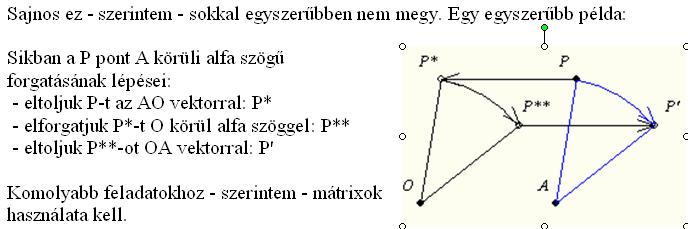
 Az O-t helybenhagyó leképezések egyszerűbbek, ezért ilyen az általános módszer.
Egy-egy speciális eset lehet egyszerűbb, de mindenképpen ajánlom az általánossal való foglalkozást.
|
 |
| Előzmény: [925] farkasb, 2007-11-04 21:31:19 |
|
| [925] farkasb | 2007-11-04 21:31:19 |
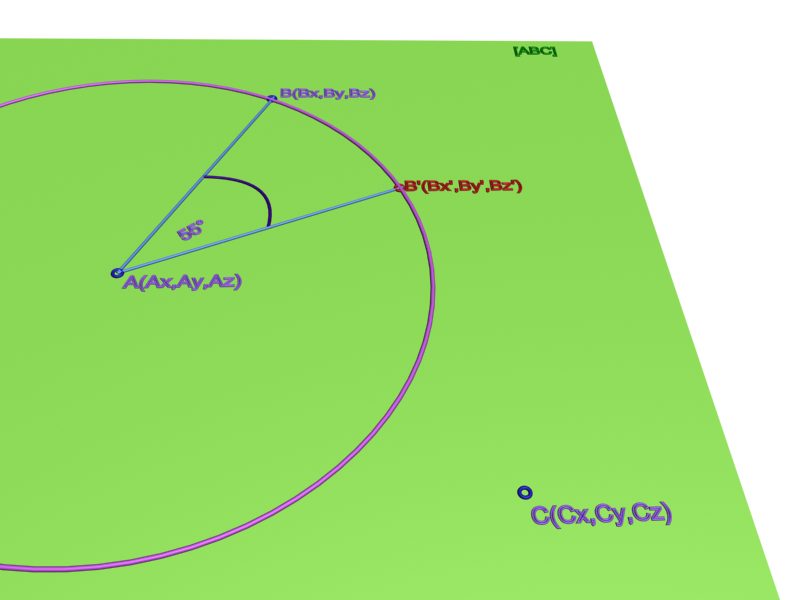
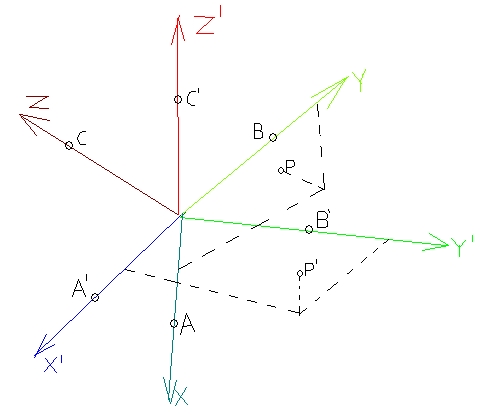
 Lehet, hogy félreértettük egymást, vagy csak számomra tűnik túl bonyolultnak a megoldás, ezért a félreértés elkerülése végett feltöltök egy ábrát. Lényegében a Keresett B' pont rajta van a síkon, és az AB köríven, és mondjuk AB szakasztól 55 fokkal van elforgatva.
|
 |
| Előzmény: [923] BohnerGéza, 2007-11-02 04:49:24 |
|
| [924] Bubóka | 2007-11-02 13:02:27 |
 Tisztelt Fórumozók!
Segítségeteket kérném! A napokban hallottam a geogebráról. Valaki küldjön már nekem legyen szíves egy feladatot (ami esetleg egy nyomvonalat is tartalmaz) és annak megoldását, amit a geogebrával készített el.
Köszi!
|
|
|
| [922] farkasb | 2007-11-01 10:52:36 |
 Kedves Fórumozók!
Ismételten segítségre szorulok. Adott ABC pont xyz koordinátákkal, ami meghatároz egy síkot. A pont körül hogyan tudom a síkban elforgatni B-t egy tetszőleges szöggel?
|
|
|
|
| [919] Cckek | 2007-10-25 23:02:49 |
 Köszönöm mindkettőtöknek, HoA és Bohner Géza ezeket az érdekes hozzászolásokat, nekem is van egy "csúnya" trigonometrikus megoldásom, de ez nem vetekszik egyikötök megoldásával sem. Köszi.
|
|
| [918] farkasb | 2007-10-25 22:59:45 |
 Kedves Fórumozók!
Lenne egy újabb kérdésem/problémám.
Térbeli koordináta transzformációl lenne szó.
Adott két derékszögű koordináta rendszer, és egy P pont.
Az eredeti koordináta rendszer origója (0,0,0)
X tengelyén A (29.955,2,556,-39,952) //50 egységre O-tól
Y tengelyén B (10.063,47,815,10,604) //50 egységre O-tól
Z tengelyén C (38.748,-14.393,28.132) //50 egységre O-tól
P(20.653,53.039,4,877)
A cél koordináta rendszer origója szintén (0,0,0)
X tengelyén A' (50,0,0)
Y tengelyén B' (0,50,0)
Z tengelyén C' (0,0,50)
Keresett a P pont cél koordináta rendszer beli x,y,z koordinátája.
3dStudio Max porgrammal csináltam meg fordítva az egészet, és a keresett P' pont koordinátái: (10,30,15)
Próbáltam kiszámolni ezt a forgatást, de sehogy sem jött össze. Ezért kérnék némi segítséget.
Ezeket a képleteket használtam:
r11= cos(gamma)*cos(béta)
r12= cos(gamma)*sin(béta)*sin(alfa)-sin(gamma)*cos(alfa)
r13= cos(gamma)*sin(béta)*cos(alfa)+sin(gamma)*sin(alfa)
r21= sin(gamma)*cos(béta)
r22= sin(gamma)*sin(béta)*sin(alfa)+cos(gamma)*cos(alfa)
r23= sin(gamma)*sin(gamma)*sin(béta)*cos(alfa)-cos(gamma)*sin(alfa)
r31= -sin(béta)
r32= cos(béta)*sin(alfa)
r33= cos(béta)*cos(alfa)
P'x= r11* Px+ r12* Py+ r13* Pz
P'y= r21* Px+ r22* Py+ r23* Pz
P'z= r31* Px+ r32* Py+ r33* Pz
Előre is köszönöm a segítséget!
|
|
| [917] HoA | 2007-10-25 19:19:39 |
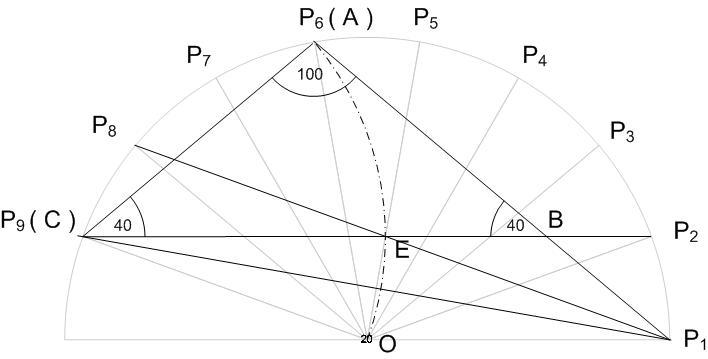
 A KöMaL régebbi olvasói számára ismert, hogy az ilyen feladatok megoldásához, ahol a  -ek szögei 10o egész számú többszörösei, jól használható a szabályos 18-szög oldalaiból, átlóiból és körülírt K köréből álló H18 hálózat. Ha ívhossz egységnek K két szomszédos csúcs közötti ívét vesszük, n egységnyi ívhez n.10o kerületi és n.20o középponti szög tartozik. -ek szögei 10o egész számú többszörösei, jól használható a szabályos 18-szög oldalaiból, átlóiból és körülírt K köréből álló H18 hálózat. Ha ívhossz egységnek K két szomszédos csúcs közötti ívét vesszük, n egységnyi ívhez n.10o kerületi és n.20o középponti szög tartozik.
Legyenek H18 csúcsai P1,.., P18, K középpontja O, sugara R. Húzzuk be a P1P6, P2P9 és P6P9 átlókat. Legyen A=P6,C=P9 , B pedig P1P6 és P2P9 metszéspontja. Ekkor ABC a feladatban szereplő  , hiszen P1P6P9 , hiszen P1P6P9 =100o és P2P9P6 =100o és P2P9P6 =40o. =40o.
OP6P9 R oldalú szabályos  . Legyen a C középpontú R sugarú kör és a BC szakasz metszéspontja E. Ekkor BE a feladatban szereplő oldalhossz különbség. OCE egyenlőszárú . Legyen a C középpontú R sugarú kör és a BC szakasz metszéspontja E. Ekkor BE a feladatban szereplő oldalhossz különbség. OCE egyenlőszárú  csúcsszöge 60o-40o=20o, COE csúcsszöge 60o-40o=20o, COE =80o , E rajta van az OP5 sugáron. De akkor E a P2P9 átló e sugárra vett tükörképén, P1P8 -on is rajta van. A BP1E =80o , E rajta van az OP5 sugáron. De akkor E a P2P9 átló e sugárra vett tükörképén, P1P8 -on is rajta van. A BP1E -ben BP1E -ben BP1E =P6P1P8 =P6P1P8 =20o, a B-nél lévő külső szög 40o, P1BE =20o, a B-nél lévő külső szög 40o, P1BE egyenlőszárú, így P1 feladatunk D pontja. ADC egyenlőszárú, így P1 feladatunk D pontja. ADC =P6P1P9 =P6P1P9 =30o. =30o.
|
 |
| Előzmény: [910] Cckek, 2007-10-21 07:31:36 |
|
|
|
| [914] Draskóczy Gergely | 2007-10-24 16:30:12 |
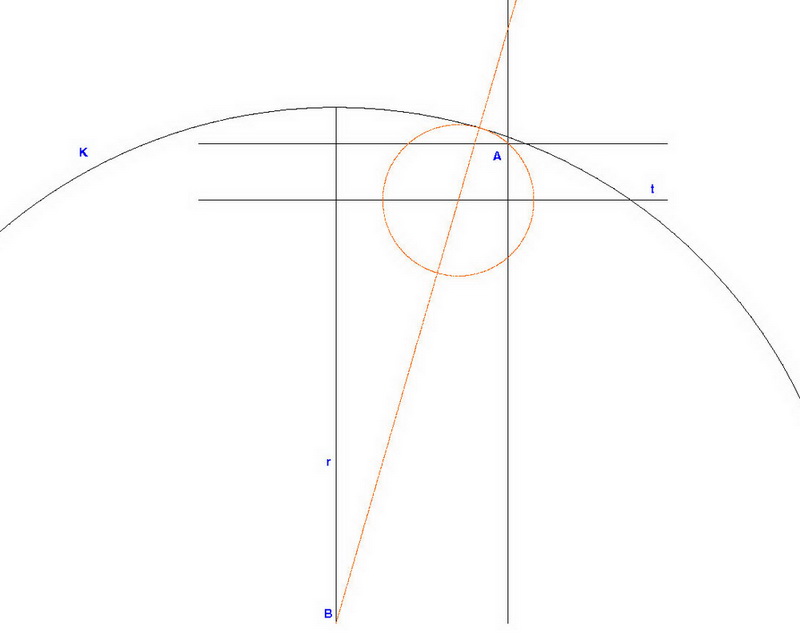
 Munkám során merült föl az alábbi probléma:
adott A pont, K kör, t egyenes
szerkesszünk geometriai úton olyan kört (2 is van) mely átmegy A ponton, középpontja t egyenesen van, érinti a K kört
Tud ebben valaki segíteni?
Gergő
|
 |
|
|



 =
= /2, ma=1 és fb=2
/2, ma=1 és fb=2 

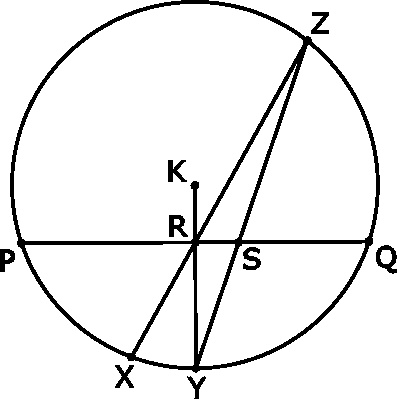

 egy szög és
egy szög és 




 -ek szögei 10o egész számú többszörösei, jól használható a szabályos 18-szög oldalaiból, átlóiból és körülírt K köréből álló H18 hálózat. Ha ívhossz egységnek K két szomszédos csúcs közötti ívét vesszük, n egységnyi ívhez n.10o kerületi és n.20o középponti szög tartozik.
-ek szögei 10o egész számú többszörösei, jól használható a szabályos 18-szög oldalaiból, átlóiból és körülírt K köréből álló H18 hálózat. Ha ívhossz egységnek K két szomszédos csúcs közötti ívét vesszük, n egységnyi ívhez n.10o kerületi és n.20o középponti szög tartozik.  =100o és P2P9P6
=100o és P2P9P6


