|
| [945] Python | 2007-11-25 12:32:17 |
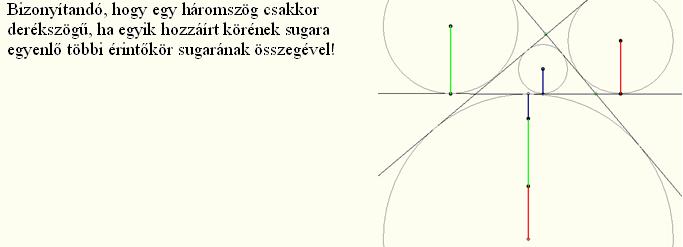
 Legyenek a háromszög oldalai a, b, c, beírt körésnek sugara r, a hozzáírt körök sugara ra, rb, rc (pl. ra az a oldalhoz írt kör) ! Tegyük fel hogy pl. rc=r+ra+rb! Felhasználva hogy a t háromszögterületre 2t=r(a+b+c)=ra(-a+b+c)=rb(a-b+c)=rc(a+b-c)
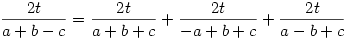
A nevezők a háromszög-egyenlőtlenség miatt pozitívak, felszorozva; 2t-vel osztva
![(a+b+c)\left[(a-b+c)(-a+b+c)+(a+b+c)(a-b+c+-a+b+c)\right]=](keplet.cgi?k=99215EE03C84BB72)
=(a+b+c)(a-b+c)(-a+b+c)
Elvégezve a műveleteket
4c(c2-b2-a2)=0
Itt 4c 0, így c2=a2+b2, és ekkor a Pithagorasz-tétel megfordítása miatt a háromszög derékszögű. 0, így c2=a2+b2, és ekkor a Pithagorasz-tétel megfordítása miatt a háromszög derékszögű.
|
| Előzmény: [943] BohnerGéza, 2007-11-22 18:21:24 |
|
|
|
|
|
| [940] HoA | 2007-11-16 16:20:18 |
 OK, helyesbítek. Tegyük fel, az adatok most már világosak. A feladat tehát így szól
1) "Bizonyítsuk be, hogy nem szerkeszthető meg a hármszög, ha adott  = = /2, ma=1 és fb=2" , illetve /2, ma=1 és fb=2" , illetve
2) "Bizonyítsuk be, hogy nem szerkeszthető meg a hármszög, ha adott a=1 , ma=1 és fb=1"
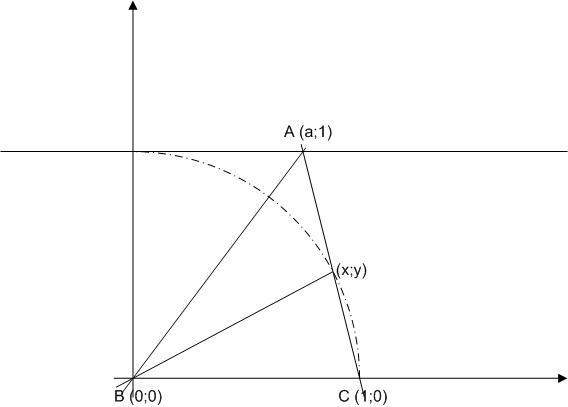
Ha így van, akkor 2) megoldásának egyik lehetséges módja: Az ábra szerint az A csúcs x koordinátájával (a) fejezzük ki x-et és y-t annak alapján, hogy
x2+y2=1 és 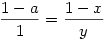
Ha jól számoltam, 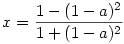 Ezután felírjuk, hogy a felezett szöggel szemközti oldalnak a szögfelező által elvágott két darabja - és így ezek x irányú vetületei is - úgy aránylanak, mint a közrezáró oldalak hossza: Ezután felírjuk, hogy a felezett szöggel szemközti oldalnak a szögfelező által elvágott két darabja - és így ezek x irányú vetületei is - úgy aránylanak, mint a közrezáró oldalak hossza:
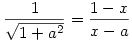 , persze x-et a-val kifejezve, kapunk a-ra egy magasabbfokú egyenletet. Erről kell (lehet?) megmutatni, hogy a megoldás nincs benne az adott adatokból szerkesztéssel elérhető számtestben. , persze x-et a-val kifejezve, kapunk a-ra egy magasabbfokú egyenletet. Erről kell (lehet?) megmutatni, hogy a megoldás nincs benne az adott adatokból szerkesztéssel elérhető számtestben.
|
 |
| Előzmény: [938] Bubóka, 2007-11-16 14:03:32 |
|
|
| [938] Bubóka | 2007-11-16 14:03:32 |
 Valószínű nem a felfogásoddal van baj! A feladat az, az amit leírtam a 935 alatt, de sajna csak ennyi:
Bizonyítsuk be, hogy az alábbi háromszögszerkesztési feladatok nem szerkeszthetők euklidészi értelemben! A harmadfokú problémáknál vizsgáljuk, hogy megoldható-e szögharmadoló eszközzel. .... és az adatok.
Nem szerkesztésről van szó. Bocsánat, de nem tudok itt egyszerű szövegen kívűl mást "szerkeszteni", ha pedig vágólapról akarok másolni, akkor nem másolja ugyanazt.
|
| Előzmény: [937] HoA, 2007-11-16 09:26:03 |
|
| [937] HoA | 2007-11-16 09:26:03 |
 Lehet, hogy kicsit nehéz a felfogásom, de nekem még így sem világos. Légy szíves írd le magyarul, mi a két feladat, valahogy így:
1) Szerkesszünk háromszöget, ha adott  = = /2, ma=1 és fb=2 /2, ma=1 és fb=2
2) Szerkesszünk háromszöget, ha adott a=1,ma=1 és fb=1
|
| Előzmény: [936] Bubóka, 2007-11-16 06:59:56 |
|
| [936] Bubóka | 2007-11-16 06:59:56 |
 Egyetemi jegyzetben található, a szerkesztő általi sajátos jelölési mód (szerintem)A jobb oldalon az "a" oldal a magasság, illetve a szögfelező adatai vannak. A p- pí akar lenni, így (el lett írva) nem a oldal hanem alfa szög.
|
| Előzmény: [935] HoA, 2007-11-15 14:19:10 |
|
| [935] HoA | 2007-11-15 14:19:10 |
 Én sem tudom, mennyire egyezményesek, pedig nem akarom ide írni hány éve foglalkozom szerkesztési feladatokkal. Honnan vetted ezt a jelölést és mit jelent? A baloldalakat majdnem megmagyaráztad - ha jól sejtem az a oldal, az ma magasság és a fb szögfelező adott. De mit jelentenek a jobboldalak?
|
| Előzmény: [934] Bubóka, 2007-11-11 19:58:01 |
|
| [934] Bubóka | 2007-11-11 19:58:01 |
 Üdv Mindenkinek!
Segítséget szeretnék kérni a következő feladathoz.Nagyon fontos lenne!
Bizonyítsuk be, hogy az alábbi háromszögszerkesztési feladatok nem szerkeszthetők euklidészi értelemben! A harmadfokú problémáknál vizsgáljuk, hogy megoldható-e szögharmadoló eszközzel.
1. (a, ha, wb ) = ( p/2, 1, 2 )
2. (a, ha, wb ) = ( 1, 1, 1 )
Nem tudom mennyire egyezményesek ezek a jelek, a w - a szögfelezőt, h- a magasságot jelentené.
|
|
| [933] sakkmath | 2007-11-07 17:51:31 |
 Megoldásra ajánlom a következő feladatot.
Az R pont a K középpontú kör PQ húrjának felezéspontja. Bizonyítsuk be, hogy az ábra szerinti elrendezésben SY>RX. Elnézést, a rajz most csak ilyenre sikeredett :(
|
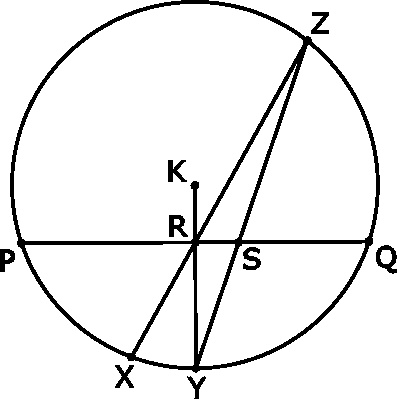 |
|
|
| [931] Fálesz Mihály | 2007-11-05 13:48:22 |
 Egyáltalán nem fitymálni akartam a mátrixos megközelítést. A gyakorlatban is mátrixokat használnak (pl. a számítógépes grafikában).
* * *
Nézzük meg inkább a kvaterniós megoldást.
Legyen u egy egységvektor,  egy szög és egy szög és
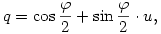
tehát q az a kvaternió, aminek skalár része 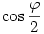 , vektor része pedig , vektor része pedig 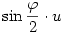 . Nézzük meg, mit csinál a következő leképezés: . Nézzük meg, mit csinál a következő leképezés:
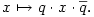
Az x kvaterniót felírhatjuk a+bu+v alakban, ahol a,b skalárok, v pedig egy u-ra merőleges vektor. Legyen w=u×v a v elforgatottja u körül derékszöggel; némi számolás után kijön, hogy
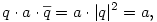
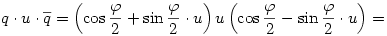
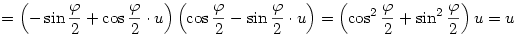
és
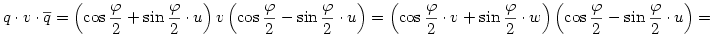
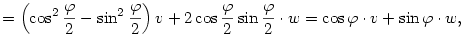
tehát
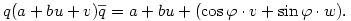
A skalár rész és az u-val párhuzamos vektor komponens nem változik, az u-ra merőleges vektor komponens pedig elfordul  szöggel. Vagyis a művelet elforgatja a vektor részt u körül szöggel. Vagyis a művelet elforgatja a vektor részt u körül  szöggel. szöggel.
|
| Előzmény: [928] BohnerGéza, 2007-11-05 01:57:56 |
|
|
|
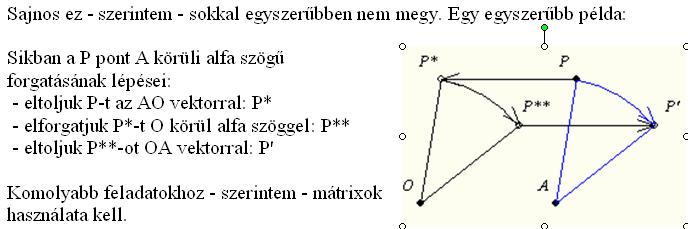
| [928] BohnerGéza | 2007-11-05 01:57:56 |
 Beismerem, a kvaterniókkal nem foglalkoztam, csak a síkbeliekkel, azaz a komplex számokkal. (remélem nem tévedek)
Az előző hozzászólásomban leírtak a komplex számok segítségével történő forgatásnál is kellenek (eltolás - forgatás - visszatolás) kivonás - szorzás - visszaadás alakban. Talán szebb, de a számítógép számára ugyanannyi lépés.
A sik összes egyenes és osztóviszony tartó leképezése megadható olyan speciális mátrixszal, melynek utolsó sora 0,0,1, (utolsó oszlopa pedig az origó képe és az 1-es.) azaz hat paramétert kell meghatározni. Az (x;y) képét a mátrixot az (x;y;1) oszlopvektorral szorozva kapjuk. Ez 4 szorzást és 6 összeadást jelent. (Térben 9 szorzás és 12 összeadás.)
|
| Előzmény: [927] Fálesz Mihály, 2007-11-04 23:07:02 |
|
|
| [926] BohnerGéza | 2007-11-04 22:46:22 |
 Az O-t helybenhagyó leképezések egyszerűbbek, ezért ilyen az általános módszer.
Egy-egy speciális eset lehet egyszerűbb, de mindenképpen ajánlom az általánossal való foglalkozást.
|
 |
| Előzmény: [925] farkasb, 2007-11-04 21:31:19 |
|
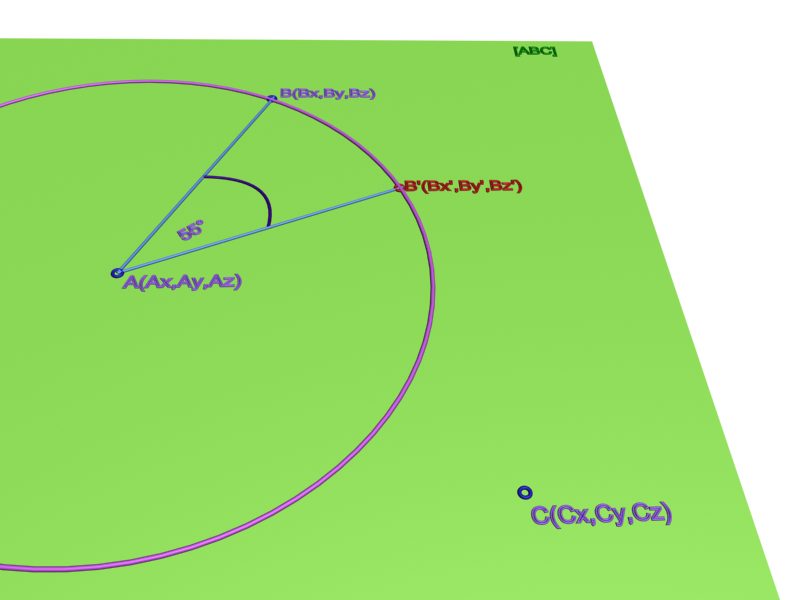
| [925] farkasb | 2007-11-04 21:31:19 |
 Lehet, hogy félreértettük egymást, vagy csak számomra tűnik túl bonyolultnak a megoldás, ezért a félreértés elkerülése végett feltöltök egy ábrát. Lényegében a Keresett B' pont rajta van a síkon, és az AB köríven, és mondjuk AB szakasztól 55 fokkal van elforgatva.
|
 |
| Előzmény: [923] BohnerGéza, 2007-11-02 04:49:24 |
|
| [924] Bubóka | 2007-11-02 13:02:27 |
 Tisztelt Fórumozók!
Segítségeteket kérném! A napokban hallottam a geogebráról. Valaki küldjön már nekem legyen szíves egy feladatot (ami esetleg egy nyomvonalat is tartalmaz) és annak megoldását, amit a geogebrával készített el.
Köszi!
|
|
|
| [922] farkasb | 2007-11-01 10:52:36 |
 Kedves Fórumozók!
Ismételten segítségre szorulok. Adott ABC pont xyz koordinátákkal, ami meghatároz egy síkot. A pont körül hogyan tudom a síkban elforgatni B-t egy tetszőleges szöggel?
|
|



 =s-c;
=s-c;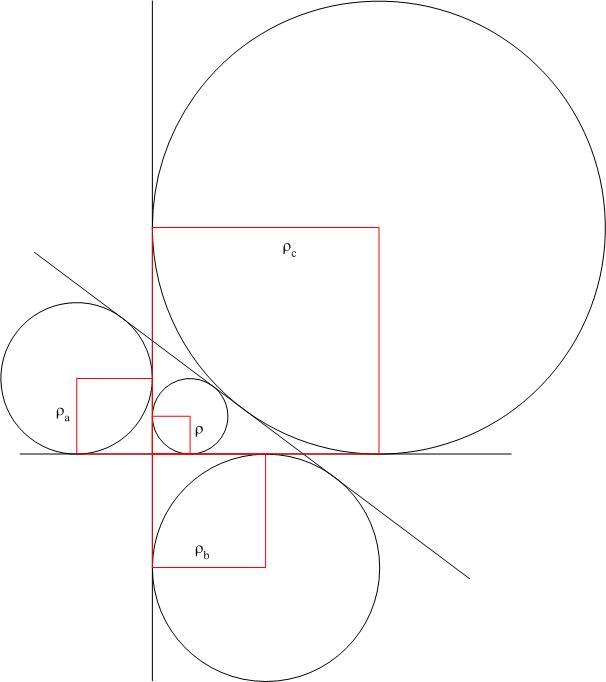

 0, így c2=a2+b2, és ekkor a Pithagorasz-tétel megfordítása miatt a háromszög derékszögű.
0, így c2=a2+b2, és ekkor a Pithagorasz-tétel megfordítása miatt a háromszög derékszögű.
 hegyesszög. Határozzuk meg azon ABC háromszögek körülírt körének középpontjainak halmazát, melyek A csúcsánál az
hegyesszög. Határozzuk meg azon ABC háromszögek körülírt körének középpontjainak halmazát, melyek A csúcsánál az 

 /2, ma=1 és fb=2" , illetve
/2, ma=1 és fb=2" , illetve 


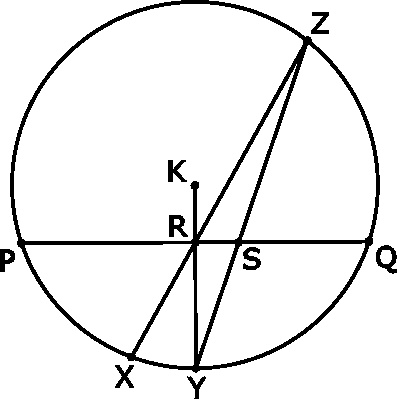

 egy szög és
egy szög és 

