|
| [623] HOMI | 2004-11-25 02:24:03 |
 A g(x) injektiv,mert ha g(a)=g(b) akkor 1/a=g(g(a))=g(g(b))=1/b,azaz a=b.Az 1/x mindent felvesz (0,+végtelen)-en,igy g(g(x)) szürjektiv,azaz g(x) is szürjektiv.A g(x) folytonos,injektiv,szürjektiv tehát szigorúan monoton.Ha g(x) szig.mon.növekedne,g(g(x)) is azt tenné de 1/x szig.mon csökken.Igy g szig mon csökken és a felvett értékkészlete a teljes(0,+végtelen).Ekkor ha x 'kicsi', g(x) 'nagy',g(g(x)) 'kicsi' ,de 1/x 'nagy'.Ez ellentmondás,mert g(g(x)))=1/x.(A fentiek pontos megfogalmazása: ha x tart 0-hoz g(x)->+végtelen,igy g(g(x))->0,de 1/x->végtelen).
|
| Előzmény: [622] jenei.attila, 2004-11-24 20:39:06 |
|
| [622] jenei.attila | 2004-11-24 20:39:06 |
 Egy nem túl nehéz, de szerintem érdekes feladat:
Bizonyítsuk be, hogy nincs olyan g:R+ R+ folytonos függvény, amelyre g(g(x))=1/x minden x R+ folytonos függvény, amelyre g(g(x))=1/x minden x R+-ra. R+-ra.
|
|
|
| [620] rizs | 2004-11-24 19:14:02 |
 Ha már Fibonacci a téma, akkor ezt ajánlom még egyszer :) 118.: Ha a Fibonacci sorozat elemeit egy-egy tizedeshellyel eltolva (akár balról jobbra, akár jobbról balra haladva) egymás alá írjuk és összeadjuk, akkor a sok szám összege végül ismétlődő szakaszokból fog állni, tehát olyan lesz, mint a végtelen szakaszos tizedestörtek. Sőt, nem csak olyan, hanem az is! Ha megfelelő helyre tesszük a tizedesvesszőt, akkor a két összeg éppen 1/A, illetve 1/B értékű lesz, ahol A és B prímszámok. Mennyi A és B?
|
|
| [619] Maga Péter | 2004-11-24 18:45:38 |
 A hatványsoros megoldáshoz hozzátenném, hogy az összes ilyen tulajdonságú függvényt generálja. Tehát: az ex hatványsorából érdemes indulni, ez 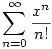 . Ezek után pedig a minden 0 és 7 közötti egész i-re a 8k+i alakú egészekhez tartozó együtthatókat ugyanazzal a ci konstanssal szorozni. A tagok elhagyása (amit szefoharcos írt) a ci=0. Csak arra kell figyelni, hogy ha ügyetlenül választjuk meg ezeket a konstansokat, akkor korábbi derivált is lehet az eredeti függvény. Ez akkor teljesül, ha ugyanazt a kostans szorzót (ci) választjuk olyan együtthatókhoz, amelyeknek különbsége 8-nál kisebb, a 8-hoz nem relatív prím. A felírt hatványsor mindig értelmes, ezt a Cauchy-Hadamaard kritériummal lehet ellenőrizni. . Ezek után pedig a minden 0 és 7 közötti egész i-re a 8k+i alakú egészekhez tartozó együtthatókat ugyanazzal a ci konstanssal szorozni. A tagok elhagyása (amit szefoharcos írt) a ci=0. Csak arra kell figyelni, hogy ha ügyetlenül választjuk meg ezeket a konstansokat, akkor korábbi derivált is lehet az eredeti függvény. Ez akkor teljesül, ha ugyanazt a kostans szorzót (ci) választjuk olyan együtthatókhoz, amelyeknek különbsége 8-nál kisebb, a 8-hoz nem relatív prím. A felírt hatványsor mindig értelmes, ezt a Cauchy-Hadamaard kritériummal lehet ellenőrizni.
|
| Előzmény: [618] Lóczi Lajos, 2004-11-24 18:20:46 |
|
| [618] Lóczi Lajos | 2004-11-24 18:20:46 |
 Valóban, amely Általad említett függvény a koszinusz-analógiával is felírható persze:
legyen ismét  egy primitív nyolcadik egységgyök, ekkor egy primitív nyolcadik egységgyök, ekkor
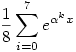
lesz az a valós függvény, amely ex hatványsorából úgy keletkezik, hogy csak minden 8. tagot hagyunk meg, azaz a fenti függvény 0 körüli hatványsorának eleje
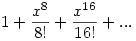
Egyébként ez csak valós elemi függvényekkel kifejezve egy harmadik alakban így fest:
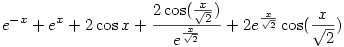
vagy, ha a ch koszinusz-hiperbolikusz függvényt is használhatom, akár így:
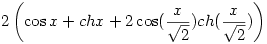
|
| Előzmény: [617] szefoharcos, 2004-11-24 17:43:32 |
|
| [617] szefoharcos | 2004-11-24 17:43:32 |
 Kedves Lajos!
Gratulaalok a megoldaasaidhoz! A Fibonacci-szaamokra ugyanezt talaaltam een is, de a fuggveenyesre volna egy megjegyzeesem, ami nem toolem szaarmazik: hatvaanysorok... Ahogy Kemeeny Legeeny is megoldotta, mieloott hangneme miatt letiltottaak volna: Az xn/n! sor minden 8. tagjaat hagyjuk csak meg. Konnyuu ellenoorizni, hogy ez joo.
|
|
| [616] Lóczi Lajos | 2004-11-24 15:03:36 |
 Egy kis segítség a 121. feladathoz:
némi keresgélés után rájöttem, hogy
F2n+1=Fn+12+Fn2 illetve
F2n=Fn+12-Fn-12,
ahol n pozitív természetes szám és Fn az n-edik Fibonacci szám, ha a sorozat így kezdődik: F1=1, F2=1, F3=2, stb.
Ezeket már könnyű bizonyítani például a Fibonacci-számok explicit alakjából.
|
| Előzmény: [604] szefoharcos, 2004-11-23 22:42:38 |
|
|
| [614] Lóczi Lajos | 2004-11-24 12:54:56 |
 Nyilván nem, csak ez az egy ilyen hármasiker van. Hiszen ha az első tag 3-nál nagyobb prím, akkor 3-mal maradékosan osztva 1-et vagy 2-t ad. De ekkor az első esetben a sorozat 2. tagja 3-mal osztható lenne, míg a második esetben a sorozat 3. tagja volna 3-mal osztható.
|
| Előzmény: [612] Hajba Károly, 2004-11-24 12:48:27 |
|
|
| [612] Hajba Károly | 2004-11-24 12:48:27 |
 Hamár így belemelegedett a topiktagság a prímek keresésébe, nekem is lenne egy érdekes kérdésem. Létezik-e a 3, 5, 7 számhármason kívül még hármasiker prímszámhármas, azaz a prímek olyan 3 tagú sorozata, mely diferenciája 2? Habár ez már talán a számelmélet topikba illene. :o)
HK
|
|
|
| [610] Lóczi Lajos | 2004-11-24 12:20:37 |
 100000-ig az összes ilyen prímnégyes egyébként rendre:
251, 257, 263, 269
1741, 1747, 1753, 1759
3301, 3307, 3313, 3319
5101, 5107, 5113, 5119
5381, 5387, 5393, 5399
6311, 6317, 6323, 6329
6361, 6367, 6373, 6379
12641, 12647, 12653, 12659
13451, 13457, 13463, 13469
14741, 14747, 14753, 14759
15791, 15797, 15803, 15809
15901, 15907, 15913, 15919
17471, 17477, 17483, 17489
18211, 18217, 18223, 18229
19471, 19477, 19483, 19489
23321, 23327, 23333, 23339
26171, 26177, 26183, 26189
30091, 30097, 30103, 30109
30631, 30637, 30643, 30649
53611, 53617, 53623, 53629
56081, 56087, 56093, 56099
62201, 62207, 62213, 62219
63691, 63697, 63703, 63709
71341, 71347, 71353, 71359
74453, 74471, 74489, 74507 -- ha jól látom, ez az első, ahol nem 6 a differencia
75521, 75527, 75533, 75539
76543, 76561, 76579, 76597 -- itt sem
77551, 77557, 77563, 77569
78791, 78797, 78803, 78809
80911, 80917, 80923, 80929
82781, 82787, 82793, 82799
83431, 83437, 83443, 83449
84431, 84437, 84443, 84449
89101, 89107, 89113, 89119
89381, 89387, 89393, 89399
91291, 91297, 91303, 91309
94421, 94427, 94433, 94439
95261, 95267, 95273, 95279
95911, 95917, 95923, 95929
104711, 104717, 104723, 104729
stb.
|
| Előzmény: [603] rizs, 2004-11-23 20:11:36 |
|
| [604] szefoharcos | 2004-11-23 22:42:38 |
 Csá, mindenki!
Nem TaGlalnám, hogy a következő problémák miért "érdekesek":)... Szóval:
120. Van-e olyan függvény, aminek nyolcadik deriváltja önmaga, de semelyik korábbi sem?
121. Bizonyítsuk be, hogy minden Fibonacci-szám felírható két négyzetszám különbsége vagy összegeként!
Jó elmélkedést! Pá!
|
|
| [603] rizs | 2004-11-23 20:11:36 |
 Köszi Csimby és Sirpi!
Gondoltam én is a programozásra, de az az egy baj, hogy tök süti vagyok :) hozzá. Így maradt a favágó módszer, azaz prímszám-táblákkal való szemezgetés, de ezt a megoldást így valahogy nem láttam meg.
Még egyszer köhi hépen!
És még egy kérdés: A börtönös feladatnak a kapcsolók ismeretlen kezdeti állásának esetére nincs valami ötletetek?
|
|
| [602] Csimby | 2004-11-23 16:05:44 |
 Egyébként 32000-ig csak olyan sorozatokat találtam amelyekben a differencia 6. Ha úgy keressük a prímeket, hogy feltesszük, a differencia: 6, akkor p1, p2, p3, p4 4 különböző maradékot ad 5-tel osztva (hiszen 6  1 mod 5), de mivel mindegyik prím, ezért p1-nek 1 maradékot kell 5-tel osztva adnia. Ekkor p1 6-ra vagy 1-re végződik, 6-ost ki zárhatjuk, mert p1 páratlan kell, hogy legyen. 1 mod 5), de mivel mindegyik prím, ezért p1-nek 1 maradékot kell 5-tel osztva adnia. Ekkor p1 6-ra vagy 1-re végződik, 6-ost ki zárhatjuk, mert p1 páratlan kell, hogy legyen.
|
| Előzmény: [601] Csimby, 2004-11-23 15:41:41 |
|
|
| [600] Sirpi | 2004-11-23 15:20:40 |
 Hát, így jár, aki nem olvassa vissza a feladatot, hanem emlékezetből próbálja megoldani... Ha nem számít csalásnak, akkor erre a problémára össze lehet egy egyszerű programot dobni.
|
| Előzmény: [599] rizs, 2004-11-23 15:13:57 |
|
| [599] rizs | 2004-11-23 15:13:57 |
 Kedves Sirpi!
Bocs, elrontottam a feladat szövegét :( Szal 4 olyan egymást követő prím kell, amelyek számtani sorozatot alkotnak. Tehát a prímek között nincsen más prím! Bár ez mégis benne volt a feladatban asszem :S Szal ezé nem jó az 5, 11, 17, 23, mert 5 és 11 között ott van a 7.
|
| Előzmény: [598] Sirpi, 2004-11-23 14:31:17 |
|
| [598] Sirpi | 2004-11-23 14:31:17 |
 Ha jól értem, Neked az a 4 legkisebb pozitív prím kell, melyek nem nulla differenciájú számtani sorozatot alkotnak. Felmerül a kérdés, hogy milyen mérték szerint legkisebb, lehet pl. összegben, legnagyobb tagban, de szerintem bárhogy is nézzük, a legkisebb ilyen számnégyes az 5, 11, 17, 23.
A differencia osztható kell, hogy legyen 2-vel, ellenkező esetben két páros tagja is lenne a számtani sorozatnak, és nem lehet mindkettő a 2. A differencia hárommal is osztható kell, hogy legyen, mindenképp lesz hárommal osztható tag, és ha az nem az első tag, akkor a negyedik is hárommal osztható lesz (szóba jöhetne még, hogy a 2. tag épp 3, de akkor az elsőnek 2-nek kéne lennie, ami nem jó). Vagyis a differencia 6-tal is osztható kell legyen.
1 7 13 19
2 8 14 20
3 9 15 21
4 10 16 22
5 11 17 23
Látható, hogy amit fentebb írtam, az a legelső jó (vagyis az 5-tel kezdődő), a többiben van olyan tag is, ami nem prím.
|
| Előzmény: [597] rizs, 2004-11-23 14:03:01 |
|
| [597] rizs | 2004-11-23 14:03:01 |
 Nagyon szépen kérlek Titeket, segítsetek!
Ha valaki esetleg meg tudná oldani a legkisebb 4 egymást követő, számtani sorozatot alkotó prímes feladatot, akkor nagyon hálás lennék :) Help me.
|
|
|
| [595] Csimby | 2004-11-21 23:17:59 |
 119.feladat
Adjunk meg olyan egész együtthatós polinómot amelynek gyöke:
a. feladat: 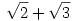
b. feladat: 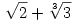
|
|
| [594] rizs | 2004-11-20 01:48:25 |
 és egy meglepő probléma:
118.: Ha a Fibonacci sorozat elemeit egy-egy tizedeshellyel eltolva (akár balról jobbra, akár jobbról balra haladva) egymás alá írjuk és összeadjuk, akkor a sok szám összege végül ismétlődő szakaszokból fog állni, tehát olyan lesz, mint a végtelen szakaszos tizedestörtek. Sőt, nem csak olyan, hanem az is! Ha megfelelő helyre tesszük a tizedesvesszőt, akkor a két összeg éppen 1/A, illetve 1/B értékű lesz, ahol A és B prímszámok. Mennyi A és B?
|
|
| [593] rizs | 2004-11-20 01:44:47 |
 ez is lehet h volt :D
117. feladat:
N embert sorbaállítanak. (Az i-dik látja 1-től (i-1)-ig az összes előtte állót es mindenki hallja mindenkinek a hangját.) Mindenki fejére (úgy, hogy nem látja) piros vagy fekete sapkát tesznek. Az embereknek a leghátsótól (N-diktől) kezdve egy színt kell mondani. Ha nem tálalja el a fejen lévő színt, akkor lelövik.
Az N ember, előre milyen stratégiát találjon ki (beszeljen össze), hogy a lehető legtöbb közülük életben maradjon? Mennyi a maximum aki megmenekül és hogyan?
|
|
|
| [591] rizs | 2004-11-20 01:29:21 |
 4 EGYMÁST KÖVETŐ prím kellene :D, hogy számtani sorozatot alkossanak. :D nekem is ez a bajom, hogy ilyet nem találok. elég lenne a legkisebb (akár differencia, akár első tag alapján :))
|
|
| [590] Csimby | 2004-11-20 01:15:18 |
 Most vettem csak észre ezt a hozzászólást. Na mindegy mostmár beírtam feleslegesen a megoldást...
Akkor már mondok egy feladatot is: 116. feladat: Bizonyítsuk be, hogy ha 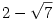 gyöke egy egész együtthatós polinómnak, akkor gyöke egy egész együtthatós polinómnak, akkor 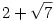 is gyöke. is gyöke.
|
| Előzmény: [582] lorantfy, 2004-11-19 08:15:02 |
|
| [589] Csimby | 2004-11-20 01:05:05 |
 Mivel én adtam fel, én is emlékszem rá : ) A Híres(?)Álbizonyítások témában a [25]-ös.
A villanykapcsolós feladat megoldása: A rabok megszámolják, hogy hányan vannak, aztán kijelölnek egy embert, akinek az lesz a feladata, hogy "számoljonon", legyen ő: A.
Legyen kezdetben a kapcsoló lekapcsolva. Ha valaki felébred, megnézi a kapcsolót, ha le van kapcsolva, akkor felkapcsolja, ha fel van kapcsolva, akkor nem nyúl hozzá. Akkor sem nyúl hozzá, ha már egyszer felkapcsolta. Ez alól csak A kivétel, aki amikor felébred, megnézi a kapcsolót, ha le van kapcsolva, nem nyúl hozzá, ha fel van kapcsolva, akkor lekapcsolja és közben, számolja, hogy hányszor kapcsolta már le a kapcsolót. Amikor ez a szám eléri a (rabok létszáma-1)-et, akkor már biztos, hogy mindenki járt a kapcsolónál. Bővebb indoklást nem írok, szerintem mindenki megérti, hogy ez működik, ha végiggondolja. (Ehhez persze kell az, hogy mindenki "elég" sokszor felébredjen)
|
| Előzmény: [587] rizs, 2004-11-19 15:53:32 |
|
| [588] Hajba Károly | 2004-11-19 23:15:53 |
 Prímek, melyek legalább négytagú számtani sorozatot alkotnak: (részlet :o)
5, 11, 17, 23, 29
131, 191, 251, 311
151, 211, 271, 331
43, 103, 163, 233, 283
47, 107, 167, 227
383, 443, 503, 563
313, 331, 349, 367
47, 89, 131, 173
113, 131, 149, 167
53, 71, 89, 107
227, 269, 311, 353
1087, 1129, 1171, 1213
1373, 1433, 1493, 1553, 1613
1439, 1499, 1559, 1619
Remélem elég lesz?
HK
|
| Előzmény: [583] rizs, 2004-11-19 10:58:15 |
|
| [587] rizs | 2004-11-19 15:53:32 |
 kedves csimbi: nem haragszom meg :) és még egy kérdés: bizonyára emlékezetes mindenki számára az a feladat, hogy elmegy 3 vándor, megszállnak valahol, és akkor 27 vagy 28 aranyat fizetnek... feladat. erről hol találok itt a fórumban valamilyen infót? mintha egyszer láttam volna.
|
|
| [586] Csimby | 2004-11-19 14:26:12 |
 Én ismerek egy megoldást, ott úgyvesszük mintha végtelen hosszú lenne az éjszaka. Úgy tuti nem lehet megcsinálni, ha azt mondjuk, hogy van aki nem ébred fel, vagy kikötjük, hogy valaki max n-szer ébredhet fel (legalábbis amit én ismerek ahhoz az is kell, hogy mindenki akárhányszor felébredhessen és az is kell, hogy ha elég sokáig várunk, akkor egy bizonyos valaki biztosan fel fog ébredni - tekintve, hogy végtelen hosszú az éjszaka, ellentétben az emberek alvásidejével). Lelőjem a megoldást?
|
| Előzmény: [583] rizs, 2004-11-19 10:58:15 |
|
| [585] rizs | 2004-11-19 11:38:47 |
 Legalább hány fős társaságnál lesz 0,5 fölött annak valószínűsége, hogy két embernek ugyanaznap van a születésnapja?
|
|
| [583] rizs | 2004-11-19 10:58:15 |
 Sajnos a feladat kegyetlen módon bánik minden apró részlettel :( "A börtönszokásokhoz tartozik az is, hogy mindenki csak egyedül sétálhat (tehát nem is láthatják a másikat a kapcsolónál) és teljesen véletlenszerű, hogy mikor kit engednek ki sétálni. Semmi garancia nincs arra, hogy mindenki véges időn belül sétálni fog." így esetleg van valami ötletetek? mellé:
114. még egyszer :D: soroljunk négy egymást követő prímet, amelyek számtani sorozatot alkotnak?
illetve egy apró kérdés, amely már itt is biztos elhangzott; ez az oroszlános kérdés, hogy vannak az oroszlánok, ledobnak altatós húst, és akkor jaj mit tegyenek, ezt mondja meg nekem valaki :D
|
|
|
| [581] rizs | 2004-11-19 01:59:16 |
 115. feladat: Van egy börtön, amelynek az udvarán van egy kétállású kapcsoló, véletlenszerű állapotban. A rabok ugyan nem beszélgethetnek, nem adhatnak információt semmilyen módon egymásnak, de bármikor átbillenthetik a kapcsolót a másik állapotába. (A valósággal való egyezés a véletlen műve.) Ebbe a börtönbe visznek N rabot, akik még a rabomobilban összebeszélhetnek. A rabok jól ismerik ennek a börtönnek a szokásait, beeértve a kapcsolót is. Tudják, hogy amikor beviszik őket többet nem beszélhetnek, de "felajánlják" majd nekik, hogy ha mindegyikük már legalább egyszer átállította a kapcsolót és valamelyikük szól, akkor mindegyiküket szabadon engedik. Ha valaki azelőtt szól, hogy valaki még nem nyúlt a kapcsolóhoz, akkor mindenkit kivégeznek. A börtönszokásokhoz tartozik az is, hogy mindenki csak egyedül sétálhat (tehát nem is láthatják a másikat a kapcsolónál) és teljesen véletlenszerű, hogy mikor kit engednek ki sétálni. Semmi garancia nincs arra, hogy mindenki véges időn belül sétálni fog.
Össze tudnak-e beszélni a rabok, hogy szóljon valamelyikük, ha biztosan tudja, hogy mindenki legalább egyszer már hozzányúlt a kapcsolóhoz?
|
|
| [580] rizs | 2004-11-19 01:53:54 |
 még Loríntfy feladta volt annak idején, csak nekem most véletlen kellene a megoldása az 56. feladatnak :) meg lehet tudni? .D:D
illetve még egy remek kis feladat: adjunk meg négy olyan egymást követő prímszámot, amelyek számtani sorozatot alkotnak.
üdv, rizs
|
|
| [579] jenei.attila | 2004-11-18 21:43:23 |
 hasonló módszerrel egyéb érdekes oszthatósági szabályokat lehet találni. Pl. 13|100a+b <=> 13|100a+b-104a-13b 13|-4a-12b <=> 13|a+3b. Itt b már kétjegyű lehet, de b helyett számolhatunk 13-mal való osztási maradékával, vagyis 13|100a+b <=> 13|a+3(b mod 13)
|
| Előzmény: [578] jenei.attila, 2004-11-18 21:17:31 |
|
|
| [577] Hajba Károly | 2004-11-18 19:32:28 |
 A második sor így helyes:
Legyen N=10a+b, akkor minden p-re létezik egy a+j*b kisebb szám, melyik szintén akkor osztható p-vel, mikor N is. Csak a j számot kell ügyesen kitalálni. p=3, j=1; p=13, j=4; p=17, j=5; ...
|
| Előzmény: [576] Hajba Károly, 2004-11-18 19:27:49 |
|
| [576] Hajba Károly | 2004-11-18 19:27:49 |
 Ha valamely p szám 10-zel relatív prím, akkor könnyen készíthető hozzá oszthatósági szabály. Ezek egyikét mutatta be Jenei Attila.
Legyen N=10a+b, akkor minden p-re létezik egy a+j*m kisebb szám, melyik szintén akkor osztható p-vel, mikor N is. Csak a j számot kell ügyesen kitalálni. p=3, j=1; p=13, j=4; p=17, j=5; ...
A p=13-hoz tartozó j=4 a következők szerint adódik, s ez egyben egy kaptafát is ad más oszthatósági szabályok barkácsolásához. Keressük p olyan többszörösét, mely 10 valamely többszörösétől 1 különbséggel adódik. 13, 16, >39<. 4*10 = 3*13 + 1.
N=10a+b
4N-39a=40a-39a+4b
Ha N osztható 13-mal, akkor N=13q
4*13*q-3*13a=a+4b
13(4q-3a)=a+4b
Tehát ekkor a+4b is osztható 13-mal. S ez a első feltételnek megfelelő bármely számra elkészíthető.
HK
|
| Előzmény: [573] zsol, 2004-11-16 17:42:28 |
|
| [575] Csimby | 2004-11-18 17:17:51 |
 Modulo 13, a következő kongruenciák igazak:
100  1, 101 1, 101  10, 102 10, 102  9, 103 9, 103  12, 104 12, 104  3, 105 3, 105  4, 106 4, 106  1, innentől kezdve ismétlődik a kongruencia. Megjegyzed ezt a sorozatot: 1, 10, 9, 12, 3, 4, 1... 1, innentől kezdve ismétlődik a kongruencia. Megjegyzed ezt a sorozatot: 1, 10, 9, 12, 3, 4, 1...
Egy n szám akkor osztható 13-mal, ha a számjegyeiből alkotott kifejezés:
a0+10a1+9a2+12a3+3a4+4a5+a6+10a7+...
osztható 13-mal. Nem mondom, hogy érdemes használni...
|
| Előzmény: [573] zsol, 2004-11-16 17:42:28 |
|
| [574] jenei.attila | 2004-11-18 14:01:47 |
 Szóval: a 13-mal való egyik oszthatósági szabály:
A 10a+b alakú szám pontosan akkor osztható 13-mal, ha a+4b is osztható 13-mal.
A nehezebb rész annak belátása, hogy ha 13|10a+b, akkor 13|a+4. Legyen 10a+b=13n. Ekkor 10|13n-b => 10|39n-3b => (40n-et kivonva)10|n+3b. Legyen ezután k=(n+3b)/10, vagyis n=10k-3b. Ezért 10a+b=13n=130k-39b => 10a+40b=130k => a+4b=13k, vagyis 13|a+4b.
A másik irány bizonyítása könnyebb, az utolsó mondatot kell csak visszafelé értelmezni.
|
| Előzmény: [573] zsol, 2004-11-16 17:42:28 |
|
| [573] zsol | 2004-11-16 17:42:28 |
 Sziasztok , A feladat a következő, mely számok oszthatók 13mal? Mi erre az oszthatósági szabály ?
|
|
| [572] Maga Péter | 2004-11-16 08:49:35 |
 Kedves Attila!
A megoldásod jó. Lényegében én is így csináltam (mármint testbővítéssel).
A megoldásban felhasznált másodfokú testbővítés egyébként is nagyon szép, Surányi László: Algebra-ját ajánlom mindenkinek, akit érdekel a dolog!
|
| Előzmény: [571] jenei.attila, 2004-11-15 23:33:36 |
|
| [571] jenei.attila | 2004-11-15 23:33:36 |
 Válasz Maga Péter feladatára: A nem eleme jelet  helyettesíti, mivel nem találtam megfelelőbbet. helyettesíti, mivel nem találtam megfelelőbbet.
Bizonyítsuk be, hogy minden n 2 természetes számra 2 természetes számra
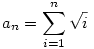
irracionális.
Megoldás:
Tekintsük testek következő, tartalmazásra nézve szigorúan növekvő sorozatát:
Q1 Q2 Q2 Q3 Q3 Q5 Q5 ... ... Qpk Qpk
, ahol Q1 a racionális számok teste, Q2 a Q1  -vel való bővítése, Qpj pedig a Qpj-1 bővítése -vel való bővítése, Qpj pedig a Qpj-1 bővítése 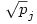 -vel (p1,p2,...,pk az első egymás utáni prímek). Bebizonyítjuk, hogy aj -vel (p1,p2,...,pk az első egymás utáni prímek). Bebizonyítjuk, hogy aj Qpl, de aj Qpl, de aj Qpl-1 valamely l-re (j Qpl-1 valamely l-re (j 1 és l 1 és l 1), amiből következik, hogy an irracionális (n 1), amiből következik, hogy an irracionális (n 2). A sorozat egy testét csak prím négyzetgyökével érdemes bővíteni, mert ha x nem prím, akkor kisebb prímek szorzatára bomlik, amelyek négyzetgyökével már bővítettünk. Prím négyzetgyökével való bővítés pedig valóban bővebb testet eredményez. Ennek bizonyítása teljes indukcióval lehetséges. Mivel 2). A sorozat egy testét csak prím négyzetgyökével érdemes bővíteni, mert ha x nem prím, akkor kisebb prímek szorzatára bomlik, amelyek négyzetgyökével már bővítettünk. Prím négyzetgyökével való bővítés pedig valóban bővebb testet eredményez. Ennek bizonyítása teljes indukcióval lehetséges. Mivel
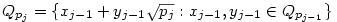
(egyszerű bizonyítani), ezért bármely z racionális szám négyzetgyöke 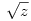 pontosan akkor eleme Qpj-nek de nem eleme Qpj-1-nek (j pontosan akkor eleme Qpj-nek de nem eleme Qpj-1-nek (j 2), ha 2), ha 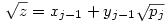 valamely xj-1,yj-1 valamely xj-1,yj-1 Qpj-1. Nyilvánvaló, hogy yj-1 Qpj-1. Nyilvánvaló, hogy yj-1 0, de ha ugyanekkor xj-1 0, de ha ugyanekkor xj-1 0 is teljesülne, akkor négyzetre emelve és átrendezve azt kapnánk, hogy 0 is teljesülne, akkor négyzetre emelve és átrendezve azt kapnánk, hogy 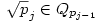 lenne az indukciós feltevéssel ellentétben. Tehát lenne az indukciós feltevéssel ellentétben. Tehát  (z racionális) pontosan akkor eleme Qpj-nek de nem eleme Qpj-1-nek (j (z racionális) pontosan akkor eleme Qpj-nek de nem eleme Qpj-1-nek (j 2), ha létezik yj-1 2), ha létezik yj-1 Qpj-1, amire Qpj-1, amire 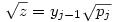 , vagyis , vagyis 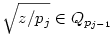 . Másképp fogalmazva: . Másképp fogalmazva: 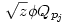 akkor és csak akkor, ha akkor és csak akkor, ha 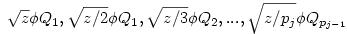 . Ugyanezt a feltételt alkalmazva a feltételben szereplő racionális számok négyzetgyökeire is, azt kapjuk hogy, . Ugyanezt a feltételt alkalmazva a feltételben szereplő racionális számok négyzetgyökeire is, azt kapjuk hogy, 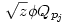 akkor és csak akkor, ha akkor és csak akkor, ha 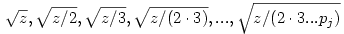 irracionális (ahol a négyzetgyökök nevezőiben a 2-től pj-ig terjedő prímek minden lehetséges szorzata szerepel). Könnyű bebizonyítani, hogy a fenti alakú négyzetgyökök irracionálisak, ha z prím (két négyzetmentes természetes szám hányadosának négyzetgyöke irracionális). Vagyis irracionális (ahol a négyzetgyökök nevezőiben a 2-től pj-ig terjedő prímek minden lehetséges szorzata szerepel). Könnyű bebizonyítani, hogy a fenti alakú négyzetgyökök irracionálisak, ha z prím (két négyzetmentes természetes szám hányadosának négyzetgyöke irracionális). Vagyis 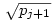 valóban bővíti a Qpj testet. valóban bővíti a Qpj testet.
Vissztérve az eredeti feladatra: azt kell bebizonyítani, hogy ha an Qpj volt (de an Qpj volt (de an Qpj-1), akkor an-hez Qpj-1), akkor an-hez  -et hozzáadva an+1 -et hozzáadva an+1 Qpj vagy an+1 Qpj vagy an+1 Qpj+1 lesz, de nem lehet hogy an+1 Qpj+1 lesz, de nem lehet hogy an+1 Qpj-1 és an+1 Qpj-1 és an+1 Qpjlesz. Vagyis an-hez Qpjlesz. Vagyis an-hez 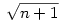 hozzáadásával az adott testben maradunk, vagy eggyel feljebb lépünk, de nem lépünk alacsonyabb indexű testbe. Ha hozzáadásával az adott testben maradunk, vagy eggyel feljebb lépünk, de nem lépünk alacsonyabb indexű testbe. Ha  , vagy , vagy 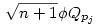 ( ( 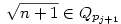 ), akkor nyilván igaz, hogy nem lépünk alacsonyabb indexű testbe. Ha ), akkor nyilván igaz, hogy nem lépünk alacsonyabb indexű testbe. Ha 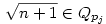 , akkor mint már láttuk, , akkor mint már láttuk, 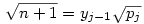 (yj-1 (yj-1 Qpj-1 és yj-1>0) és an hasonló felírásában a Qpj-1 és yj-1>0) és an hasonló felírásában a 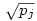 együtthatója szintén pozitív. Ezért ebben az esetben sem lépünk vissza az alacsonyabb indexű testbe. együtthatója szintén pozitív. Ezért ebben az esetben sem lépünk vissza az alacsonyabb indexű testbe.
|
| Előzmény: [523] Maga Péter, 2004-10-09 22:04:22 |
|
|
| [569] matekos04 | 2004-11-09 17:52:26 |
 113 feladat. Udv. mindenkinek!
A feladatom igy szol:
Tegyuk fel hogy van egy digitalis orank. Hany olyan idopont van egy nap alatt (24 h),hogy ha fejtetore allitjuk az orat ugyanazt a szamot kapjuk meg?
|
 |
|
| [568] Maga Péter | 2004-10-28 09:39:55 |
 112. feladat (a 108. feladat folytatása):
Határozzuk meg minden n>1-re azokat az a1,a2,...,an n-eseket, ahol minden ai 0 vagy 1, és
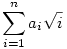 racionális! racionális!
|
|
| [567] Sirpi | 2004-10-22 10:34:40 |
 Megkerestem az ominózus cikket. Úgy tűnik, egyszerűen lemaradt az egyik nyitó zárójel. Az állítás azt mondja ki, hogy minden h>0-hoz van olyan N, hogy minden n>N-re el lehet helyezni legalább 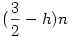 pontot a megadott tulajdonsággal. pontot a megadott tulajdonsággal.
|
| Előzmény: [566] Hajba Károly, 2004-10-22 10:02:38 |
|
| [566] Hajba Károly | 2004-10-22 10:02:38 |
 Megtaláltam a jelzett megoldást a Kömal archivumban 1998/2 66-67. o.
A megj/4. pontban szereplő (3/2)-h)n képlet, mely feltehetőleg nyomdaszedési hiba, értelmezhetetlen. Mi lehet a helyes képlet?
HK
|
| Előzmény: [565] Kemény Legény, 2004-10-21 23:34:45 |
|
|
|
| [563] Hajba Károly | 2004-10-19 15:22:00 |
 Az előző két feladatot egy hálón fellelt gyűjteményből emeltem át. Eredetüket a "közreadója" sem ismeri (Pósa, régi Kömal, ...? :o)
HK
|
|
| [562] Hajba Károly | 2004-10-19 15:19:35 |
 111. feladat:
Tetszőleges n pozitív egészre jelölje f(n) az n szám fordítottját tízes számrendszerben. (Például f(1994)=4991, f(5200)=25.) Keressük meg azokat a pozitív egész k számokat, amelyekre teljesül, hogy tetszőleges n többszörösükre k az f(n)-t is osztja.
HK
|
|
| [561] Hajba Károly | 2004-10-19 15:18:39 |
 110. feladat:
Van egy 101*101-es pontrács. Létezik-e 101 pont úgy, hogy semelyik három nincs egy egyenesen?
HK
|
|
| [560] Suhanc | 2004-10-16 21:07:03 |
 Kedves László!
Köszönöm a segítséget! Elkezdtem megvizsgálni (szigurú értelemben "elkezdtem" , szóval ,mondjuk az első 4 szétbontást;D ), és úgy tűnik, az 1;4 számpár megoldást ad! Eléggé felhősen gondoltam át, szóval könnyen előfordulhat, hogy nem...;D
|
| Előzmény: [559] lorantfy, 2004-10-16 16:35:20 |
|
| [559] lorantfy | 2004-10-16 16:35:20 |
 Kedves Suhanc!
A 102. feladatra gondoltál! Egy kis segítség:
B első megállapításából az derül ki, hogy a szorzat többféleképpen bontható fel két egyjegyű szám szorzatára (továbbiakban szorzatra).
C "Azt én sem" megállapításából pedig az, hogy többféleképpen bontható két egyjegyű szám összegére (továbbiakban összegre).
Abból viszont, hogy mielőtt B nyilatkozott C már tudta, hogy B nem fogja tudni, az derül ki, hogy a C által ismert összeg lehetséges összegre bontásai között nincs olyan amelyik egyféleképpen bontható szorzatra.
Mivel a lehetséges összegek kevesebben vannak (2-20) zárjuk ki először azokat, amelyek összegre bontása egyértelmű.
Majd kizárjuk azokat, melyeknek összegre bontásában van olyan pár, melyek szorzata egyértelműen bontható szorzatra.
Több szám marad, de mivel ezekután B kijelenti: "Akkor már tudom", olyan számot kell keresni a lehetséges szorzatok között, ami csak egy helyen szerepel.
Hát van vele egy kis munka, de ha valaki tud egyszerűbbet, szóljon!
|
| Előzmény: [558] Suhanc, 2004-10-16 14:27:27 |
|
| [558] Suhanc | 2004-10-16 14:27:27 |
 Kedves Mindenki!
Ha valakinek megvan, a 103. feladat megoldása, kérem, írja be, vagy küldje el nekem (suhanc88@freemail.hu)... a számtechtanár napról napra jobban mosolyog... :D
Mivel már elég régóta fenn van, és eddig az édelődés nem volt túl nagy, szerintemolyan is felteheti, aki már ismerte...
|
|
| [557] Hajba Károly | 2004-10-12 22:23:35 |
 Kedves Suhanc!
Sajnos nem jó. Kisértetiesen hasonlít az én első tippemhez, mikor próbáltam megoldani. Én a 11 helyett a 20-at írtam.
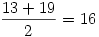 :o( :o(
Egyébként én eddig kétféle megoldását ismerem.
További jó keresgélést minden érdeklődőnek.
HK
|
| Előzmény: [555] Suhanc, 2004-10-12 16:51:08 |
|
| [556] Káli gúla | 2004-10-12 17:07:15 |
 A 104. feladatbeli 2n jegyű számokhoz nem feltétlenül kell programot írni. Egy ilyen, adott hosszú (pl. 100 vagy 2004 jegyű) szám felírása szerintem van olyan érdekes, hogy akár a pontversenyben is ki lehessen tűzni.
|
|
| [555] Suhanc | 2004-10-12 16:51:08 |
 Kedves Onogur!
A szópárbajhoz nem szólnék hozzá (vagytok elegen ;D).
A 109. feladatodra találtam egy lehetséges megoldást!
Az életkorok: 1;2;4;8;11;13;16;17;19. Nyilván csak akkor lesz az átlag egész, ha a kiválsztott két szám paritása megegyezik. Végignézve az eseteket, látható, hogy a feladat feltételeinek megfelelnek.
De vajon van-e másik?:D
|
| Előzmény: [543] Hajba Károly, 2004-10-11 12:00:20 |
|
| [554] Hajba Károly | 2004-10-12 14:34:04 |
 Kedves Edgar!
Csak a vicc kedvéért tippeld meg, de akár bárki más is, hogy javíthatók-e Erich Friedmann feladatai a nem széteső azonos idomok körében itt n= 7, 10, 13 esetében, s ha igen, milyen mértékben? Ezen feladathoz nem kell kemény tárgyi tudás, tudni, hogy mi hol van, csak egy kis kreatív fantázia. Remélem Ti azzal is rendelkeztek. Vagy nem? :o)
Üdv: HK
|
| Előzmény: [552] Edgar, 2004-10-11 21:48:37 |
|
| [553] Hajba Károly | 2004-10-11 22:17:27 |
 Kedves Edgar!
Eredetileg én az n=5-ről nem állítottam, hogy meg lehet oldani. Én azt mondtam, hogy szerintem az n=7 és 13-on lehet javítani. Ezt KL dobta fel, tudjuk viccesen, s ezen már túl is léptünk.
Egyébként, ha megfigyeled, rendszeresen használom a smile-t. S a minap jól jöttél volna a svédek ellen. :o)
Üdv: HK
|
| Előzmény: [552] Edgar, 2004-10-11 21:48:37 |
|
| [552] Edgar | 2004-10-11 21:48:37 |
 Kedves Károly! (...) Ne vedd a szívedre nagyon, egy kis humorérzék talán jobban kezeli a konfliktusokat, mint az, ha megoldatlan problémára invitálod a vitapartert... :) én is tudok 10-20 megoldatlan feladatot, ha szükség lenne rájuk :))
Kedves Dávid! Sajnos nem értek a numerológiához, és szívesen fejleszteném a lényeglátásomat, ezért hadd kérdezzem meg: miben különleges a 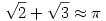 közelítés? közelítés?
Tisztelettel:
Edgar Davids
|
| Előzmény: [551] Hajba Károly, 2004-10-11 20:44:27 |
|
|
|
|
| [548] Csimby | 2004-10-11 19:40:21 |
 Miért? Szerintem ez tök poén! Mindenki keresi az összefüggőt ami valószínű nincs is és akkor itt van a triviális megoldás nem összefüggőre. (nem volt kikötve, hogy legyen összefüggő :-)
|
|
| [547] Hajba Károly | 2004-10-11 19:33:22 |
 Kedves Sambuca!
Hát mit modjak? Anno az én időmben erre azt mondták: Ha nem mondod, hülyén halok meg. :o)
Tudom, hogy tudod, hogy...
Tehát nem ez a feladat. Netalántán az igazi feladatba beletörött a bicskátok? :o)
HK
|
| Előzmény: [544] SAMBUCA, 2004-10-11 17:38:05 |
|
|
| [545] Csimby | 2004-10-11 18:22:32 |
 Nem összefüggőre elég könnyű, itt van 5-re, ez n-re is működik...
|
 |
|
| [544] SAMBUCA | 2004-10-11 17:38:05 |
 Kedves Onogur!
Kemeny Legenyhez hasonloan En is fel tudom osztani az L alakot 5 (n) egybevago reszre.
//Persze az egyes reszek nem osszefuggoek, de ettol meg egybevagoak//
Ez lehet akar a 110. feladat is.
SAMBUCA ( HOMI) HOMI)
|
|
| [543] Hajba Károly | 2004-10-11 12:00:20 |
 109. feladat:
Egy embernek 9 gyereke van, mind 1 és 20 éves között (ikrek nincsenek). A gyerekek között nincs három olyan, hogy közülük a fiatalabb és az idősebbik életkorának átlaga pont a középső életkorát adja. Hány évesek a gyerekek?
HK
|
|
| [542] Hajba Károly | 2004-10-11 11:57:59 |
 Az indulatok hevében és figyelmetlenségek miatt felborult a feladatszámozások rendje, melyet most megpróbálok rendezni:
[502] Homi(Sambucs?) mágikus számozású feladat sorszáma: 106.
[508] Sambuca 'just for fun' feladata: 107.
[524] Maga Péter feladata: 108.
Üdv: HK
|
|
|
| [540] Hajba Károly | 2004-10-11 07:41:21 |
 Kedves Sambuca!
Köszi! Ennyi elég a tisztességnek, hogy közlöd, egy saját rutinnal állítottad elő. Egyébként kiváncsi vagyok, hogy milyen - egyébként bizton állíthatom, hogy nemlétező - titkolt szándékot vélsz felfedezni a feladat kiírásában. Ezt egy másik fórumban láttam és megtetszett, érdekesnek tűnt számomra. De látom, neked is tetszik, s ennek nagyon örülök.
Üdv: HK
|
| Előzmény: [528] SAMBUCA, 2004-10-10 19:36:26 |
|
|
|
|
|
| [535] V. Dávid | 2004-10-10 21:07:22 |
 Semmire. Ami ott szerepel, az egy teljesen használhatatlan állítás. Kizálólag érdekességnek jó. Ezért csodálkoztam, hogy hogy jön ide, hogy ennél már a kínaiak is jobban megközelítették a  -t. -t.
|
| Előzmény: [534] Kemény Legény, 2004-10-10 20:57:23 |
|
|
| [533] V. Dávid | 2004-10-10 20:52:31 |
 Neked meg a diákolimpiás topikban lévő 15-ös hozzászólásod volt rendkívül építő jellegű. Nézd meg még egyszer, amit írtam, és gondolkozz el azon, mit a lényege. Nem az, hogy minnél jobban megközelítse a  -t. -t.
|
| Előzmény: [532] Kemény Legény, 2004-10-10 20:29:50 |
|
|
|
|
| [529] V. Dávid | 2004-10-10 20:11:24 |
 Fantasztikus numerológiai felfedezés:
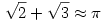
|
|
| [528] SAMBUCA | 2004-10-10 19:36:26 |
 Kedves Onogur!
A megoldasok 50-50%-ban az agyam illetve egy szamologepes program termeke. (A program forraskodjat is en irtam :) )
Mar latom, hogy mire megy ki a feladat, de ezt meg nem arulnam el, csak majd ha meglesz az altalanos megoldas.
|
| Előzmény: [525] Hajba Károly, 2004-10-09 23:18:25 |
|
| [527] Gubbubu | 2004-10-10 14:16:44 |
 Úgy látom, ez nehéz feladatnak bizonyult. Segítek a többieknek: a Google-ban nem árt rákeresni az Erdős, a Ginzburg és a Ziv keresőszavakra. Akár így együtt. Üdv:G.
|
| Előzmény: [501] HOMI, 2004-10-08 12:13:20 |
|
| [526] Csimby | 2004-10-10 01:06:52 |
 Sziasztok!
Jó régen nem írtam ide (winchester tönkrement, táborok, tanulás stb.). És most is egy saját hozzászólásomra reagálok :-) A SET nevű játékról van szó és arról, hogy hány kártyát kell kirakni ahhoz, hogy biztosan legyen benne set. Itt van egy link ahol 20 kártyát raknak ki úgy, hogy nincsen benne set. Látom megint téma volt a Stetson-on található Packing problámák egyike, Muy Bien. Na jó szórakozást...
|
| Előzmény: [436] Csimby, 2004-07-23 18:36:33 |
|
| [525] Hajba Károly | 2004-10-09 23:18:25 |
 Kedves Sambuca!
Kapom, kapkodok a levegő után csodálkozásomban. Csodálom kitartásodat, hogy mind a 108 lehetőséget végigszámoltad. De ha másodpercenként egyet át is vizsgálsz, az évek sora?! Azaz nyílvánvaló, hogy valahogy másképp csináltad. Progival vagy levezetted? Illő lenne titkodat elárulni. Látod Suhanc szépen levezette a feltehetőleg számodra érdektelen feladat megoldását.
Mindentől függetlenül - bárhogyan is leltél a megoldásra - gratulálok Neked. De miről is akarsz meggyőzni? :o)
Üdv: HK
|
| Előzmény: [521] SAMBUCA, 2004-10-09 03:20:17 |
|
| [524] Hajba Károly | 2004-10-09 23:05:24 |
 Kedves Suhanc!
Szép megoldásodhoz gratulálok.
Bevallom őszintén, az utóbbi feladatok hozottak, sőt erős gyanúm szerint mind keményen madárlátta. Ti. ahonnan hoztam oda is hozták valahonnan egy általam ismeretlen helyről. Létezik egy feladatfeladós hely, egyszer rá is találtam úgy másfél hónapja, de sajnos a NAV hathatós segítsége mellett begyűjtöttem egy kiírhatatlan kémvírust, mely miatt alaklmazni kellett a cformat-ot. Így egy csomó linkemtől megszabadultam.
Általában mondom, hogy a háló teljes mértékben nyílvános és szabad hely. Ha valamit fellelsz rajta, általában szabadon használhatod nem üzleti célra ill. ha nem követsz el vele etikai vétséget. Így az itt feltett feladatokat is minden engedély nélkül feladhatod a sulidban, csak jelezd, hogy a hálón találtad és kész. Etikátlan a pontversenyen kitűzött feladazokat más fórumon feladni és ilyen módon begyűjteni a megoldást.
HK
|
| Előzmény: [522] Suhanc, 2004-10-09 13:34:46 |
|
| [523] Maga Péter | 2004-10-09 22:04:22 |
 Üdv mindenkinek!
Egy szép feladat (sajnos nem saját):
Bizonyitsuk be, hogy minden n>1 egészre
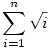 irracionális! irracionális!
|
|
| [522] Suhanc | 2004-10-09 13:34:46 |
 Kedves Onogur!
Hát itt eléggé begyorsultak a hozzászólások,és már nem nagyon követtem... a 103. feladatodra viszont, ha jól láttam, még nem válaszolt senki! Először is: Nagyon ötletes!!!:) Ha saját, akkor őszintén gratula! Ha láttad valahol, leírnád, hol találok még ilyeneket? /ja, és ha nem probléma, ezt is "elkérném" matekórára ;D/
A megoldásom:
A 6. állítás nyilvánvalóan hamis! Tehát 6-os nincs a számban, az azonban osztható hattal! Ebből az is következik, hogyaz első állítás is hamis, tehát egyes sincs benne!
Innen esetszétválasztással oldjuk meg!
Tfh: a 2. állítás igaz!Ekkor 0 nem lehet benne, mert az csak a legelső helyre kerülhetne! Tehát a 0. álllítás is hamis!
Ha minden számjegy kisebb, mint a következő, akkor nincs két egyforma, tehá a hármas állítás is igaz, így a számban 3-as is van! Ezzel megcáfoltuk a nyolcas állítást, mert 3-2=1! Tehát nyolcas nincs benne!
A negyedik állításnak hamisnak kell lennie,különben az ötös állítás hamis, tehát a szám legalább 6 jegyű, de csak a 2;3;4 számjegyek építik fel, és nincs ismétlődés! Ez nyilvánvalóan lehetetlen. Az ötös állítás viszont igaz, mert 5 féle számjegyet (0; 1;4;6;8) már kizátunk, és nem lehet ismétlődés!!! Ekkor a 9. állítás is igaz, mert 2+3=5! Mivel az eddig kiválasztott számok (2;3;5;9), és a még nem vizsgált számok (7) között csak a 2 a páros, és az sem állhat a végén( a második állítás miatt), ezért a 7. állítás nem igaz! Ekkor a 2;3;5;9 számokból felépülő egyetlen lehetsége megoldás a 2359! Ez azonban tesz eleget a 0., hamis állításnak, tehát ez sem jó megoldás!!!
Ha a 2. állítás hamis:
Ha a 8. állítás hamis lenne, akkor a 4. állítás biztosan igaz lenne, mert csak a 3 4;5 számok vannak egymás mellett azok közül, amelyeket még nem lőttünk ki! Ha 4 igaz, akkor 5;7,9 hamisak,ezért a 3. igaz, ekkor azonban az 5. állítás hamissága miatt ellentmondásra vezet!()hasonlóan az előző esethez!)
Tehát a 8.állítás igaz! Emiatt a 7. és a 9.állítás hamis, valamint a 8. állítás igaza megcáfolja a 4. állítást, ezért a is hamis!
Összesítve: ez esetben ídáig 1;2;4;6;7;9 hamisak, és 8 igaz! Ekkor nem lehet 3 és 5 is igaz, mert akkor 3+5=8, és ekkor 9 igaz lenne! De mindkettő hamis sem lehet, mert akkor nem lesz PN számjegy a számban, és akkor 7. igaz lenne!
Ha 5. hamis, és 3. igaz, akkor legfeljebb 3 számjegyből áll a szám(0;3;8), és 5. hamissága miatt leglább hatjegyű, persze, ismétlés nélkül!:D Tehát ez megint ellentmondás!
Tehát 5.igaz, és 3. hamis!
Mivel a szám 6-tal osztható, ezért kell lennie 0-s számjegynek is! Mievl 3. hamis, ezért van ismétlődő számjegy! Azonban 5 vagy 8 nem ismétlődhet, mert akkor 5+0=5 és 9. igaz lenne! Ugyanezen okokmiatt nem leht a számban 3db 0! Ezen okok miatt az egyetlen lehetséges megoldás 8005!!!
|
| Előzmény: [497] Hajba Károly, 2004-10-06 09:07:13 |
|
|
|
|
|
| [517] Lóczi Lajos | 2004-10-09 00:16:21 |
 Olyan is van sok. Az 19860311 után következő legközelebbi ilyen prímek, amelyek tehát születési dátumként is értelmezhetők, és megfelelnek a feladat kritériumának: 19860727, 19870831, 19900403, 19910809, 19920713, stb...
Persze hogy nem fejben számoltam:) A következő egyszerű Mathematica-utasítás kész formában adja az eredményt (az eredeti feladatét, nem a "dátumosét"; az utasítás vége felé lehet beállítani, hogy hányadik prímtől hányadikig vizsgálja át a prímeket - itt olyan határokat adunk meg, hogy a 8-jegyű prímek között maradjunk...)
Prime[Drop[ Union[Table[ If[{a, b, c, d, e, f, g, h} = IntegerDigits[Prime[n]]; PrimeQ[FromDigits[{a, b, c, d, e, f, g, h, a, b, c, d, e, f, g, a, b, c, d, e, f, a, b, c, d, e, a, b, c, d, a, b, c, a, b, a}]], n], {n, 1265000, 1266000}]], -1]]
|
| Előzmény: [515] SAMBUCA, 2004-10-08 23:36:51 |
|
| [516] Hajba Károly | 2004-10-09 00:08:04 |
 Kedves Sambuca!
Te keresésben jó vagy, de gondolom az agyad is élesre van köszörülve, így remélhetőleg tudsz segíteni a következő probléma megoldásában is, melyet előre is megköszönök Neked.
Nos Vízi Dávid hozott a 98. feladatban [472] egy - számomra mindenképpen - érdekes problémát, melyet innen merített. N=5-re feltehetően nincs már jobb megoldás, de szerintem n=7-re vagy n=13-ra létezik jobb megoldás is. Olyan snassz, hogy csak téglatestek vannak lepakolva. Titkolják vagy még nem találták meg? Nem jobban néznének ki az ábrák, ha ez lenne aláírva:
Found by SAMBUCA in 2004 vagy esetleg Found by Onogur in 2004. :o)
Mit gondolsz, s(7) és s(13) meddig csökkenthető?
Üdv: HK
|
|
|
| [514] Lóczi Lajos | 2004-10-08 23:29:47 |
 Úgy tűnik, rengeteg ilyen prím van. Például az első száz ilyen tulajdonságú prím az alábbi: 10000079, 10000721, 10001213, 10001461, 10001707, 10002067, 10002203, 10002589, 10003247, 10003879, 10004207, 10005431, 10005833, 10005953, 10007359, 10007537, 10007707, 10008371, 10009381, 10009871, 10010141, 10011247, 10012213, 10012351, 10012757, 10013147, 10013747, 10014341, 10014379, 10014941, 10015487, 10016693, 10016911, 10016917, 10017613, 10017809, 10020853, 10021129, 10021147, 10021723, 10022251, 10022543, 10023691, 10023901, 10024193, 10024499, 10024507, 10024909, 10025879, 10025933, 10026287, 10026901, 10027159, 10028581, 10028587, 10029049, 10029931, 10030103, 10031929, 10032053, 10032989, 10033169, 10033409, 10033571, 10033763, 10033981, 10034537, 10035169, 10035833, 10036127, 10036357, 10037207, 10037389, 10038659, 10039093, 10039273, 10039577, 10040117, 10040269, 10041749, 10042289, 10042757, 10042759, 10042883, 10043699, 10043911, 10044113, 10044313, 10045379, 10045627, 10045949, 10046807, 10047319, 10048331, 10048789, 10051367, 10052377, 10052663, 10053157, 10053301.
|
| Előzmény: [507] SAMBUCA, 2004-10-08 21:44:15 |
|
|
|
| [511] SAMBUCA | 2004-10-08 22:39:45 |
 hat igen: a,s,d,f,g,h,j,k = a,b,c,d,e,f,g,h
|
|
|
|
|
| [507] SAMBUCA | 2004-10-08 21:44:15 |
 Itt egy erdekes feladat: /just for fun/
Keressunk olyan 8jegyu abcdefgh alaku primszamot (a,s,d,f,g,h,j,k nem feltetlenul kulonbozo nemnegativ egeszek, a 0 ), hogy abcdefghabcdefgabcdefabcdeabcdabcaba 0 ), hogy abcdefghabcdefgabcdefabcdeabcdabcaba
is prim legyen!
|
|
| [506] SAMBUCA | 2004-10-08 20:58:51 |
 Bocsanat. Majd elfelejtettem a legkevesebb oldallal rendelkezo szabalyos testet a tetraedert.
|
|
|
|
| [503] Hajba Károly | 2004-10-08 13:57:02 |
 Kedves Sambuca!
-Ki állította, hogy lehet?
-Ki mondta, hogy ide csak matekolimpián szerepeltek?, kiemelt matektagozatosok, szuperzsenik (mint pl. Te) írhatnak?
-Kinek van meg a Rieman?
De ha Te ennyire okos vagy, kérlek segíts! Nem kaptam még választ egy számomra megoldhatatlannak tűnő kérdésre, melyet a Geometria 27. feladatában adtam fel. Gondolom Te tudod, hol található rá válasz?
Üdv: HK
|
| Előzmény: [500] SAMBUCA, 2004-10-08 12:03:33 |
|
| [502] Moderátor | 2004-10-08 12:58:20 |
 Kedves SAMBUCA/HOMI,
Ha lehet, kicsit fogd vissza magad. Megmondhatod, hogy ez vagy az a tétel ismert, vagy neked melyik feladat (nem) érdekes és miért, de lehetőleg olyan modorban, hogy ez senkit se sértsen.
M.
|
| Előzmény: [500] SAMBUCA, 2004-10-08 12:03:33 |
|
| [501] HOMI | 2004-10-08 12:13:20 |
 Bocsi hogy csak így. De most ezek télleg érdekes feladatok? Mondok egy érdekes feladatot: 666. feladat: Adott 2n-1 egész szám. Biz. be, hogy kiválasztható közülük pontosan n úgy, hogy összegük n-nel osztható. Kellemes gondolkozást!!!!! Üdv. HOMI
|
|
|
| [499] Hajba Károly | 2004-10-08 01:05:14 |
 105. feladat:
Fel lehet-e osztani egy 60 egységnyi oldalú kockát kisebb kockákra úgy, hogy minden kisebb kocka élei különböző egész számú egységnyi hosszú legyen?
HK
|
|
| [498] Hajba Károly | 2004-10-08 01:00:59 |
 104. feladat:
1233=122+332
990100=9902+1002
Az ennél többjegyűbb számok között van-e olyan, amire ez teljesül, tehát felbonható 2*n jegyű szám 2 db n-jegyű szám négyzetösszegére a fenti szinsztéma alapján?
HK
|
|
| [497] Hajba Károly | 2004-10-06 09:07:13 |
 103. feladat:
Az alábbi listában igaz és hamis állítások vannak, melyek egy tizes számrendszerbeli pozitív egész számra vonatkoznak. Ha az állítás igaz, a sorszáma számjegye szerepel a szám számjegyei között, ha hamis, akkor nem szerepel:
0. A számjegyek összege prímszám.
1. A számjegyek szorzata páratlan.
2. Minden egyes számjegy kisebb, mint a következő.
3. Nincs két egyenlő számjegy.
4. Egyik számjegy sem nagyobb, mint 4.
5. A számnak kevesebb, mint 6 számjegye van.
6. A számok szorzata nem osztható 6-tal.
7. Páros számról van szó.
8. Nincs két olyan számjegy, amelynek a különbsége 1.
9. Létezik legalább egy olyan számjegy a számban, amely két másik benne lévő számjegynek az összege.
Melyik számról van szó?
HK
|
|
| [496] Hajba Károly | 2004-10-04 22:02:24 |
 Kedves László!
Köszi az alapos és kidolgozásához feltehetően sok türelmet igénylő megoldásvázlatodat. A feltehetően többtízezres számoságú megoldás miatt nem véletlen, hogy könnyen talál az ember egy-egy példát rá.
HK
|
| Előzmény: [495] lorantfy, 2004-09-25 14:01:51 |
|
| [495] lorantfy | 2004-09-25 14:01:51 |
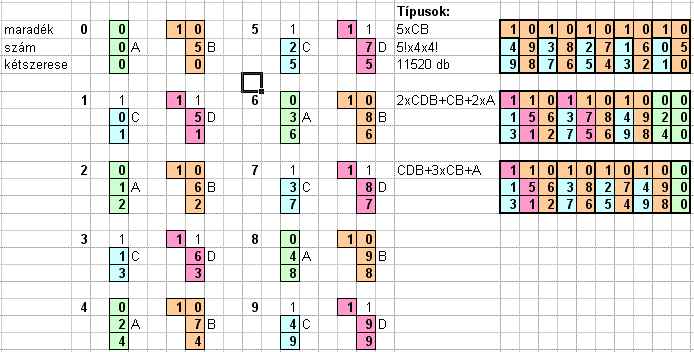
 101/b feladat megoldása: Valahogyan rendszereznünk kell a megfelelő 10 jegyű számokat. Először is nézzük meg melyik számjegy hogyan állítható elő egy másik számjegy kétszereseként. Páros szájegyeknél A és B, páratlanoknál C és D előállítás lehet. Írjuk fel a számot és kétszeresét egymás alá és föléjük pedig a maradékokat. Egy 10x3-as táblát kapunk, melyet az előbbi A,B,C,D mintákból kell kiraknunk.
A legegyszerűbb kirakás, hogy a páros számjegyeket B, a páratlanokat C formában állítjuk elő. Ezek szépen összeillenek és kitöltik a táblát. A B-ket bármilyen sorrenben rakhatjuk: 5!. A C-k közül az 1C-t nem rakhatjuk előre a 0 miatt: 4x4!. Így ebből a típusból: 5!x4x4!=11520 van.
Második lehetőség: a C,D és B mintákból 3x3-as egységeket képezhetünk. A D-khez csak C minták párosíthatók, viszont mindketten páratlan számjegyeknél vannak, így az 5 féléből legfeljebb 2 CD párt rakhatunk össze. A maradó egy páratlan számnál a C mintát B-vel párosítjuk. Így 3 B-t használtunk a páros számok közül. A megmaradó 2 páros számnál csak az A mintát választhatjuk.
Harmadik lehetőség: egy CDB hármashoz 3 CB pár és egy A minta, ami nem lehet más mint a felhasznált D minta előtt álló páros szám A mintája.
A második és harmadik lehetőség elemszámának meghatározása legyen a 101/c feladat!
|
 |
| Előzmény: [491] Hajba Károly, 2004-09-18 12:47:00 |
|
| [494] Suhanc | 2004-09-19 09:05:31 |
 Ezt a feladatot egy számtechtanár mesélte a sulinkban. Aki ismeri, ne lője le!
102.Feladat
A történet három emberről, A-ról, B-ről és C-ről szól. "A" gondolt két, nem feltétlen különböző, 1-és 10 közé eső pozitív egész számra!(zárt intervallum) B-nek megmondta a szorzatukat, C-nek az öszegüket. Az alábbi párbeszéd zajlott le:
B: Nem tudom, melyik két számra gondolt A!
C: Azt én sem, de azt tudtam,hogy Te sem tudod!
B:Akkor tudom, melyik két számra gondolt!
C: Akkor én is!
|
|
| [493] Hajba Károly | 2004-09-18 15:20:41 |
 Valóban csak 3 felel meg a feladat kiírásának, de a másik kettő is érdekes eredményt adott. :o)
Ezen túlmenően találtam még több megoldást is, de rendszert még nem sikerült rá felfedeznem.
HK
|
| Előzmény: [492] lorantfy, 2004-09-18 13:56:34 |
|
| [492] lorantfy | 2004-09-18 13:56:34 |
 Kedves Károly!
Szépek a számok! (De csak 3 db jó!) Kösz a megoldást! Én a 9876543210 számot osztottam 2-vel és 4938271605 jött ki. Így keletkezett a feladat, de érdemes továbbfejleszteni.
|
| Előzmény: [490] Hajba Károly, 2004-09-18 11:54:50 |
|
|
| [490] Hajba Károly | 2004-09-18 11:54:50 |
 Kedves László!
A 101. feladat megoldása:
Legyen A=1.234.567.890, ekkor 2*A=2.469.135.780; 4*A=4.938.271.560; 5*A=6.172.839.450; 7*A=8.641.975.230 és 8*A=9.876.543.120. Így legalább 5 ilyen szám létezik, de nincs kizárva, hogy több is lehetséges. (Az a fránya 3-as nem szereti a rendet :o)
HK
|
| Előzmény: [489] lorantfy, 2004-09-18 09:56:01 |
|
| [489] lorantfy | 2004-09-18 09:56:01 |
 Kedves Fórumosok!
Szép volt a 100. feladat, gratula Sirpinek és a megoldóknak!
101. feladat: Van-e olyan tizes számrendszerbeli szám, amely 10 különböző számjegyből áll és kétszerese is 10 különböző számjegyből áll?
|
|
| [488] Sirpi | 2004-09-16 09:38:04 |
 Pontosan, valóban ez a megoldás.
Vagyis úgy is fogalmazhatunk, hogy az ak-1 alakú számok közül a legnagyobb közös osztó művelete nem vezet ki, azaz az eredmény is épp ilyen alakú, és a kitevő a két szám kitevőjének lnko-ja.
|
| Előzmény: [487] nadorp, 2004-09-16 08:09:37 |
|
|
| [486] Hajba Károly | 2004-09-15 23:34:26 |
 Kedves Sirpi!
Tipp a 100. feladathoz:
Erős gyanúm, hogy általában LNKO=a-1. Legyen m>n. N=an-1+an-2+...+1 és M=am-1+am-2+...+an. Így
an-1=(a-1)N és am-1=(a-1)(M+N).
Az 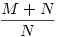 törtnek akkor van egész értéke, ha m n-nek egész számú többszöröse. Ekkor LNKO=an-1, hiszen: törtnek akkor van egész értéke, ha m n-nek egész számú többszöröse. Ekkor LNKO=an-1, hiszen:
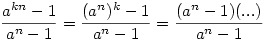
HK
|
| Előzmény: [485] Sirpi, 2004-09-15 13:23:37 |
|
| [485] Sirpi | 2004-09-15 13:23:37 |
 100. feladat: Mennyi a legnagyobb közös osztója az an-1 és az am-1 számoknak, ha n és m természetes számok, a pedig pozitív egész? (A feladat saját ötlet, nem nehéz, de bevallom, először meglepődtem a végeredményen.)
|
|
| [484] V. Dávid | 2004-09-14 22:54:04 |
 http://www.infinity.tag.hu/ :-))))))))))))))))))))))))))))))))))))))))
|
|
| [483] Hajba Károly | 2004-09-14 15:25:15 |
 Kedves Dávid és Topik!
Kicsit visszatérnék a 98. feladat témájához. Erich Friedman a honlapján bemutatja, hogyan lehet az L-idomba n db egybevágó idomot beilleszteni úgy, hogy az a lehető legjobban kitöltse az L-idomot. Ezek az ezidáig talált legjobb megoldások?
HK
|
| Előzmény: [474] V. Dávid, 2004-09-04 13:06:15 |
|
| [482] jenei.attila | 2004-09-14 13:21:11 |
 Közben megtaláltam a feladatot, és pontosan erről van szó. Kezdetben valóban páratlan sok kavicsot tartalmaz a kupac. Továbbra is érdekelne, hogy honnan származik ez a feladat, és aki nem ismerte, annak sok sikert a megoldáshoz (bár egy kicsit segítettem azzal, hogy elárultam kinek mikor van nyerő stratégiája).
|
| Előzmény: [481] jenei.attila, 2004-09-14 12:41:21 |
|
| [481] jenei.attila | 2004-09-14 12:41:21 |
 Sziasztok!
Egy kis segítségre lenne szükségem. Úgy két két és fél éve megoldottam egy feladatot, amelyből csak egy kis darab papírt találtam meg. Sajnos ennyiből nem jöttem rá mi is volt a feladat, de valami olyasmi hogy egy kupac kavicsból két játékos felváltva vesz el 1 2 vagy 3 kavicsot, és végén az nyer, akinél páros sok kavics lesz. Lehet hogy kiindulásnál páratlan sok kavics volt, erre már nem emlékszek. Sajnos a feladatot sehol nem találom, de a megoldás talán az volt, hogy a kezdőnek van nyerő stratégiája, ha kezdetben nem 8k+1 számú kavics volt a kupacban. Ellenkező esetben a második játékos tud nyerni. Szóval a feladat kellene pontosan.
|
|
|
|
|
|
|
|
|
| [472] Hajba Károly | 2004-09-04 10:25:06 |
 Kedves Dávid!
Még nem volt ilyen példa. S mivel a diszkrét matematika "csempézős" (alias pakománia) feladatkörében igen nehéz a bizonyítás vagy cáfolat, így feltehetően létezik megoldás. (Agyam felizzott :o)
HK
|
| Előzmény: [471] V. Dávid, 2004-09-04 09:40:11 |
|
| [471] V. Dávid | 2004-09-04 09:40:11 |
 98. Feladat (Remélem, ez még nem volt) Három, egységnyi oldalú négyzetet L-alakban egymáshoz illesztünk (vagy egy 2 oldalú négyzetből levágunk egy 1 oldalút) Fel lehet-e darabolni ezt öt egybevágó részre?
|
|
|
| [469] Lóczi Lajos | 2004-09-03 22:00:11 |
 Kedves Dávid,
a "selytésed" :) helyes. Páratlan n-re a sokdimenziós gömbök térfogatának és felszínének elemzése megtalálható a http://mathworld.wolfram.com/Hypersphere.html címen.
|
| Előzmény: [468] V. Dávid, 2004-09-03 21:34:13 |
|
| [468] V. Dávid | 2004-09-03 21:34:13 |
 A 95. általánosítása: Vegyünk három helyett n darab számot. A keresett P(n) valószínűség az egységsugarú n-dimenziós gömb G(n) és a két egység oldalú n-dimenziós kocka K(n) térfogatának aránya. Nyilván K(n)=2n, de mi a helyzet G(n)-nel?
Nézzük meg, hogyan is számoltuk ki a gömb térfogatát. Adott az origó középpontú, r sugarú k kör. Most x szerint integráljuk azoknak a köröknek a területét, amelyek sugara egyenlő k x-hez tartozó y koordinátájával. 4 dimenzióra analogikusan gondolkodunk: Adott az előző k kör. Most x szerint integráljuk azoknak a gömböknek a térfogatát, amelyek sugara k x-hez tartozó y koordinátája, azaz
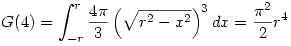
Hasonlóan 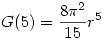 . Kipróbáltam az első néhány n-re, és az a sejtésem alakult ki, hogy . Kipróbáltam az első néhány n-re, és az a sejtésem alakult ki, hogy
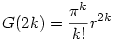
De semmilyen selytésem nem alakult ki páratlan n-re.
|
| Előzmény: [466] lorantfy, 2004-09-03 12:05:45 |
|
| [467] Káli gúla | 2004-09-03 12:33:30 |
 Kedves Károly!
A kettes találathoz nem kell minden párt eltalálni. Például, minden nyerő ötösben van két szám, ami néggyel osztva azonos maradékot ad, így elég az ilyen párokat eltalálni. Leírok egy rendszert, amivel 30 szelvényen mindig lesz 2 találatunk, feltéve, hogy a nyerő ötösben van két 4-gyel osztható szám. Ezt a 30 szelvényt 0-val, 1-gyel, 2-vel és 3-mal eltolva kaphatunk 120 szelvényt, ami garantál 2 találatot. Ez nem optimális, de nincs nagyon messze attól. A pontos szám 100 körül lehet, ahogy írtad.
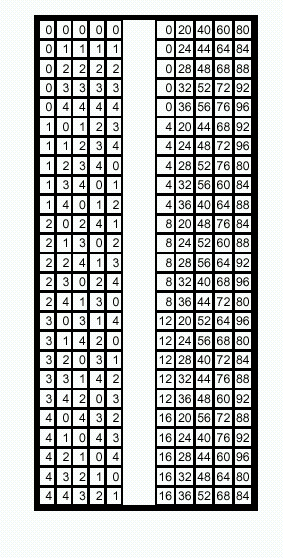
Az egyszerűség kedvéért 100-ig nézzük a számokat, a 25 néggyel osztható számból alkotható összes párt, másképp mondva a 25 csúcsú teljes gráf éleit akarjuk 30 ötössel lefedni. A 25 számot 5 ötös csoportba osztjuk: (0,4,8,12,16), (20,24,28,32,36), ..., (80,84,88,92,96). Először is a "belső élekhez" ezt az 5 ötöst megjátszuk 1-1 szelvényen.
Ezután, mivel két ötös csoport "között" 25 él lehetséges, a "köztes" élek lefedéséhez azt kell csak megoldani, hogy azok mind előforduljanak valamelyik szelvényünkön. Indexeljünk egy-egy ötös csoporton belül 0, 1, ..., 4 - gyel, és készítsünk egy olyan táblázatot, ahol bármely két oszlopot végignézve (az oszlopok az ötös csoportoknak felelnek meg), minden lehetséges párt megtalálhatunk. Ilyen táblázat 25 sorát az
(i,j,i+j,2i+j,3i+j), (i,j=0,..,4)
ötösökkel lehet elkészíteni, ezt mutatja az ábra bal oldali része, a jobb oldali részen pedig a nekik megfelelő 25 lottószelvény található (a nem létező lottószámokat tetszőleges másik számmal kell helyettesíteni).
|
 |
| Előzmény: [455] Hajba Károly, 2004-09-01 15:46:40 |
|
| [466] lorantfy | 2004-09-03 12:05:45 |
 Hello Fiúk!
Ez tényleg sokat segít. Ha a kiválasztott három számot térbeli koordinátákként fogjuk fel, akkor az összes lehetséges pont egy 2 egység oldalú kockát ad. A négyzetösszegük a pont origótól vett távolságának négyzete. Így a jó pontok egy egység sogarú körben vannak. A térfogatok aránya adja a keresett valószínüséget. Majd otthonról felteszek egy 3D-s ábrát hozzá.
|
| Előzmény: [463] Sirpi, 2004-09-02 22:48:28 |
|
| [465] V. Dávid | 2004-09-03 10:13:45 |
 97. Feladat: Hozzunk létre olyan sík-koordináta-rendszert, amelyben a sík minden pontjának egyetlen koordinátája van.
|
|
| [464] V. Dávid | 2004-09-03 10:07:10 |
 Aki nem jön rá a trükkjére, és algebrai módszerekkel akarja megoldani, az reménytelennek találja a feladatot. Egyszer fealdtam egy nagyon jó matekos srácnak, aki emiatt nem tudta megoldani.
|
| Előzmény: [463] Sirpi, 2004-09-02 22:48:28 |
|
|
| [462] V. Dávid | 2004-09-02 20:47:19 |
 96. Feladat: a [-1;1] intervallumból véletlenszerűen kiválasztunk három valós számot. Mekkora annak a valószínűsége, hogy ezek négyzetösszege legfeljebb 1?
|
|
|
| [460] Hajba Károly | 2004-09-02 17:15:48 |
 Kedves László!
> Nem is tudom mire lehetne ez válasz amit beírtam.
Egy zsákba beletettük az összes lehetséges módon kitöltött lottószelvényt. Hány szelvényt kell kihúznunk, hogy biztos legyen ezek között hármas találatú?
Talán erre lenne jó a válaszod. :o)
HK
|
| Előzmény: [456] lorantfy, 2004-09-01 17:50:40 |
|
| [459] V. Dávid | 2004-09-01 21:01:25 |
 Hogy érted, hogy nem lehet-e negatív gyök? Kösz, ha az az egyetlen megoldása, amit én találtam ki, akkor a feladat tényleg nagyon szép. De lehet, hogy valaki talál egy sokkal kézenfekvőbbet.
|
| Előzmény: [458] Káli gúla, 2004-09-01 20:19:31 |
|
|
|
|
| [455] Hajba Károly | 2004-09-01 15:46:40 |
 Kedves Dávid!
Jogos az észrevételed. (Nem figyeltem elég jól, hogy ez is binom-os :o) Tehát első durva közelítésben 2 számpár esetén több, mint 400 szelvényt kellene kitöltenünk.
HK
|
| Előzmény: [454] V. Dávid, 2004-09-01 15:38:33 |
|
|
| [453] Hajba Károly | 2004-09-01 15:35:33 |
 Kedves Káli gúla!
Utána számoltam az egyszerűbb változat egy durva alsó közelítésének. Egy szelvényen 5 szám segítségével 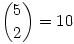 számpár adható meg. Összesen 90*89=8010 számpár lehetséges, így legalább számpár adható meg. Összesen 90*89=8010 számpár lehetséges, így legalább 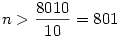 szelvény szükséges a feladat megoldásához. De mivel sok átfedés lehetséges, így ez a szám ennél magasabb. (Tehát feltehetően rosszul emlékeztem :o) szelvény szükséges a feladat megoldásához. De mivel sok átfedés lehetséges, így ez a szám ennél magasabb. (Tehát feltehetően rosszul emlékeztem :o)
Érdekelne a pontos küszöb levezetése is, melyet említettél.
HK
|
| Előzmény: [451] Káli gúla, 2004-09-01 14:58:15 |
|
| [452] V. Dávid | 2004-09-01 15:35:07 |
 Az ilyen "lehetetlennek" látszó feladatokat úgy lehet a lekönnyebben megoldani, hogy felteszed, hogy tényleg megoldhatatlan, és megpróbálod ezt bizonyítani. Egy idő után rájössz, hogy miért nem lehet bizonyítani a megoldhatatlanságát, és ebből indulhatsz ki az eredeti feladat megoldását illetően.
|
| Előzmény: [418] lorytibi, 2004-07-17 20:01:28 |
|
| [451] Káli gúla | 2004-09-01 14:58:15 |
 nem is kell minden lehetséges hármast lefedni ...
Két nagyon egyszerű szűkítés:
(a) Vegyük a páratlan hármasokat és a páros hármasokat, ez összesen 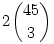 = 28380. = 28380.
(b) Öt szám között van három azonos mod 3, vagy három különböző mod 3, így elég:
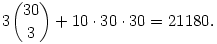
Kedves Károly,
Az "egyszerűbb változat" a kettesekkel egyáltalán nem egyszerű, a pontos küszöb sokáig megoldatlan probléma volt.
|
| Előzmény: [449] V. Dávid, 2004-09-01 13:31:43 |
|
| [450] Hajba Károly | 2004-09-01 14:48:50 |
 Kedves László!
Dávidnak teljesen igaza van. A feladat egyszerűbb esetét tekintve, ha csak egy számot szeretnék mindenképpen eltalálni, elég 18 szelvényt kitölteni, de ha csak 89 szám közül kellene 5-öt húzni, akkor 17 is elég lenne.
Mintha valahol láttam/halottam, hogy 2 számhoz kb. 100 szelvényt kellene megfelelő módon kitölteni. Javaslom, hogy a feladat megoldásához először ezen egyszerűbb változatát próbáljuk megoldani tételes szelvénykitöltéssel együtt.
HK
|
| Előzmény: [448] lorantfy, 2004-09-01 11:54:06 |
|
| [449] V. Dávid | 2004-09-01 13:31:43 |
 Kedves Lorantfy! A feladat lényege, hogy legalább hány lottószelvényre van szükség. A te megoldásod szerint 43913143-ra, ez mindössze 36125-tel kevesebb, mint amennyi a biztos ötöshöz kell. Ennél nyilván sokkal kevesebb is elég. Egy felső becslés: ha minden szelvényen csak egyetlen hármast számítunk, még 117480 is sok. De minden szelvény 10 lehetséges hármast fed le, ráadásul nem is kell minden lehetséges hármast lefedni, csak arra van szükség bármely öt szám közül ki lehessen választani hármat úgy, hogy ez a három szám a valamelyik megjelölt szelvény öt száma közül hárommal egyezzen. Még érdekesebb kérdés, hogy hogyan kell kitölteni a szelvényeket.
|
| Előzmény: [448] lorantfy, 2004-09-01 11:54:06 |
|
| [448] lorantfy | 2004-09-01 11:54:06 |
 94. feladat megoldása: Gondolom a hagyományos 90/5-ös lottóra gondoltál. Kitöltjük azokat a szelvényeket amelyeken nincs találat, majd azokat amelyeken pontosan 1 találat van, majd a pontosan 2 találatosokat és a következő, mindezektől különböző szelvényen már biztosan lesz legalább 3 találat:
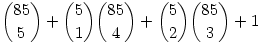
|
| Előzmény: [444] V. Dávid, 2004-08-31 18:58:40 |
|
| [447] V. Dávid | 2004-09-01 10:16:19 |
 Én is üdvözlök mindenkit itt a fórumon. Ezt a feladatot magam találtam ki, és kíváncsi vagyok, hogy milyen gondolkodtatóra sikerült: 95. Feladat: van n darab valós számunk. A k-adik lépésben minden lehetséges módon kiválasztunk ezek közül k-t, ezeket összeszorozzuk, és az így kapott k tényezős szorzatokat összeadjuk. k=1..n (Példa n=3 és k=2-re: x1x2+x1x3+x2x3) Mind az n összeg pozitív. Bizonyítsuk be, hogy a kiindulásul választott összes szám pozitív.
|
|
| [446] lorantfy | 2004-09-01 08:54:19 |
 Kedves Vizi Dávid!
Üdvözöllek a Fórumon és kösz a szellemes megoldást! A forma az nem tetszik! Ha nem haragszol meg érte, gyorsan átírom:
Vezessük be az 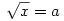 és és 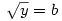 jelöléseket. jelöléseket.
Így az egyenletek:
2a4+b2+2a2+b4=8
a+b=2
Most az egyenlet bal oldalára alkalmazzuk a számtani és a mértani közép közötti egyenlőtlenséget, ebből:
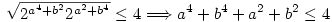
Felhasználva, hogy
a2+b2=(a+b)2-2ab es ÿ(a+b)2=4 2ab 2ab a4+b4 a4+b4
Bevezetjük az a=1-d és b=1+d jelöléseket, ezeket behelyettesítve:
2-2d2 2d4+12d2+2 2d4+12d2+2
azaz 0 2d4+14d2 2d4+14d2
innen már simán látszik, hogy d=0,ezek szerint a=b=1, tehát x=y=1 az egyetlen megoldás.
|
| Előzmény: [445] V. Dávid, 2004-08-31 21:09:49 |
|
| [445] V. Dávid | 2004-08-31 21:09:49 |
 Bocsánat, de most regisztráltam, úgyhogy még nem volt lelkierőm végig csinálni ezt a TeX tanfolyamot. Jobb híján a ? a hatványozás jele. A 93-as megoldása: Vezessük be az sqrt(x)=a és sqrt(y)=b jelöléseket. Így az első egyenlet: 2?(a?4+b?2)+2?(a?2+b?4)=8 Most az egyenlet bal oldalára alkalmazzuk a számtani és a mértani közép közötti egyenlőtlenséget, ebből: 4>=a?4+b?4+a?2+b?2 Felhasználva, hogy a?2+b?2=(a+b)?2-2ab 2ab>=a?4+b?4 Bevezetjük az a=1-d és b=1+d jelöléseket, ezeket behelyettesítve: 2-2d?2>=2d?4+12d?2+2, azaz 0>=2d?4+14d?2, innen már simán látszik, hogy d=0, ezek szerint a=b=1, tehát x=y=1 az egyetlen megoldás.
|
| Előzmény: [442] lorantfy, 2004-08-19 17:11:05 |
|
| [444] V. Dávid | 2004-08-31 18:58:40 |
 94. Feladat: Legalább hány lottószelvényt kell kitölteni ahhoz, hogy biztosan legyen hármas találatunk?
|
|
| [443] V. Dávid | 2004-08-31 17:52:32 |
 "Mi a helyzet akkor, ha nincsen kalapjuk meg kavicsuk, csak papíruk és ceruzájuk?" Ugyanaz a helyzet mint akkor, amikor kavicsokat dobáltak. Mondjuk 1. annyi szakaszt húz, ahány éves, aztán behajtja a lapot. 2. pedig itt folytatja a vonalhúzogatást. A lap visszahajtása után a szakaszok határa nem látható. (Feltesszük, hogy eközben más nem néz a lapra.)
|
| Előzmény: [425] Csimby, 2004-07-20 00:58:53 |
|
|
| [441] lorantfy | 2004-08-19 17:05:54 |
 93.feladat: Oldjuk meg az egyenletrendszert!
2x2+y+2x+y2=8
sqrtx+sqrty=2
|
|
|
| [439] joe | 2004-08-07 18:11:07 |
 92. feladat: Van két piros, két fehér és két zöld golyónk. Az azonos színűek közül az egyik 100, a másik 101 grammos. Egy kétkarú mérleg segítségével, mérősúlyok nélkül, két méréssel állapítsuk meg mindegyik golyó súlyát!
|
|
| [438] Káli gúla | 2004-08-05 23:06:09 |
 Sziasztok!
Megoldás a 71. feladatra.
Színezzük pirossal és kékkel a sakktáblát. Elég belátni, hogy vagy (a) van minden oszlopot érintő piros út, vagy (b) van minden sort érintő kék út, mert (a) esetben a piros, (b) esetben a kék rész járható végig.
Nyilván feltehetjük, hogy nincsen sem egyszínű sor, sem egyszínű oszlop. Ha bármelyik két szomszédos oszlopnál a piros mezők közt van valahol "átjárás", akkor az (a) eset teljesül, ezért feltehetjük, hogy az i-edik oszlop piros mezőiről nincs átjárás az (i+1)-edik oszlop piros mezőire. Ekkor ez a két oszlop tartalmazni fog egy (b) szerinti kék utat, mert egyrészt az i-edik oszlop piros pontjai mellett az (i+1)-edik oszlopban kék pontok vannak, tehát a két oszlop kék színű pontjai az összes sort lefogják, másrészt az i-edik oszlop nem egyszínű, így valamelyik piros mezőjének van függőleges kék szomszédja is, ami a vízszintes kék szomszédjával átlósan összeköthető.
|
|
| [437] Suhanc | 2004-08-02 13:00:22 |
 Kedves Csimby!
Bocsi, hogy ilyen "jó" a reakcióidőm... táborozni voltam. A négy dimenziós kockának csak a megoldását tudom, a füzetemet meg még nem találtam meg, amibe leírtam!;)
De keresem...:)
A Gordiuszon mesélte egy srác, hogy a sulijában páran összefogva elemezték a SET-et, olyan k és l paraméterekre, hogy k a tulajdonságok száma, l egy tulajdonságon belül a lehetőségek száma. Erre is sikerült asszem megadniuk a maximális húzható lapot...
A fodrászos feladathoz pedig 2 dolog jutott eszembe:
1. Egy másik megoldásötlet: Hívjuk vissza Gedeon bácsit, de előtte a három nő beszéljen meg egy X számot! Majd egyenként mondják meg neki életkor +X értékét. Ekkor Gedeon bácsi tudja a sorrendet, de nem tudja a valós életkort!:)
2. Egy kérdés: Összejátszhat-e bármely 2 nő a harmadik életkorának megismeréséért? / szóval kibeszélik-e;)) / Mert, ha feladatod azt kéri, még öszejátszással se lehessen kideríteni, akkor az eddigi két ötletem nem volt jó...:)
|
| Előzmény: [436] Csimby, 2004-07-23 18:36:33 |
|
| [436] Csimby | 2004-07-23 18:36:33 |
 Helló!
Én is ott voltam a táborban, de erre sajnos nem emlékszem ;-( így érdemes engem tanítani. Na de most én is a SET kapcsán kezdtem el ezzel foglalkozni! A max. már megvan általánosan csak bizonyítani még nem sikerült, a SET-re sem(SET-nél 4 dimenziós kocka kell)(négyzetre megvan), de már érzem, hogy meglessz a SET is :-) Ha emlékszel vmire amit a táborban mondtak róla légyszi írd meg (csajbok@dpg.hu)! Nagyon jó az a játék és érdekes problémákat vet fel...
|
| Előzmény: [434] Suhanc, 2004-07-23 13:31:28 |
|
| [435] Suhanc | 2004-07-23 13:46:42 |
 Egy ötlet a 90.Feladat-hoz:
Legyen a három nő 1. 2. 3., életkoruk A;B;C. 1. gondol egy pozitív egész X számra, és megsúgja 2.-nek az A+X összeget. 2. megsúgja 3.-nak az A+B+X összeget. 3. megsúgja 1.-nek az A+B+C+X összeget.
Ekkor 1. Ismeri B+C+X értékét. Megsúgja 2.-nak a B+C+X összeget. Mivel 2. Ismeri saját életkorát, így ismeri C+X összeget.
Mivel 2. ismeri A+X és C+X összegeket, így ismeri C-A értékét. E különbség előjele meghatározza, hogy A vagy C az idősebb. Ezt B hangosan bemondja.
Ezután B, majd C gondol egy számot,és így 3kör alatt három egyenlőtlenséghez jutunk, melyekben az életkorok szerepelnek, és így egyértelműen meg tudjuk állapítani a sorrendet.
Megj. ez a megoldás csak akkor működhet, haténylegnem egyidősek... de ha mondjuk pontosítunk, és A= 10000000000000000000000000*8születési év)+1000000000*(születés hónapja)+100000*(nap) +1000*(óra)+(perc) B=...
akkor nagy valószínűséggel nem lesz A=C ;)
Egy extrémebb kérdés, bár nem gondoltam át, hogy van-e egyáltalán megoldása...
Mindhárman a búra alatt ülnek, és ordibálnak... tehát nincs suttogás, mindenki hall mindent, se papír, se toll! most mit lehet csinálni?
|
|
| [434] Suhanc | 2004-07-23 13:31:28 |
 Kedves Csimby!
Ezzel a feladattal a tavalyi Montágh- Hraskó-Kós féle táborban talákoztam, a SET nevű játék kapcsán. :)
Akkor ott ezt 3D-ben, és az eredeti játékra vonatkozóan is vizsgálta az előadó...
|
|
| [433] Csimby | 2004-07-23 12:12:10 |
 Elnézést, nem voltam elég világos, tehát átlónak tekintem pl. a következő ábrán mind a 3 különböző színnel jelölt 3-as csoportot.
|
 |
|
| [432] Sirpi | 2004-07-23 11:36:29 |
 Bocs, nem olvastam el a feladat legutolsó mondatát... Szóval nxn-es esetben mind a 2n átlót kéne figyelni, szóval rossz, amit írtam.
Ebéd alatt majd kitalálom :-)
|
| Előzmény: [431] Sirpi, 2004-07-23 09:29:27 |
|
| [431] Sirpi | 2004-07-23 09:29:27 |
 Ez megy nxn-esre is, ha n 3, azaz be lehet bizonyítani, hogy n(n-1) a maximum (több nem lehet, mert akkor a skatulyaelv miatt lenne teli sor). 3, azaz be lehet bizonyítani, hogy n(n-1) a maximum (több nem lehet, mert akkor a skatulyaelv miatt lenne teli sor).
Vázlat:
o+++++++
++++++o+
+++++o++
++++o+++
+++o++++
++o+++++
+o++++++
+++++++o
Mj: n=1-re 0, n=2-re 1 a maximum.
|
| Előzmény: [429] Csimby, 2004-07-23 00:19:20 |
|
| [430] Suhanc | 2004-07-23 08:54:47 |
 Kedves Csimby!
A 91. Feladat-ot nem értem...
/így jártam;) /
Az nem világos, hogy miért emeled ki a nem főátlókat, hiszen azokban nincs 3 mező, értelemszerűen nem is tudunk majd ott 3-at kiválasztani.
Ha a feladat tényleg így szól, azt hiszem, ez egy lehetséges megoldás:
Tekintsük a négyzet sorait! Minden sorban legfeljebb 2 kiválasztott négyzet lehet, tehát legfeljebb 6- ot választhatunk ki. 6-ra pedig készíthető ilyen konstrukció:
Ha megszámozzuk a 9 mezőt a számológépek klaviatúrájának megfelelően (bocsánat, rajzolni még most sem tudok) , akkor válasszuk ki a 2,3,4,6,7,8 mezőket.
Ekkor minden sorban és oszlopban , valamint az egyik főátlóban 2 kiválasztott mező van, míg a másik főátló üres.
|
| Előzmény: [429] Csimby, 2004-07-23 00:19:20 |
|
| [429] Csimby | 2004-07-23 00:19:20 |
 91.feladat Ez nem nehéz, csak arra vagyok kíváncsi, hogy ki hogyan bizonyítja:
Van egy 3×3-as négyzetünk. Legfeljebb hány mezőt tudunk úgy kiválasztani, hogy semelyik oszlopban, sorban és átlóban se legyen 3 a kiválasztott mezők közül (átló alatt nem csak a két fő átlót, hanem mind a 6-ot értem).
|
|
| [428] Csimby | 2004-07-21 15:40:07 |
 Igazad van, pl. A nem tudhatja meg A és B vagy A és C kor különbségét. Az összehasonlítást tehát vagy úgy kell elvégezni, hogy csak az derüljön ki melyik az idősebb ne az, hogy mennyivel. Vagy pedig ha pl. A és B korkülönbségét akarjuk megtudni, akkor azt C vizsgálja (ő megtudhatja mennyi a különbség, konkrét infója ebből neki nem lesz és nem árulja el csak azt, hogy ki az idősebb), persze C+A-t és C+B-t nem hasonlíthatja össze C, hiszen akkor megtudná A és B korát. Az egyenlőséget egyébként kizárhatjuk, ha a korhoz hozzávesszük, a hónapot, napot, percet.
|
| Előzmény: [427] Sirpi, 2004-07-21 13:23:30 |
|
| [427] Sirpi | 2004-07-21 13:23:30 |
 Nem kötözködésből, csak érdekel:
Arról volt szó, hogy úgy akarják meghatározni az életkor sorrendet, hogy a másik két hölgy számára ne derüljön ki semmilyen információ a tényleges korukról. Igazából a korok nem is mindig derülnek ki, de mindenki tudni fogja, hogy hány év korkülönbség van a másik kettő között. Wz ezért plusz információ a sorrendhez képest. Azért megengedjük?
(Példa: kiderül, hogy az első hölgy a legidősebb, és a másik kettő pedig megegyező korú. Ekkor mind a hárman explicite tudni fogják az életkorokat is.)
|
|
| [426] Hajba Károly | 2004-07-20 16:39:38 |
 Kedves Csimby!
Te még korodnál fogva nem ismerheted Gedeon bácsi főhajszobrászt, a nők bálványát, de benne minden nő megbízik és két dajer között mindhárom nő a fülébe súgja a korát és ő sorba rakja őket. :o)
Nos, ha a papírra vetett számokat vagy egyéb információhordozót más nem nézheti meg, csak ők, akkor egyelőre még nem tudom az eljárást. De még gondolkozom rajta egy kicsit.
Üdv: HK
|
| Előzmény: [425] Csimby, 2004-07-20 00:58:53 |
|
|
| [424] Hajba Károly | 2004-07-19 23:55:42 |
 Megpróbálom egy kicsit egzaktabbul előadni a feladatmegoldásomat, s ellenézést a slendriánságért. :o)
Legyen a 3 nő életkora A, B, C és rendre összehasonlítják a következők szerint. 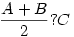 ; ; ; ;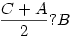 . .
A ? jel helyén <,>,= relációk lehetségesek, így összesen 27 féle eredmény képzelhető el, de ebből 14 féle állapot kizárt.
Egyik valós állapot, mikor mindhárom egyenlő, ekkor egyforma idősek. Ezenkivül már csak olyan állapot lehetséges, mikor legalább egy > és legalább egy < jel is szerepel. Az a nő, ki egyedül kisebb vagy egyedül nagyobb, egyúttal a hármójuk közül a legfiatalabb ill. legidősebb is. A másik kettő ilyenkor úgy tudja eldönteni a sorrendet, hogy megnézik a harmadikkal együtt az övék több vagy a másik. Pl. ha A már ismert akkor (A+B)?(A+C). Ezek az értékek már egyébként is ismertek.
Előfordul olyan állapot is, mikor egy legkisebb és egy legnagyobb adódik egyszerre, ekkor a harmadik egyenlő, s ebből logikusan következik a sorrend is. Pl. 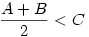 ; ;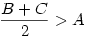 ; ;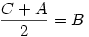 . Ekkor a sorrend A<B<C. . Ekkor a sorrend A<B<C.
HK
|
| Előzmény: [423] Csimby, 2004-07-19 22:31:52 |
|
| [423] Csimby | 2004-07-19 22:31:52 |
 "Ha két ilyen is van, akkor az egyik kisebb, a másik nagyobb, a harmadik egyenlő." - Egyenlő mivel?
"A két egyformán kisebb vagy nagyobb kettő megnézi, hogy az előbbivel együtt több vagy kevesebb kaviccsal rendelkeznek, s ebből következtethetnek a koruk viszonyára." - Mi az előbbi?
Bocsánat, nem csak kötözködés, tényleg nem értem.
|
| Előzmény: [422] Hajba Károly, 2004-07-19 18:40:30 |
|
| [422] Hajba Károly | 2004-07-19 18:40:30 |
 a 90. feladathoz:
Mindhárom nő párosával annyi kavicsot dob egy kalapba ahány éves, s a harmadik megnézi, hogy a kalapban lévő kavicsok felénél az ő kora kevesebb, több vagy egyenlő. Így három vizsgálatot végeztek.
Aki kora egyedül kevesebb vagy több a kalapban lévő kavicsok felénél, az a legfiatalabb vagy legidősebb. Ha két ilyen is van, akkor az egyik kisebb, a másik nagyobb, a harmadik egyenlő. Ebből már adódik a sorrend.
A két egyformán kisebb vagy nagyobb kettő megnézi, hogy az előbbivel együtt több vagy kevesebb kaviccsal rendelkeznek, s ebből következtethetnek a koruk viszonyára. Akár egyidősek is lehetnek.
Meg egy lehetőség adódik, amikor mindhárom eset egyenlőt ad. Ekkor egyenlő korúak.
A három mérésből elvileg 27 féle lehetséges kimenet lehet, de ebből 14 féle lehetetlen.
Üdv: HK
|
| Előzmény: [421] Csimby, 2004-07-19 13:05:08 |
|
| [421] Csimby | 2004-07-19 13:05:08 |
 Még régebben mondta egy barátom, aznap amikor egy orvosi vizsgálat miatt 1/2 órát kellett mozdulatlanul feküdnöm. Mire vége lett megvolt :-). Mikor feladtad, a megoldásra már nem emlékeztem csak arra, hogy egyszer már megcsináltam. Bocsánat, hogy ilyen gyorsan lelőttem, pedig már ismertem, de ez az egyik kedvenc példám!
90.feladat A fodrásznál ül 3 nő és szeretnék egymást koruk szerint növekvő sorrendbe rendezni. Ugyanakkor egyik sem szeretné, hogy a sorrenden kívül bármilyen információ is kiderüljön a koráról, a végén tehát semmit sem fognak tudni a másik életkoráról csak az életkoruk sorrendjét. Hogyan csinálják?
|
| Előzmény: [420] lorytibi, 2004-07-19 11:12:08 |
|
| [420] lorytibi | 2004-07-19 11:12:08 |
 Ez szép volt Csimby!
Ismerted a feladatot, vagy csak ilyen könnyű volt?
Nekem nagyon nehéznek tűnt, nem gondoltam volna, hogy egy ilyen egyszerű trükkel meg lehet oldani.
|
| Előzmény: [419] Csimby, 2004-07-19 00:43:26 |
|
| [419] Csimby | 2004-07-19 00:43:26 |
 Kiválasztassz 100-at tetszőlegesen és megfordítod! Ez a 100 db. lesz az egyik csoport a másik pedig az összes többi. Bővebb indoklást direkt nem írok, gondoljátok végig!
|
| Előzmény: [418] lorytibi, 2004-07-17 20:01:28 |
|
| [418] lorytibi | 2004-07-17 20:01:28 |
 Na, ez a jól elgondolkodtató feladat után feladok egy másikat, amit ugyancsak az egyik tanárom edott fel a zalai matektáborban:
89.feladat: Egy asztal előt ülsz bekötött szemmel, az asztalon korongok vannak, amelyeknek egyik oldala kék, a másik meg piros. 100 darab korongnak a piros oldala van fölül, a többinek a kék. Oszd két csoportba a korongokat úgy, hogy a csoportokban ugyanannyi piros(piros része látszik) korong legyen!
- Kitapogathatod, hogy hány korong van, így megtudhatod hány kék.
- Meglehet fordítani őket, (de szerintem azt úgy lenne érdemes, ha az összeset egyszerre megfordítjuk,) hisz, ha csak egyet fordítasz, nem tudhatjuk milyen színű.
Sajnos ennek a feladatnak nem tudom a megoldását, elégé megoldhatatlannak tűnik. Várom a próbálkozásokat!
|
|




 R+ folytonos függvény, amelyre g(g(x))=1/x minden x
R+ folytonos függvény, amelyre g(g(x))=1/x minden x R+-ra.
R+-ra.


 egy primitív nyolcadik egységgyök, ekkor
egy primitív nyolcadik egységgyök, ekkor 
 nem más, mint
nem más, mint 
 1 mod 5), de mivel mindegyik prím, ezért p1-nek 1 maradékot kell 5-tel osztva adnia. Ekkor p1 6-ra vagy 1-re végződik, 6-ost ki zárhatjuk, mert p1 páratlan kell, hogy legyen.
1 mod 5), de mivel mindegyik prím, ezért p1-nek 1 maradékot kell 5-tel osztva adnia. Ekkor p1 6-ra vagy 1-re végződik, 6-ost ki zárhatjuk, mert p1 páratlan kell, hogy legyen.

 helyettesíti, mivel nem találtam megfelelőbbet.
helyettesíti, mivel nem találtam megfelelőbbet.  2 természetes számra
2 természetes számra  Q2
Q2 1 és l
1 és l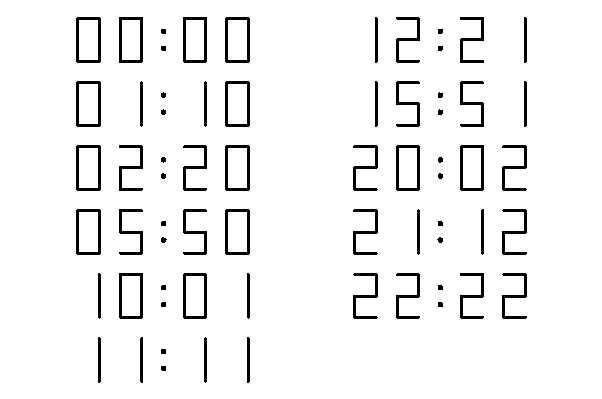






 -t.
-t.




 2ab
2ab
