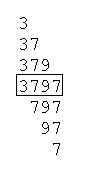|
| [2234] Cckek | 2007-08-23 14:12:01 |
 Most épp Csebisev polinomokkal foglalkozgatom, tahát Tn(x)=cos (narccosx) polinom. Mi a helyzet forditva? arccos(ncos x) hogyan néz ki? Vagy általánosan melyek azok a bijektív függvények melyekre
f(n.f-1(x)) polinom?
|
|
| [2235] HoA | 2007-08-23 17:00:28 |
 Úgy látom, Gyöngyő nem érti, mennyire jogos Csimby felvetése. Szerintem a feladatot valahogy úgy kéne megfogalmazni: Mi az a minimális fogalom, definíció, axióma halmaz, amiből adódik, mit jelent a "0", az "1" és a ">" , és amiből be lehet bizonyítani az állítást? Úgy sejtem, a teljesen rendezett kommutatív test fogalmára nincs szükség.
|
| Előzmény: [2232] Gyöngyő, 2007-08-23 12:30:27 |
|
| [2236] Lóczi Lajos | 2007-08-23 18:31:13 |
 A teljességre valóban nincs szükség.
A felvetésednek mindazonáltal nem igazán látom értelmét: legyen összesen 2 elemünk, és egy ">"-gyel jelölt reláció. Az egyetlen igaz állítás (axióma) a rendszerünkben pedig legyen az, hogy "1>0". A jelek jelentését firtatni itt értelmetlen. :)
|
| Előzmény: [2235] HoA, 2007-08-23 17:00:28 |
|
|
| [2238] Csimby | 2007-08-23 21:48:33 |
 Szerintem, ha ennyire lemegyünk, az alapokig, hogy 1>0, akkor tisztáznunk kell a definíciókat, hogy tudjuk mit használhatunk a bizonyítás során. Nem gondoltam utána, de nem vagyok benne biztos, hogy pl. CCkek bizonyítása nem használja-e fel valahol, hogy 1>0.
|
| Előzmény: [2236] Lóczi Lajos, 2007-08-23 18:31:13 |
|
| [2239] Sirpi | 2007-08-23 21:56:59 |
 Azt, hogy a fv. hol vesz fel racionális értékeket, szerintem se érdemes túlzottan vizsgálni. Annyi bizonyos, hogy a folytonosság miatt a minimuma és maximuma között felveszi az összeset.
Már az x3-x fv.-ről se látom kapásból, hogy milyen irracionális értékekra racionális (ehhez az x3-x-p/q=0 harmadfokú egyenletet kell megoldani mindenféle p,q értékekre).
|
| Előzmény: [2226] Cckek, 2007-08-22 12:21:54 |
|
|
| [2241] Lóczi Lajos | 2007-08-23 23:22:24 |
 Ha az eredeti kérdés a valós számok szokásos axiómarendszerére vonatkozik, akkor egy lehetséges válasz a következő.
Az 1/6-os axióma szerint létezik egy (-1)-gyel jelölt elem, ami az 1 additív inverze. Nézzük, mennyi (-1)(-1). Azt állítom, hogy 1. Az additív inverz egyértelműsége miatt (tessék igazolni az axiómákból!) ehhez elég megmutatni, hogy (-1)(-1)+(-1)=0. Az 1/5-ös axióma miatt a bal oldal= (-1)(-1)+(-1).1, az 1/3-as axióma miatt viszont ez =(-1)[(-1)+1]=(-1).0, a (-1) definíciója miatt. Most igazolom, hogy minden valós x-re x.0=0. Nézzük az x.0+x.0 kifejezést. Az 1/3-as axióma miatt ez utóbbi = x.(0+0)=x.0, az 1/4-es axióma miatt. Tehát x.0+x.0=x.0. Most adjuk hozzá mindkét oldalhoz a -(x.0) számot, azaz az 1/6-os miatt létező additív inverzét x.0-nak. Azt kapjuk, hogy x.0=0, az additív inverz definíciója miatt. Speciálisan: (-1).0=0 és ezzel beláttam, hogy (-1)(-1)=1.
Most érdemes belátni (tessék igazolni az axiómákból!), hogy egy x elem (-x) additív inverze ugyanaz, mint (-1).x. Ezután az 1/2-es miatt kapjuk, hogy x.x=(-x).(-x).
Most lássuk be azt, ha x 0, akkor az additív inverzre fordított reláció áll fenn. Valóban: 0=x+(-x) 0, akkor az additív inverzre fordított reláció áll fenn. Valóban: 0=x+(-x) (-x) a 3/1-es és a (-x) a 3/1-es és a  tranzitivitása miatt. tranzitivitása miatt.
Most megmutatom, hogy akármilyen x valós elemre x.x 0. Két eset van (melyik axióma miatt?). Ha x 0. Két eset van (melyik axióma miatt?). Ha x 0, akkor x.x 0, akkor x.x 0 igaz a 3/2-es miatt. Ha x 0 igaz a 3/2-es miatt. Ha x 0, akkor a fentiek alapján x.x=(-x)(-x) és most 3/2-es axióma. 0, akkor a fentiek alapján x.x=(-x)(-x) és most 3/2-es axióma.
Viszont ekkor 1.1 0 is teljesül. De 1/5-ös szerint 1=1.1, tehát 1 0 is teljesül. De 1/5-ös szerint 1=1.1, tehát 1 0. Viszont tudjuk 1/5 alapján, hogy 1 0. Viszont tudjuk 1/5 alapján, hogy 1 0, így a > definíciója miatt 1>0. 0, így a > definíciója miatt 1>0.
Jó játék, nem? :-)
Esetleg tudna valaki lényeges rövidítést adni a fenti axiómaszámozást használva?
|
| Előzmény: [2238] Csimby, 2007-08-23 21:48:33 |
|
| [2242] Csimby | 2007-08-24 10:15:23 |
 Hogy mi "szokásos" és mi nem, az sztem attól függ, hogy hol vagyunk :-). Gimnáziumban például amikor elkezdtünk arról beszélni, hogy Q és akkor ez test és két művelet +, * stb. Akkor "a>b"-t úgy definiáltuk, hogy "a>b" acsa. ha a-b Pozitív. (Nincsen akkor-és-csak-akkor nyíl?) Ahol a Pozitív halmaz halmaz definíciójára már nem emlékszem, de talán lehet azon Q-beliek halmaza melyek előállnak (1+1+...+1)/(1+1+...+1) alakban. Ez nyilván működik Z-ben is. Hogy R-ben ezt hogy lehetne megoldani, azt nem tudom, lehet hogy nem is lehet. És ha így definiáltuk, akkor 1>0-n nincs mit bizonyítani. Persze elegánsabb és számomra nagyon tanulságos volt amit te írtál, hogy, felvesszük a rendezés axiómáit is és azt mondjuk, hogy a>b acsa. a Pozitív. (Nincsen akkor-és-csak-akkor nyíl?) Ahol a Pozitív halmaz halmaz definíciójára már nem emlékszem, de talán lehet azon Q-beliek halmaza melyek előállnak (1+1+...+1)/(1+1+...+1) alakban. Ez nyilván működik Z-ben is. Hogy R-ben ezt hogy lehetne megoldani, azt nem tudom, lehet hogy nem is lehet. És ha így definiáltuk, akkor 1>0-n nincs mit bizonyítani. Persze elegánsabb és számomra nagyon tanulságos volt amit te írtál, hogy, felvesszük a rendezés axiómáit is és azt mondjuk, hogy a>b acsa. a b és a b és a b, de pl. a gimiben, noha a többi axióma szerepelt nálunk (igaz, talán csak Z-re) a rendezés axiómái kimaradtak és ezt a fent leírt módon oldottuk meg. b, de pl. a gimiben, noha a többi axióma szerepelt nálunk (igaz, talán csak Z-re) a rendezés axiómái kimaradtak és ezt a fent leírt módon oldottuk meg.
|
| Előzmény: [2241] Lóczi Lajos, 2007-08-23 23:22:24 |
|
| [2243] ilozagrav | 2007-08-24 13:40:44 |
 Sziasztok!
Két halmaz ekvivalens akkor és csak akkor, ha létezik közöttük bijekció. Bizonyítható hogy ez tényleg ekvivalenciareláció. Egy f operációt kompatibilisnek mondunk egy ekvivalenciarelációval ha
f(A) = f(B) <=> A ekvivalens B - vel
Adjunk meg olyan operációt amely kompatibilis a halmazokon értelmezett ekvivalenciával, azaz tegyük lehetővé a számosság matematikai értelmezését!
Várom az ötleteket üdv.Zoli
|
|
|
| [2245] ilozagrav | 2007-08-24 14:14:31 |
 Szia!
Én kreatív ötleteket várok.Egyébként egy normális halmazelmélet könyvben le van írva a válasz: Egy A halmaz számossága a legkisebb A-val ekvivalens rendszám. A kérdés az lenne inkább hogy találunk-e ilyen operációkat ami az előzőből nem triviálisan keletkezik.
|
| Előzmény: [2244] jonas, 2007-08-24 13:56:56 |
|
|
| [2247] Q | 2007-08-25 21:33:53 |
 Sziasztok! Tudtok valami érdekes feladatot rekurzív sorozatokkal kapcsolatban? Órai előadáshoz kéne.
|
|
| [2248] ilozagrav | 2007-08-25 21:48:28 |
 Szia!
Pl. Pell egyenlet és másodrendű rekurzív sorozatok kapcsolata, elmehetsz a vektorterek irányába is,számtalan dolog lehet.Fibonacci sorozat stb.Nagy az irodalma üdv Zoli
|
| Előzmény: [2247] Q, 2007-08-25 21:33:53 |
|
|
|
| [2251] Lóczi Lajos | 2007-08-26 00:53:37 |
 Ebben a topikban több érdekes, rekurzióval kapcsolatos feladatot (és megoldást) találsz. (Javaslom, állítsd 200-ra a megjelenített hozzászólások számát és akkor elég hamar megtalálod az összeset.)
|
| Előzmény: [2247] Q, 2007-08-25 21:33:53 |
|
| [2252] Lóczi Lajos | 2007-08-26 00:57:11 |
 De a http://mathworld.wolfram.com/NewtonsIteration.html és http://mathworld.wolfram.com/LogisticMap.html oldalak igazi gyöngyszemek, amelyekből nemhogy órai előadást, de egész éves kurzust lehet tartani...
|
| Előzmény: [2251] Lóczi Lajos, 2007-08-26 00:53:37 |
|
| [2253] Q | 2007-08-26 09:25:09 |
 Köszi mindenkinek, rajta vagyok.
|
|
| [2254] ilozagrav | 2007-08-26 21:30:33 |
 Sziasztok!
Komplex elemű mátrix főátlón kívüli elemeit rögzítjük. Bizonyítsuk be, hogy megválaszthatók a főátlóbeli elemek úgy, hogy a mátrix sajátértékei előre adottak,és hogy a mátrix sajátértékei az adott értékek legyenek.
|
|
| [2255] rizsesz | 2007-09-02 20:52:05 |
 Helló! Nem tudom, hogy hanyadik feladat sajna, de itt a szöveg:
Egy kocka 3 kitérő élétől egyenlő távolságra levő pontok halmaza micsoda?
|
|
| [2256] HoA | 2007-09-03 15:25:28 |
 Kérdések:
a) a 3 kitérő él úgy értendő, hogy 3 különböző irányú? b) egy éltől adott távolságra lévő pontok halmaza végtelen henger vagy két félgömbbel lezárt véges henger?
|
| Előzmény: [2255] rizsesz, 2007-09-02 20:52:05 |
|
| [2257] rizsesz | 2007-09-03 16:40:14 |
 a., a 3 kitérő él azt jelenti, hogy 3 közös ponttal nem rendelkező élre gondolok. ha a hagyományos kockavázat nézzük, akkor egy él alulról, egy oldalsó él és egy felülről, úgy, hogy semelyik két élhez nem tartozik közös csúcs; forgatással és tükrözéssel egybevágóság erejéig egy ilyen élhármas létezik.
b., igazából véges henger, olyan értelemben, hogy megoldást a kocka síkjában keresünk.
|
| Előzmény: [2256] HoA, 2007-09-03 15:25:28 |
|
| [2258] Doom | 2007-09-03 16:40:54 |
 3 kitérő él: semelyik 2 nem metsző és semelyik 2 nem párhuzamos (pl. az egy csúcsból induló 3 él NEM kitérő, pedig különböző irányúak).
|
| Előzmény: [2256] HoA, 2007-09-03 15:25:28 |
|
| [2259] parizsi | 2007-09-04 17:59:51 |
 szeretném a nagyérdemű segítségét kérni az alábbi feladat megoldásához:XI + XXX = X egy gyufaszálat lehet elmozdítani a feladat megoldásához.
|
|
| [2260] Yegreg | 2007-09-04 18:20:14 |
 Szerintem a legelegánsabb megoldás pl. a X+XXX X :oD X :oD
Ha megengedjük a "ferde" egyest, akkor -XI+XXI=X. Jobb ötletem most nincs.
|
|
|
|
|
|
| [2265] Cckek | 2007-09-05 16:08:11 |
 Ez azt hiszem valós elemű mátrix esetén is igaz amennyiben az diagonizálható, az-az n darab különböző sajátértékkel rendelkezik. Legalábbis ezt a Jordan féle kanonikus alakból be tudom bizonyítani. A legnagyobb probléma akkor van ha vannak többszörös sajátértékek. Jó úton haladok???
|
| Előzmény: [2254] ilozagrav, 2007-08-26 21:30:33 |
|
| [2266] Cckek | 2007-09-10 22:53:29 |
 Nagyon sajnálom ezt a feladatom itt kitűzni, ám legyen:) Adott n darab nemegyenlőközű párhuzamos (nyaláb) a térben. Legkevesebb hány párhuzamost (m darab, m=f(n)) kell húzni hozzájuk, hogy egyenlőközű párhuzamosokat (nyalábot) kapjunk?
|
|
| [2267] Lbandi | 2007-09-12 19:47:24 |
 Bizonyítsuk be, hogy az 1pi, 2pi, 3pi ... , 11pi számok között van két olyan, mely végtelen sok számjegyben megegyezik.
|
|
| [2268] rizsesz | 2007-09-12 19:57:31 |
 a skatulya-elv alapján minden helyiértékhez létezik legalább 2 olyan szám a 11 közül, amelyekre igaz, hogy az adott helyiértéken ugyanaz a szám áll. mivel végtelen sok helyiérték van, és a 11 szám közül véges sokféleképpen lehet kettőt kiválasztani (55 módon), ezért ha bármelyik 2 számhoz hozzárendeljük az egyező helyiértékek számát, akkor ezek egyinkének végtelennek kell lennie, lévén az összes egyezések száma végtelen.
|
|
| [2269] Csimby | 2007-09-12 22:29:10 |
 Szia!
Lehet, hogy nem jól értem a feladatot, de pl., ha n=3 és az egyenesek a következőek: (z=0,x=0); (z=0,x=1); 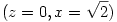 , akkor véges sok egyenessel nem lehet megoldani, hiszen ha az egyenlőközű párhuzamosok távolsága: L, akkor egyrészt 1=kL másrészt , akkor véges sok egyenessel nem lehet megoldani, hiszen ha az egyenlőközű párhuzamosok távolsága: L, akkor egyrészt 1=kL másrészt 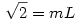 ahol n és m poz. egész, tehát L egyrészt rac. másrészt irrac. kell, hogy legyen. Meg azt sem értem, hogy mit jelent az, hogy egyenlőközű ha az egyenesek nem esnek egy síkba, csak mert 3-nál több párhuzamost nem tudsz úgy elhelyezni a térben, hogy bármely 2 ugyanakkora távolságra legyen egymástól. (Síkban gondolom azt jelenti, hogy egymás után mindig ugyanakkora távolságra következnek, de térben mi a sorrend?) ahol n és m poz. egész, tehát L egyrészt rac. másrészt irrac. kell, hogy legyen. Meg azt sem értem, hogy mit jelent az, hogy egyenlőközű ha az egyenesek nem esnek egy síkba, csak mert 3-nál több párhuzamost nem tudsz úgy elhelyezni a térben, hogy bármely 2 ugyanakkora távolságra legyen egymástól. (Síkban gondolom azt jelenti, hogy egymás után mindig ugyanakkora távolságra következnek, de térben mi a sorrend?)
|
| Előzmény: [2266] Cckek, 2007-09-10 22:53:29 |
|
| [2270] Sirpi | 2007-09-13 09:53:56 |
 Igen, ezt már én is végiggondoltam, és szerintem a kérdés úgy értelmes, hogy a sorrendet Te állíthatod fel, és az egymás utániaknak kell azonos távolságra lenniük. Egyébként nem teljesen világos, hogy miért kell ehhez térbe kimenni, ugyanis, ha veszünk egy, az egyenesekre párhuzamos síkmetszetet, akkor azt a feladatot kapjuk, hogy van néhány nem egyenlő távolságú pontunk a síkban, legkevesebb hány pontot kell felvennünk úgy, hogy egyenlő távolságúakat kapjunk.
Magyarul mi az a legszerencsésebb konfiguráció, amit kevés ponttal is "ki tudunk javítani". Ami még nem teljesen világos, hogy a nemegyenlőközű azt jelenti, hogy a rendezés szerinti sorrendben nem fordul elő az egymás utániak között két egyforma távolság, vagy semelyik két távolság nem azonos (bár az előbbi értelmezés szerint elég lehet akár egyetlen pontot is beszúrnunk, szóval ez nem tűnik túl logikusnak).
Meg ami még kérdés, hogy ha tényleg jól értelmezem, akkor záródnia kell-e a körnek a végén, tehát az első és utolsó közt is a megfelelő távolságnak kell-e lennie, vagy ez nem szükséges?
És bocs, ha totál félreértettem az egészet, de abból a 2 szűkszavú sorból, amit olvastam, nekem ezt sikerült összeraknom.
|
| Előzmény: [2269] Csimby, 2007-09-12 22:29:10 |
|
| [2271] Lóczi Lajos | 2007-09-16 19:53:51 |
 Van-e olyan n pozitív egész, hogy n
a.) valódi osztója J(n)-nek?
b.) valódi többszöröse J(n)-nek?
(A feladatban J(n) azt a pozitív egészt jelöli, amely n-ből úgy keletkezik, hogy annak utolsó számjegyét az első helyre mozgatjuk át. Nullával nem kezdődnek számok.)
|
|
|
| [2273] jonas | 2007-09-17 13:00:51 |
 Tévedtem, mégis van ilyen szám. Korábban vagy nem jól kerestem, vagy csak túl kicsi számok között. A legkisebb ilyen szám az (a) esetben 102564, mivel 4.102564=410256, a (b) esetben pedig 428571, mivel 428571=3.142857. Az utóbbira rá is kellett volna jönnöm, hiszen mindenki tudja, hogy ezek az ismétlődő jegyek az 1/7,2/7,...,6/7 törtekben. Ezeken kívül más ilyen számok is vannak.
|
| Előzmény: [2272] jonas, 2007-09-17 12:37:15 |
|
|
|
| [2276] jonas | 2007-09-17 13:26:26 |
 Meglepő módon, noha hatjegyű példából (a) 7 (b) 2 is van, nemhogy ennél kisebb nincs, de hét- és nyolcjegyű szám sincs, ami teljesíti a feltételek valamelyikét.
|
| Előzmény: [2273] jonas, 2007-09-17 13:00:51 |
|
|
| [2278] diakmatekos | 2007-09-17 13:55:04 |
 Sziasztok! Itt egy érdekes, (talán inkább nehéz) feladat:
Legyen U vektortér az F test fölött, és jelölje End(U) összes lineáris transzformációi halmazát. Igazolnunk kellene, hogy End((U),+,*) gyűrű, ahol a két művelet a lineáris leképezések ismert összeadása és a leképezésszorzás.
a hozzákezdéshez kellene vmi ötlet. Remélem tudtok segíteni. köszi
|
|
|
| [2280] jonas | 2007-09-17 14:34:10 |
 Sőt, könnyen lehet, hogy sok másik példa is így áll elő, például 153846 az 1/13 jegyeiből; 102564 (a legkisebb ilyen szám) az 1/45-ből. Valójában az 1/7, 1/13, és 1/45 együtt magyarázatot adnak minden hatjegyű példa eredetére.
Érdekes feladat ez.
|
| Előzmény: [2275] Sirpi, 2007-09-17 13:07:29 |
|
| [2281] jonas | 2007-09-17 15:16:49 |
 Tizenegyjegyű sincs. Lehet, hogy majd lefuttatom a kimerítő keresést a tizenkétjegyűekre is, mert az egy napon belül biztosan végezne. Eddig tizenkétjegyűekből csak a hatjegyűek ismétlését ismerem, tizenháromjegyűből pedig a következőket: 1012658227848 és 1139240506329 (az 1/79 jegyei), valamint 102564102564.
|
| Előzmény: [2279] jonas, 2007-09-17 13:57:56 |
|
|
| [2283] Lóczi Lajos | 2007-09-17 15:48:45 |
 Csak írd fel részletesen, mely azonosságoknak kell egy gyűrűben teljesülniük (modellként vedd a számokat az összeadással és a szorzással, csak a szorzás ne legyen kommutatív) -- és mindegyik automatikusan teljesülni fog, mert a leképezések között az összeadás és a kompozíció úgy van definiálva, hogy ezek pont teljesüljenek...
|
| Előzmény: [2278] diakmatekos, 2007-09-17 13:55:04 |
|
|
| [2285] jonas | 2007-09-17 16:31:36 |
 Hát, engem például meglep, hogy a 17 nem szerepel, holott az 1/17 tizedes törtként 16 periódusú.
Természetesen az ilyen sorozatoknak a Sloane-ben érdemes utánanézni. Az (a) feladat megoldásait A034089 adja meg, de meglepő módon a (b) nincs benne.
|
| Előzmény: [2282] Lóczi Lajos, 2007-09-17 15:46:43 |
|
| [2286] jonas | 2007-09-17 22:34:43 |
 Ellenőriztem, valóban csak az a kilenc darab 12 jegyű megoldás van, amit a hétjegyűek ismétléseként kapunk. Elindítom a programot 13 jegyűre, elvileg két nap alatt végeznie kell.
|
|
| [2287] Sirpi | 2007-09-18 09:38:06 |
 Mielőtt leégne a nagy munkától a procid, próbáljuk meg "kicsit" szűkíteni a keresési teret.
Nézzük először a b) esetet, ott program nélkül is sikerült felderítenem az összes megoldást. Legyen a vizsgálandó n szám m+1-jegyű (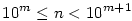 ), és írjuk fel n=10a+b alakban, ahol 1 ), és írjuk fel n=10a+b alakban, ahol 1 b b 9, és 10m-1 9, és 10m-1 a<10m, tehát az első m jegyből alkotott számot jelöli a, az utolsót pedig b. Vigyük b-t előre (az így kapott szám 10mb+a), és tegyük fel, hogy ettől a szám k-adrészére változik (mivel mindkét szám m+1 jegyű, és valódi osztót keresünk, ezért 2 a<10m, tehát az első m jegyből alkotott számot jelöli a, az utolsót pedig b. Vigyük b-t előre (az így kapott szám 10mb+a), és tegyük fel, hogy ettől a szám k-adrészére változik (mivel mindkét szám m+1 jegyű, és valódi osztót keresünk, ezért 2 k k 9): 9):
10a+b=k(10mb+a)
Innen
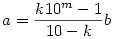
Az első észrevétel, hogy ha k>5, akkor a jobb oldal több, mint m-jegyű, hiszen legalább 5.10m-t osztjuk legfeljebb 4-gyel, amit még b-vel meg is szorzunk, ez már b=1 esetén is nagy.
Ha k=5, akkor a=499...9/5.b, viszont ekkor b csak 5 lehet, hogy egész számot kapjunk, megint nagy lesz a (499...9).
k=4 esetén a=399...9/6.b, itt b-t legalább 2-nek kell választanunk, hogy egész számot kapjunk, de b=2 esetén a=133...3, ami szintén sok. A k=3 esetet a végére hagyom, mert az az érdekes. k=2-re a=199...9/8.b, itt b csak 8 lehet, ekkor a=199...9, szintén túlcsordul.
Ha k=3, akkor a=299...9/7.b, ha b=7 lenne, akkor túl nagy számot kapnánk, ezért a 299...9 számnak oszthatónak kell lennie 7-tel. A 10m 7-es maradékai rendre (0-tól kezdve) 1, 3, 2, 6, 4, 5, és innentől ismétlődik, ezt 3-mal szorozva, majd 1-et kivonva a 2, 1, 5, 3, 4, 0 periódusú sorozatot kapjuk.
Az jött ki tehát, hogy csak akkor van megoldás, ha m+1 osztható 6-tal, és ilyenkor hogy elkerüljük a túlcsordulást, b csak 1 vagy 2 lehet.
Ekkor a következő megoldások adódnak:
428571 142857 (b=1) 142857 (b=1)
857142 285714 (b=2) 285714 (b=2)
428571428571 142857142857 (b=1) 142857142857 (b=1)
857142857142 285714285714 (b=2) 285714285714 (b=2)
stb.
Tehát a két alapmegoldás (amit a 3/7 és a 6/7 tizedestört alapjából kapunk) néhányszor egymás mögé írásával adódik az összes megoldás.
|
| Előzmény: [2286] jonas, 2007-09-17 22:34:43 |
|
| [2288] Sirpi | 2007-09-18 10:00:38 |
 Ugyanúgy intézhető el az a) eset, ekkor
k(10a+b)=10mb+a
ahonnan
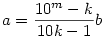
Rögzített m-re tehát elég végignézni a b=1,2,...,9, k=2,3,...,9 eseteket, ami összesen 72 db. ellenőrzést jelent (ez pl. m+1=13-ra, amit épp vizsgálsz, Jónás, elég messze van a 2 naptól, még akár kézzel is ;-) ).
Nyilván lehet további egyszerűsítéseket tenni, pl. k=3-ra a 10m-3-nak oszthatónak kell lennie 29-cel, ami csak akkor teljesülhet, ha m+1 osztható 28-cal (és ilyenkor b=3,4,5,6,7,8,9 mind megoldást ad, b=1,2 még túl kicsi).
És az is látszik ebből a felírásból, hogy miért jöttek ki ezek a furának ható törtek, pl. az 1/13. Ha k=4, akkor a=99...96/39.b=33...32/13.b, és már meg is jelent a 13-as nevező (és a számlálóból a -k-t elhanyagolva kapjuk, hogy 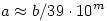 ). ).
Egyébként m=5-re (vagyis a 6-jegyű n-ekre) a következő megoldások adódtak:
230769 923076 (k=4,b=9) 923076 (k=4,b=9)
205128 820512 (k=4,b=8) 820512 (k=4,b=8)
179487 717948 (k=4,b=7) 717948 (k=4,b=7)
153846 615384 (k=4,b=6) 615384 (k=4,b=6)
128205 512820 (k=4,b=5) 512820 (k=4,b=5)
102564 410256 (k=4,b=4) 410256 (k=4,b=4)
142857 714285 (k=5,b=7) 714285 (k=5,b=7)
Más k-ra nem adódik megoldás. Innentől lehet progit írni, hogy a többi m-re is végignézzük a lehetőségeket, de szerintem az is járható út, hogy végignézzük a k=2,3,...,9 eseteket, és mindegyikre megnézzük, hogy mely m-ekre ad megoldást. Nagyon úgy néz ki, hogy ha két megoldást azonosnak tekintünk akkor, ha ugyanannak a blokknak a többször egymás után írásával adódnak, akkor csak véges sok megoldás van összesen.
|
| Előzmény: [2287] Sirpi, 2007-09-18 09:38:06 |
|
|
| [2290] Yegreg | 2007-09-18 17:18:57 |
 Legyen a,b,c egy háromszög oldalainak hossza. Vegyük az a/b, b/a, b/c, c/b, c/a, a/c számok közül az 1-nél nem kisebbeket, és legyen ezek közül x a legkisebb. Milyen nagy lehet x?
|
|
| [2291] Sirpi | 2007-09-18 17:27:20 |
 Köszi. Mindezt csak Jónás gépének védelmében tettem :-)
Egyébként még annyi kiegészítés az a) részhez, hogy tovább lehet csökkenteni a vizsgálatok számát, ugyanis
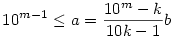
Innen azt kapjuk, hogy 10b>10k-1-nek teljesülnie kell, vagyis b k. így elég 36 esetet megnézni. k. így elég 36 esetet megnézni.
Tehát ha pl. k=9, akkor b=9, vagyis a=9.(10m-9)/89, és a legkisebb m, amire ez egész, az m=43, ahonnan rögtön kapunk egy elvileg nem periodikus 44 jegyű megoldást. Hasonlóan k=8-ra m=12.
k=7-re a nevező 69, vagyis 3.23. m=21-re a számláló osztható 69-cel (nincs kisebb, ami osztható lenne 23-mal), ebből is kapunk egy megoldást.
Hasonlóan végig lehetne nézni az összes k-t, csak nekem ehhez nincs sok türelmem :-)
* * *
Azért pár példa, amit kiszámoltam:
91011235955056179775280898876404494382022471 / 10112359550561797752808988764044943820224719 = 9
8101265822784 / 1012658227848 = 8 (ez pont 13 jegyű :-) )
210526315789473684 / 105263157894736842 = 2
2 és 9 között minden arányra van megoldás.
|
| Előzmény: [2289] Lóczi Lajos, 2007-09-18 12:40:43 |
|
| [2292] SmallPotato | 2007-09-18 19:13:33 |
 Legyen mondjuk a b b c. Ekkor a három, érdemben vizsgálandó, egynél nem kisebb hányados c. Ekkor a három, érdemben vizsgálandó, egynél nem kisebb hányados 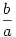 , , 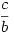 és és 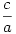 . Ezek közül (a kiinduló reláció értelmében) . Ezek közül (a kiinduló reláció értelmében) 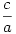 nem lehet a legkisebb; marad tehát nem lehet a legkisebb; marad tehát 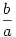 (legyen ez p; ekkor b=ap) és (legyen ez p; ekkor b=ap) és 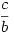 (legyen ez q; ekkor c=bq). Értelemszerűen p (legyen ez q; ekkor c=bq). Értelemszerűen p 1 és q 1 és q 1. 1.
A háromszög oldalaira vonatkozó egyenlőtlenség értelmében c<a+b. Ebbe helyettesítsük be b=ap és c=bq=apq értékét; kapjuk
apq<a+ap
Innen a-val osztva (mivel a>0, az osztás elvégezhető és az egyenlőtlenség iránya is változatlan):
pq<1+p
Innen p-vel osztva (p>0 miatt az osztás elvégezhető és az egyenlőtlenség iránya is változatlan):
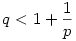
Tekintve, hogy p 1, kapjuk, hogy q<2. Ha azonban q "2-höz közeli" érték, akkor láthatóan p-nek "1-hez közelinek" kell lennie, tehát ilyenkor p a kisebb. p növelésével egy ponton p és q egyenlővé válik; ez a pont (az egyenlőtlenséget egyenlőségként megoldva pl p-re) 1, kapjuk, hogy q<2. Ha azonban q "2-höz közeli" érték, akkor láthatóan p-nek "1-hez közelinek" kell lennie, tehát ilyenkor p a kisebb. p növelésével egy ponton p és q egyenlővé válik; ez a pont (az egyenlőtlenséget egyenlőségként megoldva pl p-re)
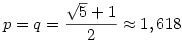
. Ha p ennél nagyobb, akkor q (ennél és így p-nél is) kisebb.
p és q közül a kisebbik tehát az 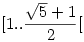 jobbról nyílt intervallumba kell hogy essen. (ha "nem nagyobbik" lett volna a kérdés, akkor az intervallum jobbról is zárt lenne.) jobbról nyílt intervallumba kell hogy essen. (ha "nem nagyobbik" lett volna a kérdés, akkor az intervallum jobbról is zárt lenne.)
|
| Előzmény: [2290] Yegreg, 2007-09-18 17:18:57 |
|
| [2293] SmallPotato | 2007-09-18 19:27:16 |
 Tulképpen nem véletlen, hogy az aranymetszés aránya jön ki: tegyük fel, hogy a háromszög c=a+b jelleggel elfajul; ekkor ha a c oldalt a C csúcs az aranymetszés szerint osztja, akkor per definitionem 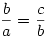 ; ellenkező esetben valamelyik arány a ; ellenkező esetben valamelyik arány a 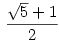 -nél kisebb, a másik pedig nagyobb. -nél kisebb, a másik pedig nagyobb.
(Ez a "levezetés" természetesen nem tartalmazza a nem-elfajult esetet.)
|
| Előzmény: [2292] SmallPotato, 2007-09-18 19:13:33 |
|
| [2294] Yegreg | 2007-09-18 19:29:55 |
 Igen, szép megoldás, nekem is ez adódott. A kérdés egyébként úgy is lefordítható, hogy "mennyire lehet nem egyenlőszárú egy háromszög?", ebből már sejthető, hogy miért is vetődött fel bennem a feladat. :)
|
|
| [2295] SmallPotato | 2007-09-18 19:42:39 |
 Csak nem "általános háromszög"et akartál felskiccelni? :-))
(Esetemben a lehetséges kimenetelek: egyenlőszárú, derékszögű, ... és hovatovább a
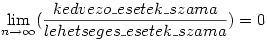
tárgyában merül fel a kérdés :-D)
|
| Előzmény: [2294] Yegreg, 2007-09-18 19:29:55 |
|
| [2296] Sirpi | 2007-09-18 19:59:47 |
 Na, megvan az összes megoldás, a gép pihenhet (és végre Nektek se kell tovább olvasgatnotok a fejtegetéseimet :-) )
Szóval odáig jutottam, hogy 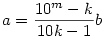 , és 2 , és 2 k k b b 9 9
Tegyük fel, hogy adott k-ra van megfelelő b és m. Ekkor
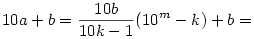
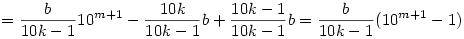
Ha a 10k-1 prím, akkor olyan m kell, amire 10m k(mod10k-1), de ekkor 10m+1 k(mod10k-1), de ekkor 10m+1 10k 10k 1(mod10k-1). Vagyis ha m+1-esével növelem a kitevőt, akkor mindig új megoldásokat kapok, és azt is könnyű látni, hogy ezek mind az alapmegoldás egymás után írásai lesznek, hiszen 1(mod10k-1). Vagyis ha m+1-esével növelem a kitevőt, akkor mindig új megoldásokat kapok, és azt is könnyű látni, hogy ezek mind az alapmegoldás egymás után írásai lesznek, hiszen
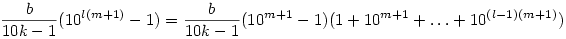
és itt az utolsó tényezó kivételével épp az alapmegoldás van felírva, az utolsó tényező pedig 100...0100...01...100...01 alakú, így a vele való szorzás épp az egymás után írást eredményezi,
Ezzel tehát elintéztük a k=9 (10k-1=89), k=8 (79), k=6 (59), k=3 (29), és k=2 (19) eseteket.
Konkrétan a megoldások (a kitevők onnan jönnek, hogy megkerestem a 10m k legkisebb megoldását) (l=1,2,...): k legkisebb megoldását) (l=1,2,...):
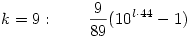
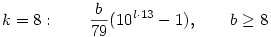
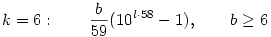
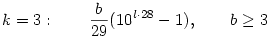
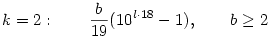
Marad még a k=7 (69), 5 (49) és 4 (39). A 7 és a 4 egyszerűbb, ugyanis ott az első olyan m index, ahol 10m-k osztható 23-mal illetve 13-mal, egyúttal osztható 69-cel, illetve 39-cel is, tehát ezek a megoldások ugyanolyanok, mint amit a prímeknél kaptunk:
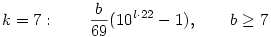
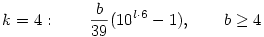
A legérdekesebb a k=5 eset, ugyanis ott 49 a nevező, ezért előfordulhat, hogy a 10m-5 is osztható 7-tel, és b=7. Ezek a köv. megoldások:
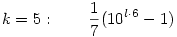
És van az az eset, mikor 10m-5 osztható 49-cel, ebből a következő megoldások adódnak:
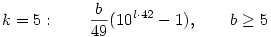
Ez lenne tehát az összes megoldás, és igérem, leszálltam a feladatról.
|
| Előzmény: [2291] Sirpi, 2007-09-18 17:27:20 |
|
| [2297] jonas | 2007-09-18 22:21:41 |
 Érdekes.
Nekem most már csak azt kell ellenőriznem, hogy a heurisztikusan közelítő programom, ami a [2279] hozzászólás tizenháromjegyű megoldásait találta, minden megoldást megtalált-e (eltekintve az ismétlésektől).
Ez a program úgy működött, hogy az x=a(10m-1)/b kifejezésbe helyettesített be olyan kis számokat, ahol m osztja b-1-et, majd ellenőrizte a kapott x-et.
Elég sok megoldást megadott, a legtöbbet sokféle paraméterekkel újra meg újra.
|
| Előzmény: [2296] Sirpi, 2007-09-18 19:59:47 |
|
| [2298] jonas | 2007-09-18 22:23:50 |
 Egyébként nem az otthoni gépemen fut, noha az is elég jó gép, de az egyetem kétszer két magos AMD procis gépe gyorsabb.
|
|
| [2299] jonas | 2007-09-18 23:01:11 |
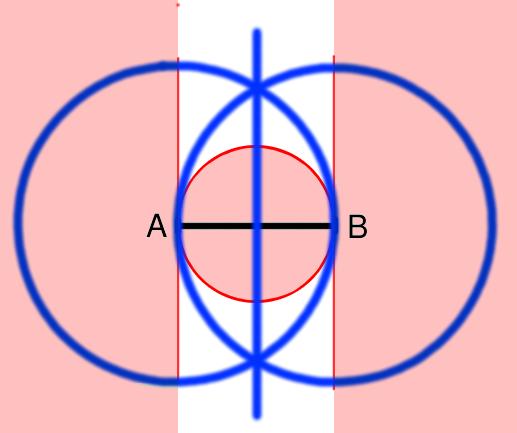
 Igen, ismert tétel, hogy általános háromszöget nehéz rajzolni. Reiman tanár úr ezt a következő módon bizonyította.
Rögzíthetjük a háromszög két csúcsát, mivel hasonlóság erejéig nem változtat a feladaton. Nézzük meg, hova rakhatjuk a harmadik pontot. A piros területek ki vannak zárva, mivel akkor tompaszögű lenne a háromszög. Ki van zárva az őket határoló piros vonalak környéke is, hiszen akkor majdnem derékszögű lenne a háromszög. A kék vonalak környéke pedig azért van kizárva, mert akkor majdnem egyenlőszárú lenne a háromszög. Nagyon magasra sem érdemes rakni a csúcsot, mert akkor csúnyán megnyúlt háromszöget kapunk, amit ráadásul könnyebben lehet egyenlőszárúnak nézni, mivel két oldala közel azonos hosszú.
Az pedig látható, hogy így nem marad sok hely, ahova a harmadik pontot le lehetne tenni.
|
 |
| Előzmény: [2295] SmallPotato, 2007-09-18 19:42:39 |
|
| [2300] SmallPotato | 2007-09-19 07:19:19 |
 Örömmel látom, hogy esetenkénti bénázásom mily mély matematikai alapokon nyugszik. :-)
Soha nem jutott eszembe, hogy vizsgáljam az okokat ... de az ábra és a kommentár valóban meggyőző!
|
| Előzmény: [2299] jonas, 2007-09-18 23:01:11 |
|
| [2301] BohnerGéza | 2007-09-19 09:35:31 |
 Szerintem a fehér pontok esetén sem általános, hanem hegyesszögű háromszöget kapunk! Vége! Talán az AB-n van C, akkor nem hegyes-, nem derék- és nem tompaszögű az ABC.
|
| Előzmény: [2299] jonas, 2007-09-18 23:01:11 |
|
|
|
|
| [2305] rizsesz | 2007-09-19 22:49:04 |
 Sziasztok. Meg tudnátok mondani az a2=1, a3=2 an+1=(an+an-1)*(n-1) rekurzió megoldását mondani?
|
|
|
| [2307] rizsesz | 2007-09-20 08:06:28 |
 Fontosak az alsó indexek. Itt a4=9.
|
|
|
|
| [2310] rizsesz | 2007-09-20 08:50:54 |
 Te ezt írtad: a4=(a2+a3)(3-1)=(1+2)*2=6. Én ezt: a4=(a2+a3)(4-1)=(1+2)*3=9. Az indexálással tolódik az n-1-es szorzó is.
|
|
|
|
|
| [2314] nadorp | 2007-09-20 11:26:51 |
 Tehat, a1=0,a2=1 és an+1=n(an+an-1) ( Ekkor persze a3=2, mint az eredeti kiírásban).
Legyen 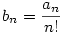 . Ekkor b1=0, . Ekkor b1=0, 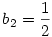 . .
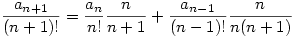 , azaz , azaz
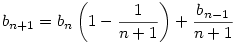
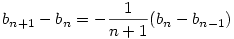 . Innen indukcióval . Innen indukcióval
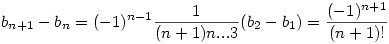 . .
Ha most a fenti összefüggést elvégezzük k=2,3,...(n+1) értékekre és összeadjuk ezeket, akkor
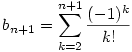 , azaz , azaz
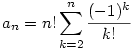
|
| Előzmény: [2312] rizsesz, 2007-09-20 09:14:10 |
|
| [2315] rizsesz | 2007-09-20 12:54:28 |
 Köszönöm mindkettőtöknek, tetszenek. Egyébként ez a rekurzió a következő feladatnál került elő: Hányféleképpen lehet sorba rakni az 1, 2, ... n számokat, hogy semelyik se a saját értékének megfelelő helyen szerepeljen? Erre jött ki, hogy n= 2, 3, 4, 5 értékére 1, 2, 9, 44 a sorbarendezések száma, és ez összhangban van a rekurzióval (csak még ki kéne találni a származtathatóságot). Egyébként kedves nadorp, a talált képlet nem Taylor-sora semminek?
|
| Előzmény: [2314] nadorp, 2007-09-20 11:26:51 |
|
|
|
| [2318] Sirpi | 2007-09-20 13:10:39 |
 Mármint n=0-tól megy az indexelés, nem? Viszont jelen esetben tényleg igaz, hogy an n!/e, hiszen a 0. és első tag összege: (-1)0/0!+(-1)1/1!=1-1=0, tehát tényleg elég a 2. tagtól összegezni. n!/e, hiszen a 0. és első tag összege: (-1)0/0!+(-1)1/1!=1-1=0, tehát tényleg elég a 2. tagtól összegezni.
|
| Előzmény: [2316] nadorp, 2007-09-20 13:07:02 |
|
|
| [2320] rizsesz | 2007-09-20 14:23:48 |
 és akkor egyúttal a szitaformulával is ez jön ki?
|
|
|
| [2322] rizsesz | 2007-09-20 15:39:46 |
 Tökéletes. :) Igazából az volt a feladat, hogy n gyerek karácsonyi ajándék-húzásba kezd, és az első n-1 embernek lehetősége van arra, hogy újra húzzon, ha önmagát húzta. A kérdés annak az volt, hogy mi annak a valószínűsége, hogy az n. ember önmagát húzza. Ezt én úgy definiáltam, hogy a jó esetek száma az, hogy az első n-1 ember nem húzza önmagát, azaz az előző értelmezésekben an-1, míg az összes eset an, így a megoldás ezek hányadosa.
|
| Előzmény: [2321] Lóczi Lajos, 2007-09-20 14:34:13 |
|
|
| [2324] rizsesz | 2007-09-21 08:38:13 |
 A jó esetek azt jelentik, hogy az n. húzza ki magát az n. esetben, tehát az első n-1-et kell vizsgálni, akikre igaz, hogy egymás között senki nem húzta ki magát. Ez pedig szerintem tökéletesen reprezentálható an-1-gyel.
|
|
| [2325] Gyöngyő | 2007-09-24 22:42:32 |
 Sziasztok! Tudnátok segíteni a következő feladatban: Egy összefüggést kell megsejteni: 93+123+153=183 283+533+753=843 653+1273+2483=2603
Köszönettel: Zsolt
|
|
|
| [2327] Gyöngyő | 2007-09-25 12:25:16 |
 Köszike Nadorp!
este én is rájöttem a megoldásra,és ráadásul nem is ezt a feladatot akartam elküldeni,szerintem ennek a feladattípusnak van egy nehezebb változata.Én nem jövök rá sehogysem: 33+43+53=63 és 123+193+533=543 273+463+1973=1983 ra. Az első tagokat sikerült beazonosítanom,de a többivel van a gondom! Előre is köszönöm!
Üdv: Zsolt
|
| Előzmény: [2326] nadorp, 2007-09-25 10:24:20 |
|
|
| [2329] Lbandi | 2007-09-26 21:59:47 |
 Sziasztok! Már egy pár órája a következő feladattal bajlódok: a*x+b*y=c, lineáris diofantoszi egyenletnek létezik megoldása, azaz lnko(a,b) osztja c-t. Mennyi lehet lnko(x,y)?
Nyilván lnko(x,y) osztja c-t, de azt nem sikerült még bizonyítanom, hogy c minden osztójára létezik x,y úgy hogy lnko(x,y)=c, vagy hogy c-nek csak bizonyos osztóira (például csak c/(lnko(a,b)) osztóinak mindegyikére). Persze az is lehet, hogy nem vettem észre valami triviálisat, mindenesetre előre is köszönök minden hozzászólást :)
|
|
| [2330] Hajba Károly | 2007-09-27 01:19:51 |
 Ha a*x+b*y=c egyenletnek van megoldása, akkor végtelen megoldása van, mivel a*(x-n*b)+b*(y+n*a)=c is igaz. n tetszőleges egész.
S mivel két relatív prím valahányszori összeadásával a két szám szorzatánál nagyobb bármely szám előállítható, így ha a és b relatív prímek c tetszőleges lehet, lesz az egyenletnek megoldása, s végtelen számú.
|
| Előzmény: [2329] Lbandi, 2007-09-26 21:59:47 |
|
| [2331] Lbandi | 2007-09-27 08:56:05 |
 Köszönöm a hozzászólást, de attól tartok nem lettem tőle okosabb. Azt eddig is tudtam, hogy egy ilyen egyenletnek vagy nincs megoldása, vagy végtelen sok van. A kérdés az, hogy adott a, b és c paraméterekkel mennyi lehet x és y legnagyobb közös osztója (feltételezve, hogy megoldható persze). Nyilván nem lehet akármi, hiszen legalább a c-t osztania kell a közös osztónak, de ez még nem egy kimerítő megoldás. Bocs, ha nem volt elég tiszta a feladat megfogalmazása, vagy ha valamit félreértettem a hozzászólásodban.
|
| Előzmény: [2330] Hajba Károly, 2007-09-27 01:19:51 |
|
| [2332] Yegreg | 2007-09-27 13:11:15 |
 Egyrészt, ax+by többszöröse (a,b)(x,y)-nak, tehát (a,b)(x,y)|c, azaz 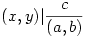 . Legyen . Legyen 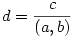 . Belátjuk, hogy d|(x,y) is lehetséges, ez ekvivalens azzal, hogy létezzen k, l egész, hogy x=kd, y=ld. Ekkor az egyenletünk akd+bld=c alakú. Legyen . Belátjuk, hogy d|(x,y) is lehetséges, ez ekvivalens azzal, hogy létezzen k, l egész, hogy x=kd, y=ld. Ekkor az egyenletünk akd+bld=c alakú. Legyen 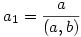 , , 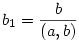 (látszik, hogy (a1,b1)=1), illetve legyen (látszik, hogy (a1,b1)=1), illetve legyen 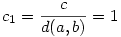 ! Az egyenletünk (a,b)d-vel való leozstás után az a1k+b1l=c1 alakot ölti, ahol a1,b1,c1 egész, tehát ez egy lineáris diofantoszi egyenlet k,l-re, továbbá (a1,b1)=1|c1, tehát az egyenletnek van is megoldása. ! Az egyenletünk (a,b)d-vel való leozstás után az a1k+b1l=c1 alakot ölti, ahol a1,b1,c1 egész, tehát ez egy lineáris diofantoszi egyenlet k,l-re, továbbá (a1,b1)=1|c1, tehát az egyenletnek van is megoldása.
Azt kaptuk tehát, hogy (x,y)|d, de van olyan x és y, hogy d|(x,y), tehát ezekre (x,y)=d.
|
|
| [2333] Hajba Károly | 2007-09-28 00:42:05 |
 Valóban. Tegnap már nagyon késő volt és egy mondat még lemaradt. A több megoldás közül melyikre keresed az lnko-t, mert szerintem a, b, c paraméteres ismeretében ez nem egyszerű feladat.
De nézzünk egy kokrét példát:
3x+5y=61
x:y = 2:11; 7:8; 12:5 és 17:2 ha a pozitív eredményeket tekintjük. Tehát elég bonyolult függvény adhatja meg paraméteresen lnko(x,y) lehetséges értékeit.
Kicsit továbbgondoltam a feladatot, pontosabban azt, hogy mikor megoldható az alapegyenlet. Úgy tűnik, két esetben nincs megoldhatóság:
Ha (a=b)&(c 2*n*a) ill. ha páros(a,b)&páratlan(c) 2*n*a) ill. ha páros(a,b)&páratlan(c)
|
| Előzmény: [2331] Lbandi, 2007-09-27 08:56:05 |
|
| [2334] Lbandi | 2007-09-28 20:49:15 |
 Köszönöm a válaszokat, tényleg elég nehéznek tűnik paraméteresen megadni a megoldást, egy kicsit hanyagul megfogalmazott a feladat evvel a "mi lehet lnko(x,y)?"-nal.
|
|
| [2335] epsilon | 2007-09-30 11:18:35 |
 Tisztelt Kollégák! Egy érdekes egyenlőtlenseég vezetett a következő kérdéshez: ha fennáll a következő egyenlőtlenséglánc, akkor igaz-e az egészrészre vonatkozó eredmény? Ha n négyzetszám, akkor Nekem kijött, de általában?Előre is köszönöm a válaszotokat!
|
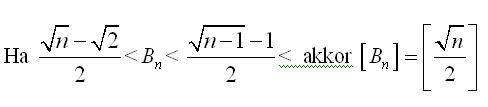 |
|
|
| [2337] epsilon | 2007-09-30 14:31:32 |
 Bocs, az egészrész nem az, és az egyenlőtlenségeket is megnézem, ha valamit elszámoltam volna.Továbbá n>2. Az egészrészes ez kell legye:
|
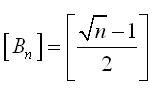 |
|
|
| [2339] epsilon | 2007-09-30 15:26:31 |
 Igen, valóban erre sem jó, Én kicsi teljes négyzetekre, majd n=100 értékére próbáltam, ezekből próbáltam arra következtetni amit írtam, de hibásan :-( Végül is az érdekelne, hogy egyenlőek-e az An és Bn egészrészei, és mivel is egyenlőek ezek, ha n>=2 pozitív egész, és:
|
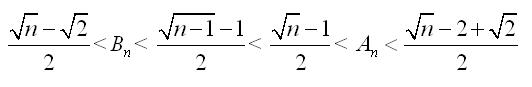 |
|
| [2340] epsilon | 2007-09-30 16:03:04 |
 Ha nem tévedtem, akkor az egészrészes eredmény páros teljes négyzet esetén mégis igaz, vagyis:
|
 |
|
| [2341] epsilon | 2007-09-30 16:27:08 |
 Bocs, hogy így szotyogtatom, ez még kijött, és az a sejtésem, hogy a 2 eset eredményeit kapjuk más n számok esetén is de, hogy mikor melyiket, még nem látom :-(
|
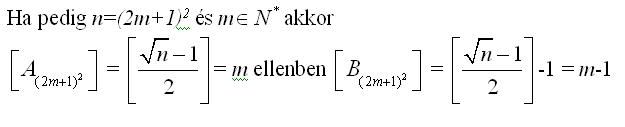 |
|
|
|
| [2344] nadorp | 2007-09-30 20:05:12 |
 határozzik meg sin 3o pontos értékét középiskolai módszerekkel
|
|
|
|
| [2347] Lóczi Lajos | 2007-09-30 23:13:51 |
 [Nyilván 3=18-15, és a félszögképlet miatt csak a 18 fok szinuszán kell kicsit gondolkodni, de a példatárakban (pl. Geom. feladatgyűjtemény) az aranymetszésnél ez utóbbi szög szinusza is ki van számolva (Mathematica alatt: Sin[3 Degree] // FunctionExpand, weben (még egy felezésre szükség van): http://functions.wolfram.com/ElementaryFunctions/Sin/03/02/).]
|
| Előzmény: [2344] nadorp, 2007-09-30 20:05:12 |
|
|
| [2349] SmallPotato | 2007-09-30 23:48:36 |
 A 18 fokos szög szögfüggvényeinek megállapításához (a készen kapható ötleteken kívül, persze) a 72-72-36 fokos szögekkel bíró egyenlőszárú háromszöget javaslom; ennek oldalarányai (ha ugyan fejből nem ismertek :-) ) annak felismerésével határozhatók meg, hogy az egyik 72 fokos szög felezője a szemközti oldalból saját magával azonos hosszúságú szakaszt metsz ki, a másik metszék pedig egy újonnan keletkezett kisebb, szintén 72-72-36 fokos háromszög legkisebb oldala.
|
| Előzmény: [2348] SmallPotato, 2007-09-30 23:40:47 |
|
|
| [2351] nadorp | 2007-10-01 09:45:33 |
 Köszönöm a hozzászólásokat. Én Lóczi Lajoshoz hasonlóan csináltam. A sin(x+15o)=sin18o egyenletnek a 3o és 147o a megoldása. Ez a sin xcos15o+cos xsin15o=sin18o egyenletre vezet. Ebből sin x-re egy másodfokú egyenletet kapunk, aminek a kisebbik gyöke sin3o
|
|
|
| [2353] SmallPotato | 2007-10-02 14:29:53 |
 "Egy kocka 3 kitérő élétől egyenlő távolságra levő pontok halmaza micsoda?"
Erős meggyőződésem szerint a kérdéses mértani hely egy egyenes. Konkrétan az az egyenes, amely tartalmazza a kockának azon (egyetlen) testátlóját, amely mindhárom jelzett kitérő élhez képest kitérő.
Bizonyítani sajnos nem tudom. :-(
Eljutottam egy ilyen, a kérdéses mértani hely (x,y,z) pontjait leíró egyenletrendszerhez (a kocka élhossza 2a, élei a koordinátatengelyekkel párhuzamosak, középpontja az origóban):
(a-y)2+(a+z)2 = (a-z)2+(a+x)2 = (a-x)2+(a+y)2
Ennek a jelzett egyenes pontjai valóban eleget tesznek - de elvben talán más pontok is? Nem tudom.
|
| Előzmény: [2255] rizsesz, 2007-09-02 20:52:05 |
|
| [2354] rizsesz | 2007-10-02 15:18:11 |
 Ezekből az egyenletekből páronként 2x=y+z, 2y=x+z, 2z=x+y, és ezekből x=y=z könnyen jön, ami valóban az említett egyenes. nem :D?
|
|
|
| [2357] epsilon | 2007-10-06 08:57:35 |
 Helló! A következő kérdésre nem találok azonnali választ :-( "Ihazoljuk, hogy minden nemnegatív n egész szám esetén 8n+10 felírható két páratlan egész szám négyzetösszegeként!" Bármilyen tippet előre is köszönök! Üdv: epsilon
|
|
|
| [2359] epsilon | 2007-10-06 13:40:30 |
 Köszi, egy átalakításnál elnéztem a feladatot ami erre vezetett. Valójában az érdekelne, hogy milyen a, b, c, pozitív egész számok esetén van nemnegatív egészekből álló megoldása az alábbi egyenletnek, minden n pozitív egész számra. Szakirodalom a neten, az is érdekelne! Előre is kösz!
|
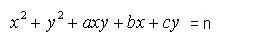 |
| Előzmény: [2357] epsilon, 2007-10-06 08:57:35 |
|
| [2360] Róbert Gida | 2007-10-06 16:47:17 |
 x=0,y=0 esetén p(x,y)=0
x>0 vagy y>0-ra p(x,y)>1 Azaz már az 1 sem áll elő. A helyzet még ennél is rosszabb, ugyanis végtelen sok pozitív egész szám nem áll elő, ezt a megoldások számának triviális felső becslésável lehet belátni, n=K2-ig tekintve a megoldásokat.
|
| Előzmény: [2359] epsilon, 2007-10-06 13:40:30 |
|
| [2361] nadorp | 2007-10-06 18:19:25 |
 Ha x2+y2=8n+10, akkor x és y azonos paritású, tehát, 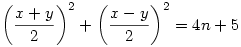 miatt 4n+5 is két egész szám négyzetösszege. Ismert, hogy egy egész szám akkor lehet két egész négyzetösszege, ha a prímtényezős felbontásában minden 4k-1 alakú prím páros kitevőn szerepel. Ebből következik, hogy például a miatt 4n+5 is két egész szám négyzetösszege. Ismert, hogy egy egész szám akkor lehet két egész négyzetösszege, ha a prímtényezős felbontásában minden 4k-1 alakú prím páros kitevőn szerepel. Ebből következik, hogy például a
3.7(2x-1)2=21(2x-1)2
alakú számok nem állnak elő két egész négyzetösszegeként, tehát a 42(2x-1)2 alakúak sem, pedg 8n+10 alakúak
|
| Előzmény: [2357] epsilon, 2007-10-06 08:57:35 |
|
|
|
|
|
| [2366] epsilon | 2007-10-07 10:07:22 |
 Elfelejtettem pontosítani: x és y nemnegatív egészek lehetnek!
|
|
| [2367] Róbert Gida | 2007-10-07 13:14:52 |
 Most szórakozol, vagy mi? Egyetlen szóval sem írtad, hogy páros nemnegatív számokra kérted csak az előállítást. Egyébként, ahogy megoldottam úgy is teljesen értelmes feladat volt. Gondolatolvasó pedig (még) nem vagyok.
Itt az új feladat megoldása, bár lövésem sincs, hogy most ezt akarod-e megoldani: x2+y2+2*x*y+x+3*y=2*n-nek keressük nemnegatív egész megoldását minden n 0-ra. x-re rendezve az egyenletet: 0-ra. x-re rendezve az egyenletet:
x2+(2*y+1)*x+(y2+3*y-2*n)=0
Ennek a megoldásai:
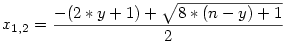
Legyen a az az egyértelműen meghatározott nemnegatív egész szám, amelyre teljesül, hogy (2*a+1)2 8*n+1<(2*a+3)2. Ekkor, mivel minden páratlan négyzetszám 8k+1 alakú, ezért van olyan nemnegatív y, amelyre: 8*(n-y)+1=(2*a+1)2, innen 8*n+1<(2*a+3)2. Ekkor, mivel minden páratlan négyzetszám 8k+1 alakú, ezért van olyan nemnegatív y, amelyre: 8*(n-y)+1=(2*a+1)2, innen 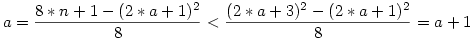 azaz y azaz y a, ezért a, ezért  és persze egész, ami kellett, így valóban minden nemnegatív páros egész előáll nemnegatív x,y segítségével, a bizonyításból egyébként az is kiderül,némi munkával, hogy az előállítás ráadásul egyértelmű. és persze egész, ami kellett, így valóban minden nemnegatív páros egész előáll nemnegatív x,y segítségével, a bizonyításból egyébként az is kiderül,némi munkával, hogy az előállítás ráadásul egyértelmű.
|
| Előzmény: [2365] epsilon, 2007-10-07 09:37:55 |
|
|
| [2369] epsilon | 2007-10-07 13:31:32 |
 Kedves Róbert Gida! Valóban szórakozom, de nem mással, mint éppen ez utóbbi feladatnak egy másik megoldásával és az általánosításával. Ha észrevetted, a 2359-es hozzászólás ezt a feladatot általánosítja, éppen ezért, ott az n nem csak páros. Tehát, ha ez utóbbi annak a sajátos esete, akkor érthető, hogy sajátos számok, feltételek állnak ez esetben.
|
| Előzmény: [2367] Róbert Gida, 2007-10-07 13:14:52 |
|
| [2370] rizsesz | 2007-10-08 20:57:16 |
 (a-y)ad2+(a+z)ad2 = (a-z)ad2+(a+x)ad2 = (a-x)ad2+(a+y)ad2
Ha a szobában vizsgálódunk, akkor feltehető, hogy x, y és z is egyaránt kisebb, mint "a". Ekkor az f(x)=(a-x)ad2 fv. szig. mon. csökkenő, míg g(x)=(a+x)ad2 szig. mon. nő a>0, x>0 miatt. Ha tehát x>=y, akkor (a-z)ad2+(a+x)ad2 = (a-x)ad2+(a+y )ad2 miatt (a-z)ad2<=(a-x)ad2 innen z>=x.
(a-y)ad2+(a+z)ad2 = (a-z)ad2+(a+x)ad2 is igaz viszont, és ebből teljesen hasonlóan y>=z, ami az előzőek miatt azt jelenti, hogy y>=z>=x>=y, ami azt jelenti, hogy csak az lehetséges, hogy a 3 szám egyenlő.
(valamiért nem megy semmi a teX-kel kapcsolatban :(). Az ad a hatvány-jel.
|
| Előzmény: [2353] SmallPotato, 2007-10-02 14:29:53 |
|
|
| [2372] SmallPotato | 2007-10-08 21:44:00 |
 Értem, köszönöm!
(Az efféle "körszimmetrikus" egyenletrendszerekkel többnyire elakadok: érzem én, hogy ha pontosan egyformán fordulnak elő a változók, akkor egyenlőknek kell lenniük - csakhát az érzés nem bizonyítás, ugye ... :-)) )
|
| Előzmény: [2370] rizsesz, 2007-10-08 20:57:16 |
|
|
|
|
|
|
|
|
| [2380] Csimby | 2007-10-14 12:54:23 |
 329. feladat (Nyilván nem a 329.-edik, de ez volt az az utolsó sorszám amit találtam, 10 oldallal korábban és azt is én írtam... Szerintem nem olyan megerőltető odaírni hogy hanyadik feladatról van szó, viszont úgy sokkal egyszerűbb hivatkozi rá)
Az 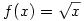 függvénygörbét forgassuk el az origó körül 45°-kal az óramutató járásával megegyező irányba. Mi az így kapott görbe egyenlete? függvénygörbét forgassuk el az origó körül 45°-kal az óramutató járásával megegyező irányba. Mi az így kapott görbe egyenlete?
|
|
| [2381] jonas | 2007-10-14 16:36:28 |
 (Szerintem egyébként a hozzászólás sorszáma alapján könnyebb hivatkozni. Adott sorszámú hozzászólást könnyebb megkeresni, mint adott sorszámú feladatot, különösen, ha nem nagyon sűrűn vannak feladatok a topikban. Ráadásul így nem fordulhat elő, hogy valaki tévedésből rossz sorszámot ad, vagy hogy ugyanazzal a sorszámmal egyszerre két ember tűz ki feladatot. Ennek azonban nincs túl nagy jelentősége, a feladat sorszámozás is tökéletesen jó módszer.)
|
|
|
| [2383] Csimby | 2007-10-14 22:42:52 |
 (a 126.feladatra gondolsz? ;-))
A megoldását mondjuk nem találtam meg. A sajátomnak tudom, csak arra lennék kíváncsi hogy lehet-e valahogy egyszerűbben, mert én mint geometria feladatot "kiszámoltam".
|
| Előzmény: [2382] Lóczi Lajos, 2007-10-14 20:28:59 |
|
| [2384] Csimby | 2007-10-14 22:45:28 |
 Hivatkozni tényleg jobb úgy. De azért az nem rossz ha látszik egy hozzászóláson hogy ez most új feladat, vagy csak a 20.hozzászólás valamihez. A könyvekben is vannak fejezetek, noha az oldalszám alapján egyszerűbben lehet hívatkozni.
|
| Előzmény: [2381] jonas, 2007-10-14 16:36:28 |
|
| [2385] jonas | 2007-10-14 23:26:45 |
 Én is csak kiszámolni tudnám (noha nem egyértelmű, hogy a legegyszerűbb kiszámolni).
Az eredeti koordinátarendszerben a grafikon azon (x,y) pontok halmaza, amire y2=x. A forgatás az (u,v) pontot az 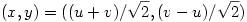 pontból kapja. Ebből pontból kapja. Ebből 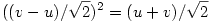 , amiből , amiből 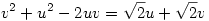 , azaz , azaz 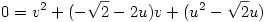 . Ez másodfokú, megoldva (nyilván a nagyobbik megoldás kell) . Ez másodfokú, megoldva (nyilván a nagyobbik megoldás kell) 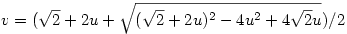 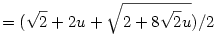 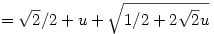
Azt előre tudjuk, hogy a megoldás egyszerű alakú lesz, mert egy kúpszelet elforgatva is kúpszelet.
|
| Előzmény: [2383] Csimby, 2007-10-14 22:42:52 |
|
| [2386] Csimby | 2007-10-15 00:47:27 |
 Köszi! Nekem is majdnem ez jött ki, csak a vége: 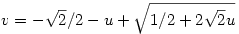 Ami azért tűnik jobbnak, mert u=0-ra v=0 jön ki. Én úgy csináltam, hogy (x,x) pontból merőlegest állítottam x=y-ra, ennek és Ami azért tűnik jobbnak, mert u=0-ra v=0 jön ki. Én úgy csináltam, hogy (x,x) pontból merőlegest állítottam x=y-ra, ennek és 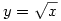 -nek a metszéspontja legyen (y,y2). És akkor a fv. amit keresünk, az |(x,x)|-hez rendeli (y,y2) és (x,x) távolságát. De kb. ugyanilyen gyorsan kijön, mert lehet találni egy egyenlőszárú derékszögű háromszöget. Ez lehet hogy elsőre csúnyának tűnik, de hamar kijön ezzel is. -nek a metszéspontja legyen (y,y2). És akkor a fv. amit keresünk, az |(x,x)|-hez rendeli (y,y2) és (x,x) távolságát. De kb. ugyanilyen gyorsan kijön, mert lehet találni egy egyenlőszárú derékszögű háromszöget. Ez lehet hogy elsőre csúnyának tűnik, de hamar kijön ezzel is.
|
| Előzmény: [2385] jonas, 2007-10-14 23:26:45 |
|
| [2387] Cckek | 2007-10-18 21:48:34 |
 Egy számotokra, tisztelt fórumozók, egyszerű, ugyanakkor nagyon kedves kis feladat:
A táblára fel van rajzolva 999 piros, 1000 fehér és 1001 zöld kör. A következő műveletet végezzük: letörlünk két különböző színű kört és helyette rajzolunk egy olyat amilyent nem töröltünk. Milyen színű kör marad végül a táblán?
|
|
| [2388] Hajba Károly | 2007-10-18 23:52:58 |
 A művelet végzése során mindhárom halmaz és az összhalmaz paritása is az ellenkezőjére fordul. Azaz mindig lesz egy halmaz, melynek a paritása mindig megegyezik az összhalmaz paritásával. Ez akkor sem változik, mikor a másik két halmaz már üres. Ez akkor működik így, ha a három halmaz paritásaiban van különböző.
Jelen példánál az összhalmaz paritása páros, ezért páratlan fehér kör marad meg.
Valóban érdekes kis feladat.
|
| Előzmény: [2387] Cckek, 2007-10-18 21:48:34 |
|
| [2389] Cckek | 2007-10-19 07:30:31 |
 Igen, a bizonyítás tökéletes. A gyerekek számára viszont elég nehezeknek tűnnek ezek az invariánsok elvére épülő feladatok. Itt van még egy:
Adott a síkban az A(x,y) kordinátájú pont. A következő kordinátájú pontokba léphetünk:
(x+1,y+1),(x-1,y+1),(x-1,y-1),(x+1,y-1).
Bizonyítsuk be, hogy az origóból nem juthatunk el a (2007,2008) kordinátájú pontba.
|
| Előzmény: [2388] Hajba Károly, 2007-10-18 23:52:58 |
|
| [2390] HoA | 2007-10-19 16:42:01 |
 A feladatban szereplő egyesszámú kérdés: "Milyen színű kör marad végül a táblán?" és a több kört megengedő válasz: "páratlan fehér kör marad meg" felveti a feladat folytatásának lehetőségét:
a) 2k+1 , 2l, 2m+1 különböző színű körből indulva biztos-e, hogy végül 1 db. kör marad?
Ha nem, akkor
b) 2k+1 , 2l, 2m+1 különböző színű körből indulva van-e olyan stratégia, mellyel végül 1 db. kör marad?
|
| Előzmény: [2388] Hajba Károly, 2007-10-18 23:52:58 |
|
| [2391] Gyöngyő | 2007-10-20 15:49:02 |
 Sziasztok!
Nekem is lenne egy kérdésem egy másik feladattal kapcsán:
Adva van P és Q hermetikus idempotens mátrix,ugyanaz a dimenziójuk és a rangjuk is. Bizonyítsuk be,hogy ha P*Q*P=P,akkor P=Q.
Üdv: Gyöngyő
|
|
|
|
|
| [2395] Gyöngyő | 2007-10-21 11:58:43 |
 mátrix szorzásról van szó.
üdv.Gyöngyő
|
|
|
| [2397] Gyöngyő | 2007-10-21 18:39:08 |
 Sziasztok! A hermitikus mátrix az az jeleti,hogy komplex elemű!
Üdv:
Gyögyő
|
|
|
| [2399] Lóczi Lajos | 2007-10-22 12:32:28 |
 Egyelőre csak a következőt sikerült igazolnom: P=PQ=QP.
Jelölések: a mátrixszorzást az egymás mellé írás, a csillag a konjugált transzponáltját jelentse szokás szerint.
Feltétel szerint P2=P=P* és Q2=Q=Q*. (Ezek a vetítőmátrixok, vagy projektorok egyébként.)
Legyen A=PQ-P és számoljuk ki AA*-ot:
AA*=(PQ-P)(PQ-P)*=(PQ-P)(Q*P*-P*)=(PQ-P)(QP-P)=PQP-PQP-PQP+P=0, mert tudjuk, hogy P=PQP. De ismert, hogy AA*=0 maga után vonja, hogy A=0, azaz P=PQ. Véve ennek transzponált-konjugáltját, kapjuk, hogy P=P*=(PQ)*=Q*P*=QP.
(Nyilván a rangfeltételt nem használtam még fel, ez kellhet a továbbhaladáshoz.)
|
| Előzmény: [2391] Gyöngyő, 2007-10-20 15:49:02 |
|
| [2400] Lóczi Lajos | 2007-10-22 18:07:19 |
 arxiv.org/pdf/math.RA/0003224.pdf
Ez egy 220 oldalas dokumentum, témája a projektorok rangjainak kiszámítása, kicsit nézegettem, de sajnos nem találtam benne jó formulát (bár nagyon hasonlókat igen), hátha ez segít...
|
| Előzmény: [2399] Lóczi Lajos, 2007-10-22 12:32:28 |
|
| [2401] Lóczi Lajos | 2007-10-22 22:14:07 |
 Ha P projektor, akkor nyilván P(I-P)=(I-P)P=0, ahol I az identitás(mátrix).
A rangfeltételt figyelembe véve ezt az állítást kellene megfordítani, ebből a feladat már következne, vagyis elegendő volna igazolni, hogy
"Ha [rangfeltétel teljesül] és PR=RP=0, akkor R=I-P."
Itt persze az R:=I-Q választásra gondolok (az előzőekben ugyanis láttuk, hogy P(I-Q)=(I-Q)P=0 valóban teljesül).
|
| Előzmény: [2399] Lóczi Lajos, 2007-10-22 12:32:28 |
|
| [2402] Cckek | 2007-11-02 03:12:42 |
 oldjuk meg a funkcionalegyenletet:
f(x)=(x-y)f((x-y+1)x)+f(y)
|
|
|
| [2404] Zsolt21 | 2007-11-04 12:19:07 |
 Üdv. mindenkinek! Én még új vagyok itt a fórumon, és lenne 1 feladványom (remélem még nem volt): Zsófi tegnapelőtt 10 éves volt, jövőre 13 lesz.Mikor született?
|
|
| [2405] Pardeller | 2007-11-04 12:23:35 |
 Ha jól értem a feladatot, akkor tegnaphoz 11 éve ;)
Emlékszem, hogy valamikor láttam itt a fórumon a következő feladat megoldását, de nem találom. Előre is köszönöm, ha valaki oda tud irányítani, vagy le tudja esetleg újból írni a megoldást:
Bizonyítsuk be, hogy egy egész oldalhosszúságú négyzet nem bontható fel maradéktalanul nála kisebb, különböző egész oldalhosszúságú négyzetekre.
|
|
|
|
|
| [2409] Pardeller | 2007-11-04 15:21:27 |
 Hmm, furcsa... lehet, hogy kockákkal volt? most már nem vagyok túl biztos benne :S
|
|
|
|
|
|
|
|
|
| [2417] kertitorpe | 2007-11-10 19:12:29 |
 Üdvözletem!
Van egy érdekes feladatom:
Pontosan mivel egyenlő az alábbi kifejezés?
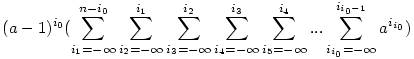 , ahol , ahol
a , n >1; n és minden ij egész
|
|
|
| [2419] Bubóka | 2007-11-11 20:11:38 |
 Érdekes feladat: Rajzolj csak körző segítségével adott körbe négyzetet, a lehető legkevesebb lépésből.
|
|
| [2420] Hajba Károly | 2007-11-12 00:04:43 |
 No te hány lépésből tudod? 10, talán 8 vagy esetleg még ennél is kevesebb? :o)
Kiváncsi vagyok a te verziódra is. De már volt itt téma többször is. Ha nem találod, szólj, megmutatom.
|
| Előzmény: [2419] Bubóka, 2007-11-11 20:11:38 |
|
|
| [2422] jonas | 2007-11-12 18:01:24 |
 Kíváncsi lennék, mi van megadva, és mi számít lépésnek. Pl. a kör középpontja adott-e, egy pont a kör kerületén ki van-e jelölve, vagy az is egy lépés.
|
| Előzmény: [2421] Bubóka, 2007-11-12 14:13:50 |
|
| [2423] Bubóka | 2007-11-12 19:01:38 |
 Adott a kör és egy pont.
Van még egy érdekesnek tűnő feladat, amivel nem tudok mit kezdeni, de megoldható: Adott egy kör , keressük meg a középpontját csak körzővel!! ???
|
| Előzmény: [2422] jonas, 2007-11-12 18:01:24 |
|
|
| [2425] Maga Péter | 2007-11-13 19:23:13 |
 Minden, ami szerkesztheto korzovel es vonalzoval, az szerkesztheto csak korzovel is. Lenyegeben ez a Mohr-Masceroni-tetel allitasa, a bizonyitas egyebkent meg is adja a szerkesztes lepeseit. Erdemes megtanulni az inverziot es azzal meg lehet csinalni a tetelt, egyuttal a feladatot is. Szoval hajra!
|
| Előzmény: [2423] Bubóka, 2007-11-12 19:01:38 |
|
| [2426] Python | 2007-11-14 18:00:42 |
 Ezt a feladatot egy barátomtól hallottam: Nevezzünk egy prímet érdekesnek, ha az elejéről vagy a végéről (egyszerre csak az egyik irányból) néhány jegyet elhagyva mindig prímet kapunk (10-es számrendszer)! Létezik-e végtelen sok érdekes prím?
Az ábrán egy 4-jegyű érdekes prím látható:
|
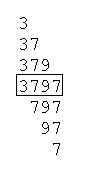 |
|
| [2427] Róbert Gida | 2007-11-14 18:35:23 |
 Véges sok van beőlük, sőt már azokból is, amikor csak az egyik irányból követeled meg ezt (balról haladva csak akkor, ha felteszed, hogy a számban nincsen 0 jegy). Trunctable prime kifejezésre keress rá, elég közismert probléma. A te kérdésedre a válasz, csak ezek a megoldások vannak: 2, 3, 5, 7, 23, 37, 53, 73, 313, 317, 373, 797, 3137, 3797, 739397 Ami egyébként: http://www.research.att.com/ njas/sequences/A020994.
|
| Előzmény: [2426] Python, 2007-11-14 18:00:42 |
|
|
| [2429] nemtommegoldani | 2007-11-15 18:43:44 |
 Sziasztok!Két matekfeladatom lenne, amit nme tudok megoldani, ebben szorulnék segítségre. 1. Bizonyítsd be indirekt úton, hogy a kettes alapú log3 irracionális szám! 2. Az ABC háromszög mely belső P pontja esetén lesz az a/x+b/y+c/z összeg minimális?(a,b,c a háromszög oldalai, x,y,z a P pontnak az oldalaktól való távolsága). A segítséget nagyon szépen köszönöm.
|
|
| [2430] SmallPotato | 2007-11-15 19:03:50 |
 Az elsőhöz:
Tegyük fel, hogy 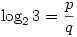 , ahol p és q egészek. , ahol p és q egészek.
Ekkor 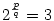 , ahonnan 2p=3q, ami azonban lehetetlen, mert a baloldal csupa 2-es, a jobboldal viszont csupa 3-as törzstényező szorzatából áll. Ezek szerint log23 nem írható fel , ahonnan 2p=3q, ami azonban lehetetlen, mert a baloldal csupa 2-es, a jobboldal viszont csupa 3-as törzstényező szorzatából áll. Ezek szerint log23 nem írható fel 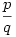 alakban. alakban.
|
| Előzmény: [2429] nemtommegoldani, 2007-11-15 18:43:44 |
|
|
|
| [2433] kisevet7 | 2007-11-21 20:48:07 |
 Tudna valaki segíteni??? A feladatom a következő: x(t) és y(t) két hadsereg létszáma. A veszteség létszáma x'(t)=-a*y(t). (a állandó)Vizsgáljuk mekkora x(0), y(0) értékeknél ki fog győzni! (Számpélda: Napóleon serege 200000 fő, Háry Jánosé 200 fő, és tudjuk, hogy Háry győzött. Mennyivel hatékonyabb egy huszár, mint egy francia?) Előre is köszönöm a segítséget! kisevet
|
|








 0, akkor az additív inverzre fordított reláció áll fenn. Valóban: 0=x+(-x)
0, akkor az additív inverzre fordított reláció áll fenn. Valóban: 0=x+(-x) 0, akkor a fentiek alapján x.x=(-x)(-x) és most 3/2-es axióma.
0, akkor a fentiek alapján x.x=(-x)(-x) és most 3/2-es axióma.  0, így a > definíciója miatt 1>0.
0, így a > definíciója miatt 1>0.  Pozitív. (Nincsen akkor-és-csak-akkor nyíl?) Ahol a Pozitív halmaz halmaz definíciójára már nem emlékszem, de talán lehet azon Q-beliek halmaza melyek előállnak (1+1+...+1)/(1+1+...+1) alakban. Ez nyilván működik Z-ben is. Hogy R-ben ezt hogy lehetne megoldani, azt nem tudom, lehet hogy nem is lehet. És ha így definiáltuk, akkor 1>0-n nincs mit bizonyítani. Persze elegánsabb és számomra nagyon tanulságos volt amit te írtál, hogy, felvesszük a rendezés axiómáit is és azt mondjuk, hogy a>b acsa. a
Pozitív. (Nincsen akkor-és-csak-akkor nyíl?) Ahol a Pozitív halmaz halmaz definíciójára már nem emlékszem, de talán lehet azon Q-beliek halmaza melyek előállnak (1+1+...+1)/(1+1+...+1) alakban. Ez nyilván működik Z-ben is. Hogy R-ben ezt hogy lehetne megoldani, azt nem tudom, lehet hogy nem is lehet. És ha így definiáltuk, akkor 1>0-n nincs mit bizonyítani. Persze elegánsabb és számomra nagyon tanulságos volt amit te írtál, hogy, felvesszük a rendezés axiómáit is és azt mondjuk, hogy a>b acsa. a






 142857 (b=1)
142857 (b=1)
 k(mod10k-1), de ekkor 10m+1
k(mod10k-1), de ekkor 10m+1

 n!/e, hiszen a 0. és első tag összege: (-1)0/0!+(-1)1/1!=1-1=0, tehát tényleg elég a 2. tagtól összegezni.
n!/e, hiszen a 0. és első tag összege: (-1)0/0!+(-1)1/1!=1-1=0, tehát tényleg elég a 2. tagtól összegezni.
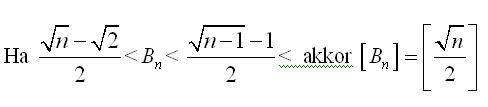
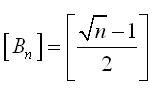
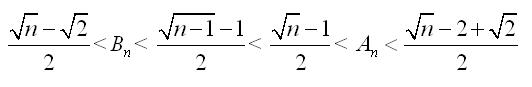

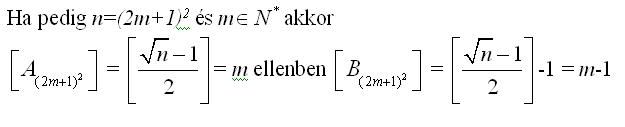
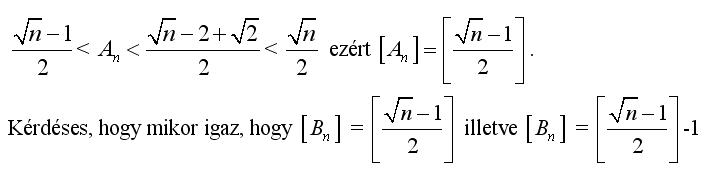

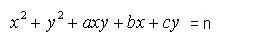

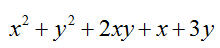
 m,n
m,n