| [1030] nadorp | 2005-08-18 09:44:25 |
 Ez egy számolós megoldás. Szerintem van tisztán kombinatorikai is, vagy valami polinomiális tételes is, ezt egyelőre nem találtam. Jelöljük a kifejezést A-val. Ekkor
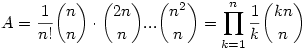 Itt minden tényező egész, ui. Itt minden tényező egész, ui.
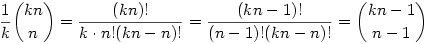
|
| Előzmény: [1025] Yegreg, 2005-08-16 22:48:40 |
|
|
|
| [1027] Lóczi Lajos | 2005-08-17 21:33:21 |
 Kiküszöbölve az egyenletekből pl. x-et és y-t, z-re az alábbi egyenletet kapjuk:
4z8+230z6+81297z4+41720z2+71824=0.
Erről az egyenletről viszont világosan látszik, hogy nincs valós megoldása, csak komplex, tehát az eredeti egyenletrendszernek sincs valós megoldása.
|
| Előzmény: [1026] xviktor, 2005-08-17 18:38:28 |
|
| [1026] xviktor | 2005-08-17 18:38:28 |
 191. Feladat: Oldjuk meg a kovetkezo egyenletrendszert a valos szamok halmazan:
1.:x2+y2-xy=225
2.:x2+z2-xz=121
3.:y2+z2-yz=36
Jo gondolkodast: Viktor
U.i.: Hogy lehet megcsinalni, hogy a 3. egyenlet a tobbi alatt legyen?
|
|
| [1025] Yegreg | 2005-08-16 22:48:40 |
 Én nem feltétlenül tekinteném különböző megoldásnak, annyi, hogy én felbontottam a szab. háromszöget 3 egyenlószárú háromszögre. Itt egy feladat, ezt nem én találtam ki, csak hallottam, és tetszett, talán azért, mert egész gyorsan megoldottam:)
Bizonyítsuk be, hogy az 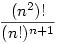 kifejezés bármely n (nyilván természetes szám) esetén egész! Több megoldást is lehet adni rá! kifejezés bármely n (nyilván természetes szám) esetén egész! Több megoldást is lehet adni rá!
Üdv:
Yegreg
|
|
| [1024] Lóczi Lajos | 2005-08-16 19:10:57 |
 Szép megoldás!
(Egy TeX-es megjegyzés a környező feladatokhoz: amikor koszinuszt/szinuszt írtok be, használjátok a "backslash"-t előtte, így olyan formátumot kapunk, ahogyan a könyvekben szokás: cos x-et, és nem cosx-et, ami utóbbi a c, o és s változók szorzata szokott lenni. Hasonló igaz a többi beépített függvénynévre is, pl. log x és nem logx.)
|
| Előzmény: [1021] xviktor, 2005-08-16 17:17:14 |
|
| [1023] xviktor | 2005-08-16 18:22:24 |
 Jo a megoldasod mutatok egy masikat is...
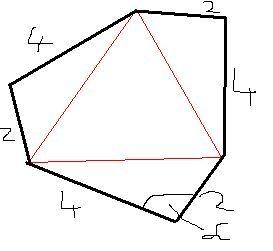
A forgasszimmetria miatt:
1.: A belso haromszog egy szabalyos haromszog, melynek terulete: 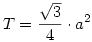
2.: A 3 kis haromszog egybevago. Felirtam a cosinus tetelt egy kis haromszogre: a2=22+42-2.2.4.cos =20-16cos =20-16cos
1-2bol: 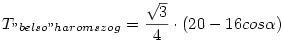
A kis haromszogek terulete /mindharome osszesen/: 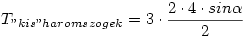
Igy a hatszog terulete: 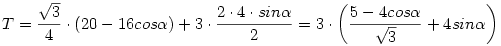
|
 |
| Előzmény: [1022] Yegreg, 2005-08-16 17:36:10 |
|
| [1022] Yegreg | 2005-08-16 17:36:10 |
 A hatszöges feladatra írt képlet így jött ki: Vagyünk 3 szomszédos csúcsot, és a két szélsőt kössük össze a 120°-os forgásszimmetria középpontjával. Ekkor a forgásszimmetria miatt(bármelyik 3 egymás melletti csúcsot választjuk) a hatszög területének 3-ada lesz a kapott négyszög területe. Ez eddig a külső 3-as szorzó, a zárójelben a négyszög területe van. A négyszög oldalai: 2, 4, a, a. Az első kettő a hatszög két oldala a másik kettő a szimmetria miatt egyenlő. Kössük össze egymással a két szélső pontot, ekkor a négyszög egy átlóját kapjuk, ami két háromszögre bontja a négyszöget, a külső egyértelműen meghatározott adott  belső szögnél, hiszen két oldal és a közbezárt szög ismert, és ebből a belső háromszög is meg lett határozva, hiszen az egyik oldala a külsővel közös, a rajta fekvő szögek pedig nyilván 30°-osak. A külső háromszög területe ekkor belső szögnél, hiszen két oldal és a közbezárt szög ismert, és ebből a belső háromszög is meg lett határozva, hiszen az egyik oldala a külsővel közös, a rajta fekvő szögek pedig nyilván 30°-osak. A külső háromszög területe ekkor
t1=4sin
. A behúzott átló legyen b! Ekkor b2=22+42-16cos a koszinusz tétel alapján. Ha behúzzuk a belső háromszög magasságát, akkor két egybevágó félszabályos háromszöget kapunk, ahol a nagyobb befogó a koszinusz tétel alapján. Ha behúzzuk a belső háromszög magasságát, akkor két egybevágó félszabályos háromszöget kapunk, ahol a nagyobb befogó 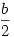 , a kisebb pedig így , a kisebb pedig így  , ami a belső háromszög magassága. A belső háromszög területe tehát , ami a belső háromszög magassága. A belső háromszög területe tehát

(valóban egyszerűsíthetünk). A hatszög területe pedig:
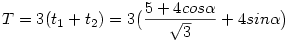
Ennyi. Üdv:
Yegreg
|
|
| [1021] xviktor | 2005-08-16 17:17:14 |
 A 189. feladat megoldasa szerintem:
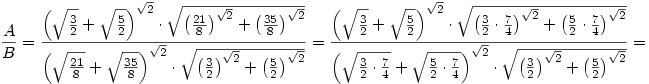
![=\frac{{\left(\sqrt{\frac32}+\sqrt{\frac52}\right)^{\sqrt2}\cdot \sqrt{\left(\frac74\right)^{\sqrt2}\cdot \left[\left(\frac32\right)^{\sqrt2}+\left(\frac52\right)^{\sqrt2}\right]}}}{{\left[\sqrt{\frac74}\cdot\left(\sqrt{\frac32}+\sqrt{\frac52}\right)\right]^{\sqrt2}\cdot \sqrt{\left(\frac32\right)^{\sqrt2}+\left(\frac52\right)^{\sqrt2}}}}=\frac{{\left(\sqrt{\frac32}+\sqrt{\frac52}\right)^{\sqrt2}\cdot \sqrt{\left(\frac32\right)^{\sqrt2}+\left(\frac52\right)^{\sqrt2}}}\cdot\sqrt{\left(\frac74\right)^{\sqrt2}}}{{\left(\sqrt{\frac74}\right)^{\sqrt2}\cdot\left(\sqrt{\frac32}+\sqrt{\frac52}\right)^{\sqrt2}\cdot \sqrt{\left(\frac32\right)^{\sqrt2}+\left(\frac52\right)^{\sqrt2}}}}=1](keplet.cgi?k=DF34C505BB17548F)
Eszreveheto, hogy az egyszerusitesek utan 1et kapunk. Igy A=B.
Amennyiben valamit elirtam legyszives szoljatok, es kijavitom.
Remelem jo a megoldasom: Viktor
|
| Előzmény: [1020] Lóczi Lajos, 2005-08-16 15:00:38 |
|
| [1020] Lóczi Lajos | 2005-08-16 15:00:38 |
 A különböző gyökkitevők egy összegben felcserélhetők?
189. feladat. Jelölje
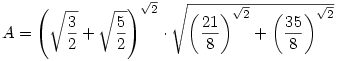
és
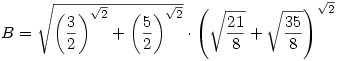
Döntsük el (majd bizonyítsuk be), hogy kettejük közül melyik a nagyobb szám.
|
|
| [1019] Lóczi Lajos | 2005-08-16 14:48:19 |
 Aki szeret térfogatot számolni, annak álljon itt a
188. feladat. Legyen a>0 adott szám és tekintsük a közönséges térbeli x-y-z koordinátarendszert.
Mekkora a térfogata annak a testnek, amely az x2+y2+z2 4a2 egyenlőtlenséggel meghatározott gömb és az (x-a)2+y2 4a2 egyenlőtlenséggel meghatározott gömb és az (x-a)2+y2 a2 (végtelen) henger metszeteként áll elő? a2 (végtelen) henger metszeteként áll elő?
|
|
|
|
| [1016] xviktor | 2005-08-15 23:28:27 |
 Annyibban igazad van, hogy tobb eset van, tehat egy altalanos kepletet keresunk, de szerintem nem jo a kepleted... bar lehet en tevedek
Es akkor a 187. feladat: a hatszog kore kor irhato. Mekkora a terulete?
Udv: Viktor
|
| Előzmény: [1015] xviktor, 2005-08-15 23:14:22 |
|
|
| [1014] Yegreg | 2005-08-15 21:01:22 |
 Bocsánat, úgy tűnik, hogy most sem vagyok képes normálisan beírni... egy zárójel elcsúszott. Helyesen így:
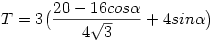
. Hiába, még nem vagyok rutinos TeX-es...:oD. Üdv:
Yegreg
|
|
| [1013] Yegreg | 2005-08-15 20:58:07 |
 Üdv!
Bocs, hogy csak most írok, de most értem haza, így nem tudtam reagálni a közbenső dolgokra. A beírt gömb sugara jogos, az egyenletet nem ismertem, kitalálni meg akkor este esélyem sem volt, pláne, hogy nem is gondolkoztam ilyesmiben(a bizonyítás amúgy nagyon szép szerintem). A sok számolás azért nem annyira sok, csak egy finom túlzás volt annak eltitkolása érdekében, hogy képtelen lettem volna beírni akkor este:). Valójában azt hiszem, hogy az pár Pitagorasz-tétel volt.
Az a hatszöges feladat nem akar összejönni Viktornak:) Vagy direkt csináltad először nem létezőre másodjára pedig több esetesre? Szóval a 186(azt hiszem) feladat megoldása:
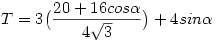
Ahol alfa valamelyik belső szög. A 120°-os forgásszimmetria nem határozza meg egyértelműen a hatszöget, csak 3-3 belső szöge egyenlő egymással, két különböző belső szög összege pedig 240°. Egyébként szerintem a feladat normálisan körbe írt hatszög lenne. Akkor egyértelműen  =120°, és akkor kiszámolható a terület(akkor máshogy is számolható). Üdv: =120°, és akkor kiszámolható a terület(akkor máshogy is számolható). Üdv:
Yegreg
|
|
| [1012] xviktor | 2005-08-14 17:59:30 |
 Gratulalok, mindenki megoldasa helyes. De a 186. feladatra meg nem jott megoldas...
Jo gondolkozast: Viktor
|
|
| [1011] lorantfy | 2005-08-14 16:26:14 |
 185-höz: Kössük össze a poliéder csúcsait a beírt gömb középpontjával. Így a poliéder térfogatát sokszög alapú gúlák térfogatának összegére bontottuk, melyek magassága éppen a beírt kör sugara, alapjaik területének összege pedig a poliéder felszine.
Igy aztán: 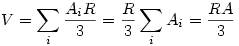
|
| Előzmény: [1010] xviktor, 2005-08-13 01:19:00 |
|
| [1010] xviktor | 2005-08-13 01:19:00 |
 Gratulalok szepek a megoldasaid /181,182,183/, a 184-et meg atgondolom en kicsit maskepp csinaltam,de szerintem az is jo.
A 183. feladatnal irtad hogy sok szamolas volt, pedig nagyon egyszeruen meg lehet allapitani a beirt gomb sugarat:
Tetel: Barmely poliederbe beirt gomb sugara: 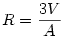
185. feladat: Bizonyitsuk be a fenti tetelt.
186. feladat: A 181. feladatot kisse fogalmazzuk at. Ha ahelyett hogy kor irhato bele azt mondanam, hogy 120°os forgasszimmetrikus, akkor mekkora lenne a terulete? /Ilyen hatszog letezik ;-)/
Jo gondolkodast: Viktor
|
| Előzmény: [1009] Yegreg, 2005-08-13 00:49:02 |
|
| [1009] Yegreg | 2005-08-13 00:49:02 |
 181.:
Ilyen hatszög nem nagyon van, hiszen ha egy 2 egység hosszú oldalt a kör x-re és 2-x-re bont, akkor az az x melletti 4 egység hosszú oldalt x-re és 4-x-re bontja, hiszen a körhöz külső pontból húzott érintő szakaszok egyenlőek, illetve továbblépve a 4-x melletti 2 egység hosszú oldalra, azt a körnek 4-x és 2-(4-x)-re kell bontania, szintén az érintő szakaszok miatt, azonban 2-(4-x)=x-2, csak akkor pozitív, ha x nagyobb, mint kettő, x azonban nem lehet nagyobb kettőnél, mert akkora szakaszt metszett le a kör egy másik két egység hosszú oldalból, tehát ha a beírt kör nem mehet át csúcson(azaz azt a sokszög teljes egészében tartalmazza), akkor nincs ilyen hatszög.
182:
20 3-as maradéka 1, 21-é 2, és belátható, hogy innentől kezdve periodikus, hiszen a 2 kétszerese mindig 4, aminek a 3-as maradéka mindig egy, az 1 kétszerese pedig mindig 2, aminek a 3-as maradéka kettő, ezzel a ciklus végére értünk. Látható tehát, hogy minden páratlan kitevő esetén 2 a hármas maradék. A 2333+2555-1 esetében a két kettő hatvány kitevője páratlan, hármas maradékuk 2 és 2, ezek összege 4, mínusz egy az 3, tehát az összeg osztható 3-mal, és mivel nagyobb nyilván, mint három, így nem lehet prím.
183:
Sok számolgatással(amit most nem szeretnék leírni, mert úgyis félreírnám) megkapjuk, hogy szabályos tetraédernél:
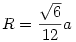
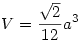

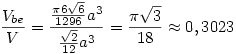
184:
Ha összekötjük a négy alsó gömb középpontját a vele szomszédosokkal, valamint az alsó 4-ét a felsőjével, akkor egy négyzet alapú gúlát kapunk, aminek minden oldala R.(ezt be lehet látni, hiszen érintik egymást) Ennek a gúlának a magassága 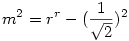 (Pitagoras tétel alapján) (Pitagoras tétel alapján)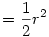 Ebből Ebből  Amiből ha meg akarjuk kapni a földtől való tárvolságot, akkor még hozzá kell adni Amiből ha meg akarjuk kapni a földtől való tárvolságot, akkor még hozzá kell adni 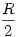 , hiszen a gúla ilyen magasan van, ekkor tehát az 5. gömb távolsága a talajtól: , hiszen a gúla ilyen magasan van, ekkor tehát az 5. gömb távolsága a talajtól:

És azt hiszem, ennyi feladat volt. Bocsánat, hogy 1, nincs ábra 2, nincs túl sok számolás leírva 3, ha valahol számolási hibát vétettem , de késő van már.
Üdv:
Yegreg
|
|
| [1008] xviktor | 2005-08-12 16:41:51 |
 Mostanaban hallottam par jo kis feladatot, gondoltam beirok ide parat.
181. feladat: Van egy hatszog mely oldalai: 2,4,2,4,2,4 /ebben a sorrendben/. Mekkora a hatszog terulete, ha tudjuk, hogy kor irhato bele?
182. feladat: Kicsit maskepp irom be ide mint az eredeti feladatban szerepel, hogy szamologepet ne lehessen hasznalni: Bizonyitsuk be hogy 2333+2555-1 nem prim!
183. feladat: Van egy szabalyos tetraederunk. A tetraederbe irt gomb terfogata hany szazaleka a tetraeder terfogatanak?
184. feladat: Van negy ugyanakkora sugaru gomb, melyek egy vizszintes asztalon paronkent erintik egymast. Pontosan kozepre "felrakunk" egy 5., a lentiekkel megegyezo sugaru gombot. Milyen messze van a fenti gomb kozeppontja a talajtol?
Jo gondolkodast!
|
|
|
|





 =20-16cos
=20-16cos
 4a2 egyenlőtlenséggel meghatározott gömb és az (x-a)2+y2
4a2 egyenlőtlenséggel meghatározott gömb és az (x-a)2+y2
