|
|
|
|
|
| [1127] Lóczi Lajos | 2005-11-14 19:31:31 |
 Ami alatt azt érted nyilván, hogy az ember ilyenekkel nem sokra megy, hiszen az egyik végtelen szorzatot átkonvertálja egy ki nem számítható integrálba, illetve végtelen összegbe. :)
Inkább érdekesebbek pl. a becslések. Hagyjuk el a gyököt az egyszerűség kedvéért. Egy lehetséges approximáció, pl. 5-nél kettébontva:
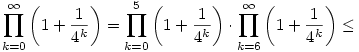
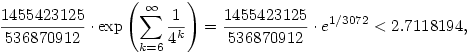
felhasználva, hogy 1+x ex minden valós x-re, továbbá a mértani sor összegképletét. ex minden valós x-re, továbbá a mértani sor összegképletét.
Egy alsó becslés pl.
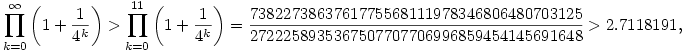
használva a monoton növekedést.
|
| Előzmény: [1125] Róbert Gida, 2005-11-14 16:50:59 |
|
| [1125] Róbert Gida | 2005-11-14 16:50:59 |
 Zsabóka végtelen szorzatos feladatához: Nyilván elég i=1-től menni és a négyzetét vizsgálni, mert ha ez megvan, akkor könnyen megkapható az eredeti szorzat is. De ez éppen http://mathworld.wolfram.com/InfiniteProduct.html oldalon található 43. formula spec. esete n=4-re. Nem tudom erre gondoltál-e. Nem a legszebb formula.
|
|
| [1124] nadorp | 2005-11-14 14:33:37 |
 Ezt sajnos elszámoltam, pontosabban az elv volt rossz.Ez a feladat összefügg a számok partícióinak a számával, én meg sajnos csak a kéttagú partíciókat vettem.A végeredmény az enyémnél több lesz.
|
| Előzmény: [1123] Zsabóka, 2005-11-14 13:34:46 |
|
| [1123] Zsabóka | 2005-11-14 13:34:46 |
 Itt aztán gyorsan lebukik az ember -), hiba került a feladatba. Igazából:
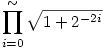
lett volna a feladat. Ettöl perzse semmi nem lett könnyebb. De hogy jutottál az
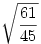
alakra ? Ez alapján az eredmény
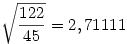
lenne.
|
| Előzmény: [1122] nadorp, 2005-11-14 13:17:59 |
|
|
|
| [1120] Zsabóka | 2005-11-14 12:20:17 |
 Keresett a következö szorzat értéke:
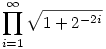
Van esetleg valami köze PI-hez, e-hez ( a négyzete majdnem e )?
|
|
|
| [1118] lorantfy | 2005-11-13 17:25:49 |
  i, i, j, j, k-n kívül van még megoldás? k-n kívül van még megoldás?
Én már majdnem elfelejtettem mik ezek a kvaterniók, így hála Neked, most utána néztem.
A komlex számfogalom 4 dimes kiterjesztéséről van szó:
Ferde testekre ( ferde az olyan test, melyben a szorzás nem kommutatív ) az egyik legfontosabb példa a kvaterniók teste.
Az a+ib+jc+kd alakú kifejezéseket kvaternióknak nevezzük, ahol a,b,c,d tetszőleges valós számokat jelölnek az i,j,k szimbólumokra pedig teljesülnek az alábbi azonosságok
(I) i2=j2=k2=-1,
(II) ij=k, jk=i, ki=j, ji=-k, kj=-i, ik=-j.
Kvaterniókra az összeadást az alábbi egyenlőség definiálja:
(a+ib+jc+kd)+(a`+ib`+jc`+kd`)=(a+a`)+i(b+b`)+j(c+c`)+k(d+d`).
A szorzást úgy végezzük el mint ahogy több tagot szokás többtaggal szorozni, figyelembe véve a (I),(II)-ben szereplő azonosságokat. Test axiómák teljesülése könnyen igazolható. A multiplikatív inverz létezésének igazolása sem nehéz, ha figyelembe vesszük, hogy:
(a+ib+jc+kd)[a+i(-b)+j(-c)+k(-d)]=a2+b2+c2+d2.
|
| Előzmény: [1116] Lóczi Lajos, 2005-11-13 14:24:37 |
|
| [1117] Lóczi Lajos | 2005-11-13 16:09:14 |
 206. feladat. Keressük meg mindazokat a q=a+bi+cj+dk egész kvaterniókat (ahol tehát a,b,c,d valós egészek), melyekre
(2+3i+5j+7k)q=q(2+3i+5j+7k)
teljesül. (Szokás szerint i,j,k jelöli a kvaterniók báziselemeit.)
|
|
| [1116] Lóczi Lajos | 2005-11-13 14:24:37 |
 205. feladat. Oldjuk meg a kvaterniók körében a
q2+1=0
egyenletet!
|
|
| [1115] Lóczi Lajos | 2005-11-13 14:07:37 |
 Egy régi feladat átfogalmazása következzen:
204. feladat. Jelölje a komplex számok alábbi részhalmazát
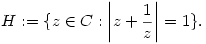
Mutassuk meg, hogy H korlátos. Adjuk meg továbbá azt az origó középpontú körgyűrűt, amely befedi a H halmazt és területe minimális.
|
|
| [1114] Lóczi Lajos | 2005-11-04 21:55:36 |
 203. feladat. Tekintsük a síkon azt a paraméteres görbét, amelyet a
t (2t-sin t,2t+cos t) (2t-sin t,2t+cos t)
hozzárendelés értelmez, ha t [0, [0, ]. Van-e ennek a görbének inflexiós pontja (azaz olyan görbepont, amelyben a görbe érintője "átmetszi" a görbét)? Ha igen, hol? ]. Van-e ennek a görbének inflexiós pontja (azaz olyan görbepont, amelyben a görbe érintője "átmetszi" a görbét)? Ha igen, hol?
|
|
|
| [1112] lorantfy | 2005-11-03 11:53:11 |
 Már indítanám a programot, hogy megkeressem a többi megoldást, de sajnos Pascalban a longint csak 2 milliárdig bírja, így reménytelen a helyzet! :-)
Azért elég jól megmozgatta az emberek fantáziáját ez a feladat. Vagy 50 hozzászólás jött, ami ezzel kapcsolatos.
A Fermat könyv csak ezt az egy ellenpéldát említi az Euler sejtés cáfolataként.
|
| Előzmény: [1110] Lóczi Lajos, 2005-11-02 20:23:27 |
|
| [1111] lorantfy | 2005-11-03 11:36:16 |
 Kedves Lajos!
A megoldásod rendben van. Az én hibám, hogy a feladat kitűzésénél nem fogalmaztam meg, hogy a megoldásnak a sakkal való kapcsolatát keressük.
Írjuk át az egyenletrendszert 2 dimes vektoregyenletre:
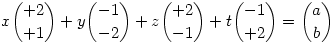
Egy végtelen sakktáblán a (0,0) mezőről el kell jutnunk az (a,b) pontba lólépésben.
|
| Előzmény: [1108] Lóczi Lajos, 2005-11-02 20:15:53 |
|
|
|
| [1108] Lóczi Lajos | 2005-11-02 20:15:53 |
 Nem értem.
"Két egyenletünk van és 4 ismeretlen. Hát miért is ne lenne egész megoldás!"
Íme, egy példa, amikor 1 egyenlet és 4 ismeretlen van, mégsincs megoldás:
2x+2y+2z=2t+1.
Az általam felírt megoldások ekvivalensek az eredeti rendszerrel, tehát annak összes megoldása előállítható a megadott képlettel.
De most már én is kíváncsi vagyok a sakk-kapcsolatra :)
|
| Előzmény: [1107] lorantfy, 2005-11-02 17:03:04 |
|
| [1107] lorantfy | 2005-11-02 17:03:04 |
 Két egyenletünk van és 4 ismeretlen. Hát miért is ne lenne egész megoldás! Nyugodtan megtehetjük, hogy egyik változót lefixáljuk, még akkor is mindig van egész megoldás a többire.
Végülis az az érdekesség benne, ha rájövünk, mi az összefüggés a feladat és a sakk között.
Káli gúlának sikerült! Grat!
|
| Előzmény: [1104] Lóczi Lajos, 2005-11-01 22:43:28 |
|




 ex minden valós x-re, továbbá a mértani sor összegképletét.
ex minden valós x-re, továbbá a mértani sor összegképletét. 


 i,
i, (2t-sin t,2t+cos t)
(2t-sin t,2t+cos t) [0,
[0, ]. Van-e ennek a görbének inflexiós pontja (azaz olyan görbepont, amelyben a görbe érintője "átmetszi" a görbét)? Ha igen, hol?
]. Van-e ennek a görbének inflexiós pontja (azaz olyan görbepont, amelyben a görbe érintője "átmetszi" a görbét)? Ha igen, hol?