| [1466] Lóczi Lajos | 2006-10-31 21:07:22 |
 Egy jópofa feladat:
Adott  valós szám esetén számítsuk ki a valós szám esetén számítsuk ki a 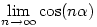 határértéket. határértéket.
|
|
| [1465] Cckek | 2006-10-31 19:52:14 |
 Nos, én is utánnaolvasgattam, úgy tűnik a Jensen egyenlet megoldásai A(x)+a alakúak, ahol A(x) a Cauchy egyenlet megoldása, s mint ilyen lehet nemfolytonos is. Mindenesetre mindkettőtöknek köszönöm a segítségét, megint bebizonyosodott milyen könnyű függvényegyenletet szerkeszteni és milyen nehéz őket megoldani:).
|
| Előzmény: [1462] Lóczi Lajos, 2006-10-31 11:51:03 |
|
| [1464] Lóczi Lajos | 2006-10-31 14:44:53 |
 Igen, a debreceni KLTE-s PDF szép leírás.
Még egy dolog eszembe jutott, már egyszer volt is szó róla itt a fórumon, a hatványsoros megközelítéssel kapcsolatban: tudjuk, hogy vannak 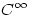 , de nem , de nem 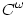 függvények, vagyis olyan függvények, amelyek akárhányszor deriválhatók ugyan, de nem analitikusak, azaz nem fejthetők Taylor-sorba. függvények, vagyis olyan függvények, amelyek akárhányszor deriválhatók ugyan, de nem analitikusak, azaz nem fejthetők Taylor-sorba.
Egy ilyen függvény pl. az f(x):=e-1/x2, ha x 0 és f(0):=0, melyeket szokás "lapos" ("flat") függvényeknek is nevezni. Egyszerűen látható, hogy ennek 0-körüli Taylor-sora a konstans 0 függvény, ami nyilván nem állítja elő f-et semmilyen origó körüli intervallumon sem. 0 és f(0):=0, melyeket szokás "lapos" ("flat") függvényeknek is nevezni. Egyszerűen látható, hogy ennek 0-körüli Taylor-sora a konstans 0 függvény, ami nyilván nem állítja elő f-et semmilyen origó körüli intervallumon sem.
Szóval elvileg ilyen megoldása is lehet egy függvényegyenletnek, ezeket tehát hatványsorfejtéssel nem lehet megtalálni, noha a folytonossággal/deriválhatósággal nincs baj.
|
| Előzmény: [1451] nadorp, 2006-10-30 08:56:12 |
|
|
| [1462] Lóczi Lajos | 2006-10-31 11:51:03 |
 A választ Aczél János vagy Kuczma klasszikus függvényegyenletes könyvei bizonyára tartalmazzák. Az egyenlet neve egyébként Jensen-függvényegyenlet, érdemes megnézni, a neten erről van-e vmi "discontinuous" vagy "nowhere continuous" link, én konkrétat ezalatt a kis idő alatt nem találtam, talán azért, mert a kérdés nagyon klasszikus ízű. Intuitíve biztos vagyok benne, hogy ennek is van millió más megoldása. A konstrukció nyilván Hamel-bázissal kell történjen, a Cauchy-egyenlet mintájára. A megoldásfüggvények grafikonjai ilyen esetben az egész síkon sűrű ponthalmazok szoktak lenni.
|
| Előzmény: [1460] nadorp, 2006-10-31 10:41:56 |
|
|
| [1460] nadorp | 2006-10-31 10:41:56 |
 És mi a helyzet a 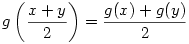 függvényegyenlettel. Feltesszük, hogy pld. x,y>0 ( ez az előző hozzászólásom hiányossága, mert nem zártam ki az x+y=0 lehetőséget az eredeti függvényegyenlet átalakításakor). Van ennek "csúnya" megoldása ? függvényegyenlettel. Feltesszük, hogy pld. x,y>0 ( ez az előző hozzászólásom hiányossága, mert nem zártam ki az x+y=0 lehetőséget az eredeti függvényegyenlet átalakításakor). Van ennek "csúnya" megoldása ?
|
| Előzmény: [1456] Lóczi Lajos, 2006-10-31 09:43:51 |
|
|
|
|
| [1456] Lóczi Lajos | 2006-10-31 09:43:51 |
 Persze ennek a függvényegyenletnek lehet, hogy vannak nemfolytonos, s így nemderiválható megoldásai is, ami lehetetlenné teszi az összes megoldás explicit felírását. (Analógia alapján, a Cauchy-féle f(x+y)=f(x)+f(y) egyenletről jutott eszembe, aminek "csúnya" megoldásából meglehetősen "sok" van.)
|
| Előzmény: [1453] Cckek, 2006-10-30 14:19:43 |
|
| [1455] nadorp | 2006-10-31 09:23:17 |
 Ha f(x)=xg(x), akkor
xg(x)-yg(y)=(x-y)g(x+y)
Azaz tetszőleges t-vel
(x+t)g(x+t)-xg(x)=t.g(2x+t) és
xg(x)-(x-t)g(x-t)=t.g(2x-t) Összeadva
(x+t)g(x+t)-(x-t)g(x-t)=t(g(2x+t)+g(2x-t)) A baloldalra újra alkalmazva az eredeti egyenlőséget:
2t.g(2x)=t(g(2x+t)+g(2x-t)) Bevezetve a 2x+t=p, 2x-t=q jelölést
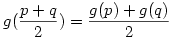 minden p,q valós számra. Ebből úgy néz ki, hogy a függvény konvex és konkáv egyszerre, azaz valószínűleg egyenes. Ha viszont g(x) egyenes, akkor f(x) csak a már megtalált megoldás lehet. minden p,q valós számra. Ebből úgy néz ki, hogy a függvény konvex és konkáv egyszerre, azaz valószínűleg egyenes. Ha viszont g(x) egyenes, akkor f(x) csak a már megtalált megoldás lehet.
|
| Előzmény: [1453] Cckek, 2006-10-30 14:19:43 |
|
| [1454] Yegreg | 2006-10-30 23:56:41 |
 Nem kapcsolódik az aktuális témához, de itt kérdezem meg:
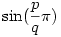 mikor írható fel egész számokkal, alapműveletek és gyökök segítségével? (amúgy elvileg mindig algebrai) mikor írható fel egész számokkal, alapműveletek és gyökök segítségével? (amúgy elvileg mindig algebrai)
Pl: 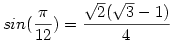
|
|
| [1453] Cckek | 2006-10-30 14:19:43 |
 Ez egy nagyon érdekes következtetés. Ugyanis én valójában az (x+y)(f(x)-f(y))=(x-y)f(x+y)funkcionálegyenletet alakítottam-nem egészen ortodox módon:)-ezzé a differenciálegyenletté. S valóban ennek a funkcionálegyenletnek ezek a függvények a megoldásai.Hogy van-e más is? Jó kérdés:)
|
| Előzmény: [1451] nadorp, 2006-10-30 08:56:12 |
|
|
| [1450] Cckek | 2006-10-29 18:41:57 |
 A következő "differenciálegyenlethez" kellene egy kis segítség: 2xf'(x)=f(2x). Az f(x)=ax illetve f(x)=ax2 függvények megoldások. Van más is?
|
|
|
| [1448] Cckek | 2006-10-29 07:55:26 |
 Nos, nagyon szép bizonyítás, a képletek levezetése nekekem napokba telt.Egy kis korekció, remélem nem fogsz megsértődni érte, az első szumma nem mehet n-ig: 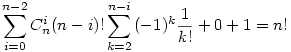
Ahol 0 az n-1 fixponttal rendelkező permutációk száma-tudjuk, hogy ilyen nincs:), 1 az n fixpontal rendelkező permutációk száma, tudjuk hogy ilyen csak egy van az identikus permutáció. Amúgy találtam rá egy egyszerű bizonyítást:
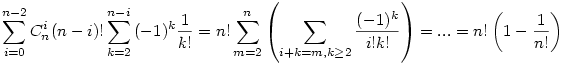
|
| Előzmény: [1447] nadorp, 2006-10-29 01:29:11 |
|
| [1447] nadorp | 2006-10-29 01:29:11 |
 A szita formula egy ismert alkalmazása a következő: Egy színházi előadáson a ruhatárba n darab ernyőt adtak le. Az előadás után senki sem a saját ernyőjét kapta meg. Hányféleképpen történhet meg ez ?
Az eredmény 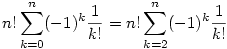
A fenti alapján az 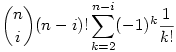 képlet az (1,2,...n) azon permutációinak a száma, amikor pontosan i darab elem van a saját helyén. Ha i=n-1, akkor az összeg 0, hiszen nincs olyan eset, amikor n-1 elem a saját helyén van és 1 meg nem. Ha i=n, a kkor a fenti összeg 1, hiszen minden elem a saját helyén van. Az összes esetek száma az n darab elem permutációinak a száma, azaz n!. Tehát képlet az (1,2,...n) azon permutációinak a száma, amikor pontosan i darab elem van a saját helyén. Ha i=n-1, akkor az összeg 0, hiszen nincs olyan eset, amikor n-1 elem a saját helyén van és 1 meg nem. Ha i=n, a kkor a fenti összeg 1, hiszen minden elem a saját helyén van. Az összes esetek száma az n darab elem permutációinak a száma, azaz n!. Tehát
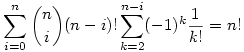
|
| Előzmény: [1442] Cckek, 2006-10-27 22:25:21 |
|
|
|
|
|
| [1442] Cckek | 2006-10-27 22:25:21 |
 A következő érdekes azonosság, permutációk fixpontjainak a kiszámolásánál jött elő:

Lehet adni rá egy egyszerű bizonyítást?
|
|
|



 valós szám esetén számítsuk ki a
valós szám esetén számítsuk ki a 
 0 és f(0):=0, melyeket szokás "lapos" ("flat") függvényeknek is nevezni. Egyszerűen látható, hogy ennek 0-körüli Taylor-sora a konstans 0 függvény, ami nyilván nem állítja elő f-et semmilyen origó körüli intervallumon sem.
0 és f(0):=0, melyeket szokás "lapos" ("flat") függvényeknek is nevezni. Egyszerűen látható, hogy ennek 0-körüli Taylor-sora a konstans 0 függvény, ami nyilván nem állítja elő f-et semmilyen origó körüli intervallumon sem. 
 /17) értékének megkeresését, ami a szabályos 17-szög megszerkesztéséhez kell.
/17) értékének megkeresését, ami a szabályos 17-szög megszerkesztéséhez kell.
 3 esetén an=0. Innen f(x)=ax2+bx alakú lehet, ez pedig mindig jó.
3 esetén an=0. Innen f(x)=ax2+bx alakú lehet, ez pedig mindig jó.