|
|
| [2218] Cckek | 2007-08-08 12:09:35 |
 Gyönyörűszép levezetés, gratula. Azt hiszem, hogy Cesaro-Stolzzal is megy, mármint ha nem csesztem el valahol:)
Első Stolz után 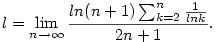
Második Stolz után: 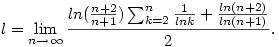
Már csak azt kell felhasználni, hogy 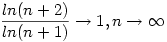 és és 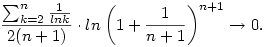
|
| Előzmény: [2217] nadorp, 2007-08-08 00:22:25 |
|
| [2217] nadorp | 2007-08-08 00:22:25 |
 Ennek nem lehet ellenállni :-) ( Remélem jó is lesz a megoldás)
Egy jelölés: Ha {an},{bn} két sorozat, akkor an bn jelölje az asszimptotikus egyenlőséget, tehát hogy bn jelölje az asszimptotikus egyenlőséget, tehát hogy 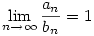 . Felhasználtam a következőket: . Felhasználtam a következőket:
a.) 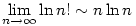
b.) Ha {an},{bn} két pozitív sorozat, és an bn valamint bn valamint 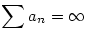 , akkor , akkor 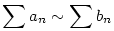
A feladatban szereplő összeg az alábbiak szerint is írható
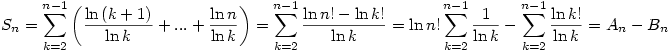
Belátjuk, hogy 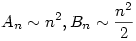 ,innen már következik ,innen már következik 
1.) 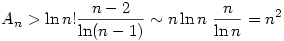
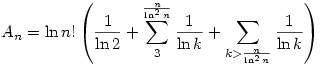
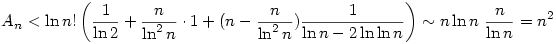
2.) Mivel 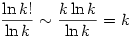 , ezért , ezért
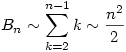
|
| Előzmény: [2213] Lóczi Lajos, 2007-08-07 00:22:27 |
|
|
|
| [2214] Cckek | 2007-08-07 12:23:30 |
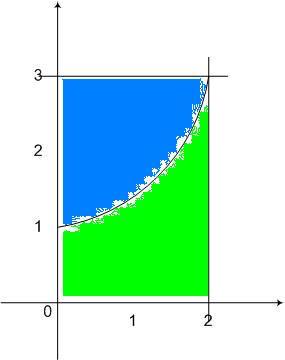
 Tehát az eredmény valóban 6 :) Ha f:[a,b] [c,d] folytonos, növekvő, bijektív függvény akkor [c,d] folytonos, növekvő, bijektív függvény akkor 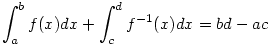 . .
A bizonyítás egyszerű, csak az f(x)=t jelölést kell használni.
Legyen
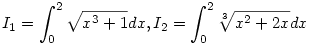 , ,
ekkor I=I1+I2. Jelölés 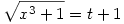 tehát tehát 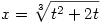 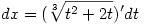 tehát tehát 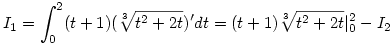
az-az I=6.
Természetesen észrevehető, hogy az előbb kijelentett tételt, egy kicsit más formában használtuk.
Ha f:[a,b] [a+ [a+ ,b+ ,b+ ] folytonos, növekvő, bijektív akkor ] folytonos, növekvő, bijektív akkor
![\int_{a}^{b}\left[f(x)+f^{-1}(x+\alpha )\right] dx=(b-a)(b+a+\alpha )](keplet.cgi?k=6DE24D46B6FB5774)
|
| Előzmény: [2212] Lóczi Lajos, 2007-08-06 20:56:35 |
|
|
| [2212] Lóczi Lajos | 2007-08-06 20:56:35 |
 Az eredmény (borzasztó nagy valószínűséggel) 6. A gép szimbolikus válasza csúnya hipergeometrikus függvényt és gammafüggvényt tartalmaz, de minden numerikus közelítés 6-ot ad.
Lássuk a levezetést és a tanulságokat! :)
|
| Előzmény: [2209] Cckek, 2007-08-04 20:12:02 |
|
| [2211] Csimby | 2007-08-04 23:55:24 |
 Mivel tudjuk, hogy zn is rajta van a komplex egységkörön (hiszen z rajta van), ezért zn szerintem már csak kétféle lehet, amiket írtam, z konjugált vagy -z hiszen ha z=a+bi akkor az y=-b egyenes legfeljebb két pontban metszi a komplex egységkört, -a-bi-ben és a-bi-ben.
|
| Előzmény: [2204] Cckek, 2007-08-04 17:00:39 |
|
|
|
|
| [2207] HoA | 2007-08-04 19:34:06 |
 Ugyanez egy kicsit másképp: n = 3k + 2 esetén zn+z+1=z3k+2+z+1=z2+z+1+z3k+2-z2=(z2+z+1)+z2(z3k-1) és itt a 3. primitív egységgyökök mindkét tagnak gyökei.
|
| Előzmény: [2200] Csimby, 2007-08-04 15:26:15 |
|
|
|
| [2204] Cckek | 2007-08-04 17:00:39 |
 Hogy a képzetes részek egymás ellentettjei ebből nem következik, hogy z és zn egymás konjugáltjai. Probáld inkább a z egységmoduluszú gyök akkor  is gyök utat:) is gyök utat:)
|
| Előzmény: [2202] Csimby, 2007-08-04 16:43:26 |
|
|
| [2202] Csimby | 2007-08-04 16:43:26 |
 Másik biz., amiből kijön a másik irány is: t.f.h. van 1 absz. értékű z megoldás. Ekkor zn is 1 absz. értékű. Mivel z+zn=-1, ezért képzetes részeik egymás ellentettjei, vagyis z és zn egymás konjugáltjai vagy pedig z=-zn. A z=-zn eset kilőve, hiszen akkor z+zn nem -1 hanem 0. Marad az, hogy egymás konjugáltjai, ekkor viszont -1/2 a valós részük (hiszen összegük -1). És máris megkaptuk, hogy z csak 3. primitív egységgyök lehet. Ebből már következik, hogy n=3k+2 hiszen n=3k esetében zn=1, n=3k+1 esetében zn=z és csak n=3k+2 esetben lesz zn egyenlő z konjugáltjával.
|
| Előzmény: [2201] Cckek, 2007-08-04 15:29:15 |
|
|
| [2200] Csimby | 2007-08-04 15:26:15 |
 n=3k+2 esetén zn+z+1=(1+z+z2)(1-z2+z3-z5+...+zn-2) ahol a jobb oldal második tényezőjében váltakozó előjellel szerepelnek z növekvő hatványai és azok maradnak ki amelyekben a kitevő 3k+1 alakú. Mivel 1+z+z2-nek a 3. primitív egységgyökök gyökei és ezek 1 abszolútértékűek, ezért az egyik irány kész van.
|
| Előzmény: [2198] Csimby, 2007-08-04 15:09:43 |
|
|
|
| [2197] Cckek | 2007-08-04 12:53:25 |
 Egy olimpiászfeladat:
Bizonyítsuk be, hogy a zn+z+1=0 egyenletnek akkor és csakis akkor van egységnyi moduluszú komplex gyöke, ha n 3-mal való osztási maradéka 2.
|
|
| [2196] Hajba Károly | 2007-08-02 08:04:16 |
 OK. Akkor teljes szigorral csak n=7-re ismerünk megoldást.
Alacsony n-re szerintem nincs, ha van, akkor az magasabb n-re lesz. Ez minimum n>7, mivel n=7-re vért izzadva leltünk megoldást.
|
| Előzmény: [2194] Csimby, 2007-08-02 00:56:23 |
|



 (3) irracionális" állításról is szól.
(3) irracionális" állításról is szól.

 bn jelölje az asszimptotikus egyenlőséget, tehát hogy
bn jelölje az asszimptotikus egyenlőséget, tehát hogy 
 [c,d] folytonos, növekvő, bijektív függvény akkor
[c,d] folytonos, növekvő, bijektív függvény akkor  [a+
[a+ ,b+
,b+
 zn+zn-1+1=0, a két egyenletet kivonva egymásból kapjuk zn-1-z=0 tehat zn-2=1. De 0=zn+z+1=zn-2.z2+z+1=z2+z+1 tehát z harmadrendű egységgyök, tehát zn-2=z3k=1
zn+zn-1+1=0, a két egyenletet kivonva egymásból kapjuk zn-1-z=0 tehat zn-2=1. De 0=zn+z+1=zn-2.z2+z+1=z2+z+1 tehát z harmadrendű egységgyök, tehát zn-2=z3k=1 2
2 /3 argumentumú komplex számra gondoltam. Tehát
/3 argumentumú komplex számra gondoltam. Tehát  2
2