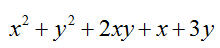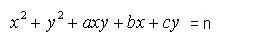|
| [2370] rizsesz | 2007-10-08 20:57:16 |
 (a-y)ad2+(a+z)ad2 = (a-z)ad2+(a+x)ad2 = (a-x)ad2+(a+y)ad2
Ha a szobában vizsgálódunk, akkor feltehető, hogy x, y és z is egyaránt kisebb, mint "a". Ekkor az f(x)=(a-x)ad2 fv. szig. mon. csökkenő, míg g(x)=(a+x)ad2 szig. mon. nő a>0, x>0 miatt. Ha tehát x>=y, akkor (a-z)ad2+(a+x)ad2 = (a-x)ad2+(a+y )ad2 miatt (a-z)ad2<=(a-x)ad2 innen z>=x.
(a-y)ad2+(a+z)ad2 = (a-z)ad2+(a+x)ad2 is igaz viszont, és ebből teljesen hasonlóan y>=z, ami az előzőek miatt azt jelenti, hogy y>=z>=x>=y, ami azt jelenti, hogy csak az lehetséges, hogy a 3 szám egyenlő.
(valamiért nem megy semmi a teX-kel kapcsolatban :(). Az ad a hatvány-jel.
|
| Előzmény: [2353] SmallPotato, 2007-10-02 14:29:53 |
|
| [2369] epsilon | 2007-10-07 13:31:32 |
 Kedves Róbert Gida! Valóban szórakozom, de nem mással, mint éppen ez utóbbi feladatnak egy másik megoldásával és az általánosításával. Ha észrevetted, a 2359-es hozzászólás ezt a feladatot általánosítja, éppen ezért, ott az n nem csak páros. Tehát, ha ez utóbbi annak a sajátos esete, akkor érthető, hogy sajátos számok, feltételek állnak ez esetben.
|
| Előzmény: [2367] Róbert Gida, 2007-10-07 13:14:52 |
|
|
| [2367] Róbert Gida | 2007-10-07 13:14:52 |
 Most szórakozol, vagy mi? Egyetlen szóval sem írtad, hogy páros nemnegatív számokra kérted csak az előállítást. Egyébként, ahogy megoldottam úgy is teljesen értelmes feladat volt. Gondolatolvasó pedig (még) nem vagyok.
Itt az új feladat megoldása, bár lövésem sincs, hogy most ezt akarod-e megoldani: x2+y2+2*x*y+x+3*y=2*n-nek keressük nemnegatív egész megoldását minden n 0-ra. x-re rendezve az egyenletet: 0-ra. x-re rendezve az egyenletet:
x2+(2*y+1)*x+(y2+3*y-2*n)=0
Ennek a megoldásai:
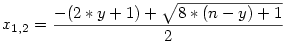
Legyen a az az egyértelműen meghatározott nemnegatív egész szám, amelyre teljesül, hogy (2*a+1)2 8*n+1<(2*a+3)2. Ekkor, mivel minden páratlan négyzetszám 8k+1 alakú, ezért van olyan nemnegatív y, amelyre: 8*(n-y)+1=(2*a+1)2, innen 8*n+1<(2*a+3)2. Ekkor, mivel minden páratlan négyzetszám 8k+1 alakú, ezért van olyan nemnegatív y, amelyre: 8*(n-y)+1=(2*a+1)2, innen 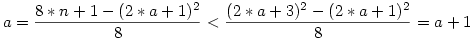 azaz y azaz y a, ezért a, ezért  és persze egész, ami kellett, így valóban minden nemnegatív páros egész előáll nemnegatív x,y segítségével, a bizonyításból egyébként az is kiderül,némi munkával, hogy az előállítás ráadásul egyértelmű. és persze egész, ami kellett, így valóban minden nemnegatív páros egész előáll nemnegatív x,y segítségével, a bizonyításból egyébként az is kiderül,némi munkával, hogy az előállítás ráadásul egyértelmű.
|
| Előzmény: [2365] epsilon, 2007-10-07 09:37:55 |
|
| [2366] epsilon | 2007-10-07 10:07:22 |
 Elfelejtettem pontosítani: x és y nemnegatív egészek lehetnek!
|
|
|
|
|
|
| [2361] nadorp | 2007-10-06 18:19:25 |
 Ha x2+y2=8n+10, akkor x és y azonos paritású, tehát, 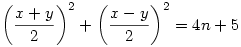 miatt 4n+5 is két egész szám négyzetösszege. Ismert, hogy egy egész szám akkor lehet két egész négyzetösszege, ha a prímtényezős felbontásában minden 4k-1 alakú prím páros kitevőn szerepel. Ebből következik, hogy például a miatt 4n+5 is két egész szám négyzetösszege. Ismert, hogy egy egész szám akkor lehet két egész négyzetösszege, ha a prímtényezős felbontásában minden 4k-1 alakú prím páros kitevőn szerepel. Ebből következik, hogy például a
3.7(2x-1)2=21(2x-1)2
alakú számok nem állnak elő két egész négyzetösszegeként, tehát a 42(2x-1)2 alakúak sem, pedg 8n+10 alakúak
|
| Előzmény: [2357] epsilon, 2007-10-06 08:57:35 |
|
| [2360] Róbert Gida | 2007-10-06 16:47:17 |
 x=0,y=0 esetén p(x,y)=0
x>0 vagy y>0-ra p(x,y)>1 Azaz már az 1 sem áll elő. A helyzet még ennél is rosszabb, ugyanis végtelen sok pozitív egész szám nem áll elő, ezt a megoldások számának triviális felső becslésável lehet belátni, n=K2-ig tekintve a megoldásokat.
|
| Előzmény: [2359] epsilon, 2007-10-06 13:40:30 |
|
| [2359] epsilon | 2007-10-06 13:40:30 |
 Köszi, egy átalakításnál elnéztem a feladatot ami erre vezetett. Valójában az érdekelne, hogy milyen a, b, c, pozitív egész számok esetén van nemnegatív egészekből álló megoldása az alábbi egyenletnek, minden n pozitív egész számra. Szakirodalom a neten, az is érdekelne! Előre is kösz!
|
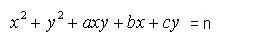 |
| Előzmény: [2357] epsilon, 2007-10-06 08:57:35 |
|
|
| [2357] epsilon | 2007-10-06 08:57:35 |
 Helló! A következő kérdésre nem találok azonnali választ :-( "Ihazoljuk, hogy minden nemnegatív n egész szám esetén 8n+10 felírható két páratlan egész szám négyzetösszegeként!" Bármilyen tippet előre is köszönök! Üdv: epsilon
|
|
|
| [2354] rizsesz | 2007-10-02 15:18:11 |
 Ezekből az egyenletekből páronként 2x=y+z, 2y=x+z, 2z=x+y, és ezekből x=y=z könnyen jön, ami valóban az említett egyenes. nem :D?
|
|
| [2353] SmallPotato | 2007-10-02 14:29:53 |
 "Egy kocka 3 kitérő élétől egyenlő távolságra levő pontok halmaza micsoda?"
Erős meggyőződésem szerint a kérdéses mértani hely egy egyenes. Konkrétan az az egyenes, amely tartalmazza a kockának azon (egyetlen) testátlóját, amely mindhárom jelzett kitérő élhez képest kitérő.
Bizonyítani sajnos nem tudom. :-(
Eljutottam egy ilyen, a kérdéses mértani hely (x,y,z) pontjait leíró egyenletrendszerhez (a kocka élhossza 2a, élei a koordinátatengelyekkel párhuzamosak, középpontja az origóban):
(a-y)2+(a+z)2 = (a-z)2+(a+x)2 = (a-x)2+(a+y)2
Ennek a jelzett egyenes pontjai valóban eleget tesznek - de elvben talán más pontok is? Nem tudom.
|
| Előzmény: [2255] rizsesz, 2007-09-02 20:52:05 |
|
|
| [2351] nadorp | 2007-10-01 09:45:33 |
 Köszönöm a hozzászólásokat. Én Lóczi Lajoshoz hasonlóan csináltam. A sin(x+15o)=sin18o egyenletnek a 3o és 147o a megoldása. Ez a sin xcos15o+cos xsin15o=sin18o egyenletre vezet. Ebből sin x-re egy másodfokú egyenletet kapunk, aminek a kisebbik gyöke sin3o
|
|
|
| [2349] SmallPotato | 2007-09-30 23:48:36 |
 A 18 fokos szög szögfüggvényeinek megállapításához (a készen kapható ötleteken kívül, persze) a 72-72-36 fokos szögekkel bíró egyenlőszárú háromszöget javaslom; ennek oldalarányai (ha ugyan fejből nem ismertek :-) ) annak felismerésével határozhatók meg, hogy az egyik 72 fokos szög felezője a szemközti oldalból saját magával azonos hosszúságú szakaszt metsz ki, a másik metszék pedig egy újonnan keletkezett kisebb, szintén 72-72-36 fokos háromszög legkisebb oldala.
|
| Előzmény: [2348] SmallPotato, 2007-09-30 23:40:47 |
|
|
| [2347] Lóczi Lajos | 2007-09-30 23:13:51 |
 [Nyilván 3=18-15, és a félszögképlet miatt csak a 18 fok szinuszán kell kicsit gondolkodni, de a példatárakban (pl. Geom. feladatgyűjtemény) az aranymetszésnél ez utóbbi szög szinusza is ki van számolva (Mathematica alatt: Sin[3 Degree] // FunctionExpand, weben (még egy felezésre szükség van): http://functions.wolfram.com/ElementaryFunctions/Sin/03/02/).]
|
| Előzmény: [2344] nadorp, 2007-09-30 20:05:12 |
|
|




 0-ra. x-re rendezve az egyenletet:
0-ra. x-re rendezve az egyenletet:  8*n+1<(2*a+3)2. Ekkor, mivel minden páratlan négyzetszám 8k+1 alakú, ezért van olyan nemnegatív y, amelyre: 8*(n-y)+1=(2*a+1)2, innen
8*n+1<(2*a+3)2. Ekkor, mivel minden páratlan négyzetszám 8k+1 alakú, ezért van olyan nemnegatív y, amelyre: 8*(n-y)+1=(2*a+1)2, innen