|
| [2395] Gyöngyő | 2007-10-21 11:58:43 |
 mátrix szorzásról van szó.
üdv.Gyöngyő
|
|
|
|
|
| [2391] Gyöngyő | 2007-10-20 15:49:02 |
 Sziasztok!
Nekem is lenne egy kérdésem egy másik feladattal kapcsán:
Adva van P és Q hermetikus idempotens mátrix,ugyanaz a dimenziójuk és a rangjuk is. Bizonyítsuk be,hogy ha P*Q*P=P,akkor P=Q.
Üdv: Gyöngyő
|
|
| [2390] HoA | 2007-10-19 16:42:01 |
 A feladatban szereplő egyesszámú kérdés: "Milyen színű kör marad végül a táblán?" és a több kört megengedő válasz: "páratlan fehér kör marad meg" felveti a feladat folytatásának lehetőségét:
a) 2k+1 , 2l, 2m+1 különböző színű körből indulva biztos-e, hogy végül 1 db. kör marad?
Ha nem, akkor
b) 2k+1 , 2l, 2m+1 különböző színű körből indulva van-e olyan stratégia, mellyel végül 1 db. kör marad?
|
| Előzmény: [2388] Hajba Károly, 2007-10-18 23:52:58 |
|
| [2389] Cckek | 2007-10-19 07:30:31 |
 Igen, a bizonyítás tökéletes. A gyerekek számára viszont elég nehezeknek tűnnek ezek az invariánsok elvére épülő feladatok. Itt van még egy:
Adott a síkban az A(x,y) kordinátájú pont. A következő kordinátájú pontokba léphetünk:
(x+1,y+1),(x-1,y+1),(x-1,y-1),(x+1,y-1).
Bizonyítsuk be, hogy az origóból nem juthatunk el a (2007,2008) kordinátájú pontba.
|
| Előzmény: [2388] Hajba Károly, 2007-10-18 23:52:58 |
|
| [2388] Hajba Károly | 2007-10-18 23:52:58 |
 A művelet végzése során mindhárom halmaz és az összhalmaz paritása is az ellenkezőjére fordul. Azaz mindig lesz egy halmaz, melynek a paritása mindig megegyezik az összhalmaz paritásával. Ez akkor sem változik, mikor a másik két halmaz már üres. Ez akkor működik így, ha a három halmaz paritásaiban van különböző.
Jelen példánál az összhalmaz paritása páros, ezért páratlan fehér kör marad meg.
Valóban érdekes kis feladat.
|
| Előzmény: [2387] Cckek, 2007-10-18 21:48:34 |
|
| [2387] Cckek | 2007-10-18 21:48:34 |
 Egy számotokra, tisztelt fórumozók, egyszerű, ugyanakkor nagyon kedves kis feladat:
A táblára fel van rajzolva 999 piros, 1000 fehér és 1001 zöld kör. A következő műveletet végezzük: letörlünk két különböző színű kört és helyette rajzolunk egy olyat amilyent nem töröltünk. Milyen színű kör marad végül a táblán?
|
|
| [2386] Csimby | 2007-10-15 00:47:27 |
 Köszi! Nekem is majdnem ez jött ki, csak a vége: 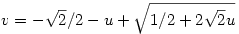 Ami azért tűnik jobbnak, mert u=0-ra v=0 jön ki. Én úgy csináltam, hogy (x,x) pontból merőlegest állítottam x=y-ra, ennek és Ami azért tűnik jobbnak, mert u=0-ra v=0 jön ki. Én úgy csináltam, hogy (x,x) pontból merőlegest állítottam x=y-ra, ennek és 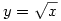 -nek a metszéspontja legyen (y,y2). És akkor a fv. amit keresünk, az |(x,x)|-hez rendeli (y,y2) és (x,x) távolságát. De kb. ugyanilyen gyorsan kijön, mert lehet találni egy egyenlőszárú derékszögű háromszöget. Ez lehet hogy elsőre csúnyának tűnik, de hamar kijön ezzel is. -nek a metszéspontja legyen (y,y2). És akkor a fv. amit keresünk, az |(x,x)|-hez rendeli (y,y2) és (x,x) távolságát. De kb. ugyanilyen gyorsan kijön, mert lehet találni egy egyenlőszárú derékszögű háromszöget. Ez lehet hogy elsőre csúnyának tűnik, de hamar kijön ezzel is.
|
| Előzmény: [2385] jonas, 2007-10-14 23:26:45 |
|
| [2385] jonas | 2007-10-14 23:26:45 |
 Én is csak kiszámolni tudnám (noha nem egyértelmű, hogy a legegyszerűbb kiszámolni).
Az eredeti koordinátarendszerben a grafikon azon (x,y) pontok halmaza, amire y2=x. A forgatás az (u,v) pontot az 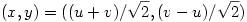 pontból kapja. Ebből pontból kapja. Ebből 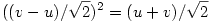 , amiből , amiből 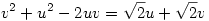 , azaz , azaz 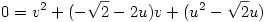 . Ez másodfokú, megoldva (nyilván a nagyobbik megoldás kell) . Ez másodfokú, megoldva (nyilván a nagyobbik megoldás kell) 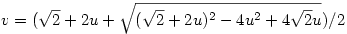 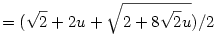 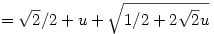
Azt előre tudjuk, hogy a megoldás egyszerű alakú lesz, mert egy kúpszelet elforgatva is kúpszelet.
|
| Előzmény: [2383] Csimby, 2007-10-14 22:42:52 |
|
| [2384] Csimby | 2007-10-14 22:45:28 |
 Hivatkozni tényleg jobb úgy. De azért az nem rossz ha látszik egy hozzászóláson hogy ez most új feladat, vagy csak a 20.hozzászólás valamihez. A könyvekben is vannak fejezetek, noha az oldalszám alapján egyszerűbben lehet hívatkozni.
|
| Előzmény: [2381] jonas, 2007-10-14 16:36:28 |
|
| [2383] Csimby | 2007-10-14 22:42:52 |
 (a 126.feladatra gondolsz? ;-))
A megoldását mondjuk nem találtam meg. A sajátomnak tudom, csak arra lennék kíváncsi hogy lehet-e valahogy egyszerűbben, mert én mint geometria feladatot "kiszámoltam".
|
| Előzmény: [2382] Lóczi Lajos, 2007-10-14 20:28:59 |
|
|
| [2381] jonas | 2007-10-14 16:36:28 |
 (Szerintem egyébként a hozzászólás sorszáma alapján könnyebb hivatkozni. Adott sorszámú hozzászólást könnyebb megkeresni, mint adott sorszámú feladatot, különösen, ha nem nagyon sűrűn vannak feladatok a topikban. Ráadásul így nem fordulhat elő, hogy valaki tévedésből rossz sorszámot ad, vagy hogy ugyanazzal a sorszámmal egyszerre két ember tűz ki feladatot. Ennek azonban nincs túl nagy jelentősége, a feladat sorszámozás is tökéletesen jó módszer.)
|
|
| [2380] Csimby | 2007-10-14 12:54:23 |
 329. feladat (Nyilván nem a 329.-edik, de ez volt az az utolsó sorszám amit találtam, 10 oldallal korábban és azt is én írtam... Szerintem nem olyan megerőltető odaírni hogy hanyadik feladatról van szó, viszont úgy sokkal egyszerűbb hivatkozi rá)
Az 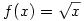 függvénygörbét forgassuk el az origó körül 45°-kal az óramutató járásával megegyező irányba. Mi az így kapott görbe egyenlete? függvénygörbét forgassuk el az origó körül 45°-kal az óramutató járásával megegyező irányba. Mi az így kapott görbe egyenlete?
|
|
|
|
|
|
|
|
|
| [2372] SmallPotato | 2007-10-08 21:44:00 |
 Értem, köszönöm!
(Az efféle "körszimmetrikus" egyenletrendszerekkel többnyire elakadok: érzem én, hogy ha pontosan egyformán fordulnak elő a változók, akkor egyenlőknek kell lenniük - csakhát az érzés nem bizonyítás, ugye ... :-)) )
|
| Előzmény: [2370] rizsesz, 2007-10-08 20:57:16 |
|










 N függvényt, melyekre:
N függvényt, melyekre:  m,n
m,n N
N