| [2521] Lóczi Lajos | 2007-12-28 21:18:43 |
 Nem értem ezt. Kérlek, mondd ki, mi az állításod és mit bizonyítasz.
"Innen generalizálással adódik az állitás." Ez mit jelent és melyik állítás?
"P=PP=PPP implikálja TQ=TTQ implikáció ugyanaz, mint T=TQT." Ez nem magyar mondat. Kérlek, tisztázd.
Mit jelölsz felső vesszővel?
Stb.
|
| Előzmény: [2519] hobbymatekos, 2007-12-28 00:35:05 |
|
|
| [2519] hobbymatekos | 2007-12-28 00:35:05 |
 Ez már hermitikus és idempotens is. És pozitiv szemidefinit. Diagonizálható. Egy diagonál mátrix pedig triviálisan hermitikus és idempotens, ha elemei valósak (csak ekkor hermitikus definició szerint). Legyen M mxn mátrix, rangja n. És oszlopai ortonormáltak, P=MM' hermitikus,ha főátlóbeli elemei valósak, továbbá ortonormáltság miatt M'M=I , nxn es identitás. Létezik U unitér mátrix, T=U'PU. Mivel P hermitikus, T is az. PP=P implikálja TT=T, hiszen minden diagonális elem 1 vagy nulla és a rang ugyanannyi marad, azaz T n db 1 est és m-n db nullát tartalmaz főátlójában. Azaz P=UTU'=UTTU=UT'U'UT'U=MM' és M olyan mátrix, hogy n oszlopa U beli. Innen generalizálással adódik az állitás. Q rangja ugyanannyi mint P nek, valamint hermitikus idempotens.
P=PP=PPP implikálja TQ=TTQ implikáció ugyanaz, mint T=TQT.
|
| Előzmény: [2518] Cckek, 2007-12-26 14:17:40 |
|
|
|
| [2516] Cckek | 2007-12-26 13:08:46 |
 Hmm, szerinted tehát csak O illetve I idempotens? Amugy az idempotencia ebben az esetben a sor/oszlop mátrixszorzásra vonatkozik, s gondolom ott követted el a hibát hogy így ültetted át az értelmezést: x (G,*) idempotens, ha x*x=x, most pedig a *-ot sorra a + illetve . műveletekkel helyetesítetted. Keress olyan négyzetes másodrendű mátrixokat melyeknek nyoma 1 determinánsa 0. Ezek mind idempotensek lesznek:D (G,*) idempotens, ha x*x=x, most pedig a *-ot sorra a + illetve . műveletekkel helyetesítetted. Keress olyan négyzetes másodrendű mátrixokat melyeknek nyoma 1 determinánsa 0. Ezek mind idempotensek lesznek:D
pl: 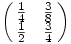
|
| Előzmény: [2515] hobbymatekos, 2007-12-26 12:43:15 |
|
| [2515] hobbymatekos | 2007-12-26 12:43:15 |
 A nullelem idempotens az összeadás és szorzás binér műveletre. A nullelemtől különböző elemek közül csak az egységelem idempotens és csak a szorzásra nézve. Mivel az állitás csak szorzást tartalmaz, ezért 0 vagy egységelemre teljesülhet az idempotencia. Az állitás a hermitikus mátrixok körében csak a valós P=Q=0 vagy P=Q=I mátrixokra igaz. De nem igaz, hogy csak P=Q-ra igaz. Ha Q=I akkor tetszőleges P re igaz. Ha P=0 akkor tetszőleges Q ra igaz. Q=0 ra nem igaz.
|
| Előzmény: [2513] Cckek, 2007-12-26 01:02:06 |
|
|
|
|
|
|
| [2509] hobbymatekos | 2007-12-25 23:25:13 |
 Def.: A idempotens ha A+A=AA=A.
A feltétel szerint P, Q hermitikus és idempotens volt. P=QP egyenlőség tetszőleges nem elfajuló (detP vagy detQ nem nulla) mátrixokra pl: Q=I lenne, de I nem idempotens.
|
| Előzmény: [2508] Lóczi Lajos, 2007-12-25 21:42:39 |
|
| [2508] Lóczi Lajos | 2007-12-25 21:42:39 |
 Nem egészen értem, mit írsz.
"Def.: A idempotens ha A+A=AA=A A feltétel szerint P, Q hermitikus és idempotens volt P=QP egyenlőség tetszőleges nem elfajuló (detP vagy detQ nem nulla) mátrixokra pl: Q=I lenne, de I nem idempotens."
Át tudnád ezt fogalmazni magyarosabbra? Összefolynak a részek. Amúgy miért veszed bele az idempotens definíciójába az összeget?
|
| Előzmény: [2505] hobbymatekos, 2007-12-25 17:05:24 |
|
|
|
| [2505] hobbymatekos | 2007-12-25 17:05:24 |
 Egyelőre csak a következőt sikerült igazolnom: P=PQ=QP Ez segédtételből következik: Ha P és Q hermitikus, akkor PQ=QP(kommutativitás) továbbá P ill. Q idempotens (a feltételek szerint) Def.: A idempotens ha A+A=AA=A A feltétel szerint P, Q hermitikus és idempotens volt P=QP egyenlőség tetszőleges nem elfajuló (detP vagy detQ nem nulla) mátrixokra pl: Q=I lenne, de I nem idempotens. Hermitikus, idempotens mátrixokra Q=P.
|
| Előzmény: [2399] Lóczi Lajos, 2007-10-22 12:32:28 |
|
| [2504] Cckek | 2007-12-24 16:57:02 |
 Kellemes, boldog és békés Karácsonyt minden tisztelt forumozónak. ...és a piával csak Lebesque mértékkel:D
|
|
| [2503] Lóczi Lajos | 2007-12-24 02:16:45 |
 Igen, a feladat érdekessége abban van, hogy indukcióval közvetlenül nem jön ki, viszont egy nála erősebb állítás igen: ha a jobb oldalra  -et írunk, az indukció már végigmegy. -et írunk, az indukció már végigmegy.
|
| Előzmény: [2501] Csimby, 2007-12-24 01:26:49 |
|
| [2502] rizsesz | 2007-12-24 01:30:03 |
 pedig van indukciós, csak sajna nem saját :( úgyhogy nem dobom be a közösbe (viszon Csimby megoldása szép!).
más kérdés: az első 2n pozitív egész számból kiválasztunk k. mekkora k értéke, ha tudjuk, hogy k-ra igaz, hogy van a k szám között 3 olyan, amelyek közül az egyik a másik kettő összege, továbbá az is igaz, hogy ez már k-1 esetén nem teljesül?
|
| Előzmény: [2501] Csimby, 2007-12-24 01:26:49 |
|
|
|
|
|
| [2497] Gyöngyő | 2007-12-22 11:08:52 |
 Sziasztok!
Segítséget szeretnék kérni! Az lenne a kérdésem,hogy hol találok olyan feladatokat,amiben a teljes indukció kicsit furcsa modon kerül elő vagy nem teljesen követi a megszokott utat!
Köszönettel: Zsolt
|
|





 (G,*) idempotens, ha x*x=x, most pedig a *-ot sorra a + illetve . műveletekkel helyetesítetted. Keress olyan négyzetes másodrendű mátrixokat melyeknek nyoma 1 determinánsa 0. Ezek mind idempotensek lesznek:D
(G,*) idempotens, ha x*x=x, most pedig a *-ot sorra a + illetve . műveletekkel helyetesítetted. Keress olyan négyzetes másodrendű mátrixokat melyeknek nyoma 1 determinánsa 0. Ezek mind idempotensek lesznek:D  A=A-A=O(n) az-az az "idempotencia feltételed" csak a nullmátrixra teljesül.
A=A-A=O(n) az-az az "idempotencia feltételed" csak a nullmátrixra teljesül.
