|
|
| [2973] Lóczi Lajos | 2009-06-17 12:16:38 |
 Itt egy másik rokon klasszikus feladat.
Egy falhoz támasztott létra az ábrán látható módon lecsúszik. (A létra két vége tehát mindig érinti a falat, illetve a padlót.) Írjuk fel az így kialakult burkológörbét.
|
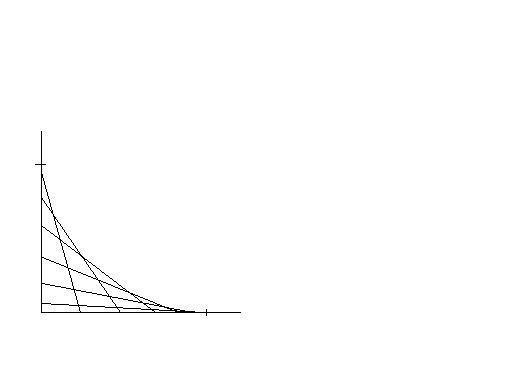 |
|
| [2972] Alma | 2009-06-17 03:19:46 |
 A feladathoz annyit fűznék hozzá, hogy ez fizikus körökben egy nagyon ismert feladat (illetve ennek a háromszöges verziója, mely lényegében ugyanez). Középiskolai módszerekkel jól tárgyalható, nem kellenek komplex számok sem hozzá. A feladaton keresztül be lehet vezetni a polárkoordinátákat, mert messze célravezetőbb használatuk ebben az esetben, mint a Descartes-koordinátáké. Polárkoordinátákban gondolkodva lényegében 3-4 sor a feladat megoldása.
|
| Előzmény: [2961] Lóczi Lajos, 2009-06-16 00:07:09 |
|
|
| [2970] Tibixe | 2009-06-16 22:23:33 |
 Vegyük fel az ábrát a komplex számsíkon, úgy hogy a négyzet középpontja a 0 pont legyen.
Egy kiválasztott teknős pályáját írja le az F(t) függvény, ahol t egy valós paraméter (pl. idő).
Szimmetriaokokból a következő teknős helye a kiválasztott teknős helye 90o-kal elforgatva, azaz i-vel szorozva.
Fk(t)=iF(t)
A teknős sebességének iránya mindig a következő felé mutat, a nagysága a feladat szempontjából lényegtelen, most válasszuk meg kényelmesen.
F'(t)=Fk(t)-F(t)
azaz
F'(t)=iF(t)-F(t)
F'(t)=(i-1)F(t)
Ez egy pofonegyszerű differenciálegyenlet, a megoldásai pedig:
F(t)= e(i-1)t e(i-1)t
alakúak, ahol  tetszőleges komplex szám. tetszőleges komplex szám.
Ha például azt akarjuk, hogy a kiválasztott teknős t=0-nál az (1;1) pontban legyen, akkor
 =1+i =1+i
kell nekünk.
Ezzel nem csak négyzetre, hanem más szabályos n-sokszögekre is fel lehet írni a pályát:
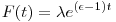
ahol  egy megfelelő n-edik egységgyök. egy megfelelő n-edik egységgyök.
F(t) alakjából látszik, hogy a megoldás logaritmikus spirál lesz, amely az origóba tart.
|
| Előzmény: [2969] HoA, 2009-06-16 21:21:39 |
|
| [2969] HoA | 2009-06-16 21:21:39 |
 Szimmetria okokból a négy pont mindig egy négyzet csúcsaiban helyezkedik el és e négyzetek középpontja közös ( O ) . A pályák érintője kezdetben 45oos szöget zár be az O -ból a görbe pontjába mutató vektorral. A pontnégyes bármelyik későbbi helyzetét is tekinthetjük a további mozgás kiindulópontjának, így ez a tulajdonság a pályák további pontjaira is igaz. A négy pálya tehát négy olyan görbe, melynek minden P pontjára az OP helyvektor 45o -os szöget zár be a P-beli érintővel. A logaritmikus spirálok egyenletének felírását meghagyom a következő hozzászólónak.
|
| Előzmény: [2961] Lóczi Lajos, 2009-06-16 00:07:09 |
|
|
|
|
| [2965] nadorp | 2009-06-16 12:14:11 |
 Ezt a kérdést most nem értem. A rekurzióból látszik, hogy a sorozatot az első elem egyértelműen meghatározza, másrészt "adja magát", hogy generátor függvényt használjunk és hogy ennek a négyzetét kell vizsgálni ( "látszik", hogy a rekurzió két polinom szorzatában az n+1-ed fokú tag együtthatóját tartalmazza).
|
| Előzmény: [2962] Lóczi Lajos, 2009-06-16 00:08:23 |
|
| [2964] sakkmath | 2009-06-16 11:04:40 |
 Csatlakozom rizseszhez annyiban, hogy érdemes pontosítani a szöveget a triviális esetek kiküszöbölése céljából.
Közölni kellene azt, hogy a "szomszéd" a csúcsok mely körüljárási iránya szerint értendő. Ha a rajz a feladat eredeti szövegéhez készült, akkor (a mi nézőpontunkból) az óramutató járásával ellentétes irányt kell még megadni.
|
| Előzmény: [2961] Lóczi Lajos, 2009-06-16 00:07:09 |
|
|
|
| [2961] Lóczi Lajos | 2009-06-16 00:07:09 |
 Egy négyzet 4 sarkából a szomszédja felé egyenletes sebességgel egyszerre elindul 4 pont, és e pontok mindvégig egymást üldözik. Írjuk fel a mozgások pályáit.
|
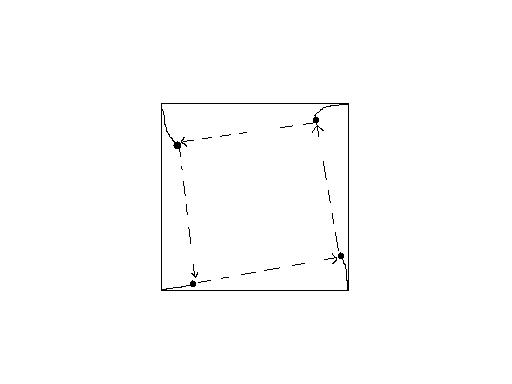 |
|
|
| [2959] nadorp | 2009-06-12 11:31:59 |
 Ha van elemibb - nem analízist használó - akkor érdekel. Egyébként itt egy analitikus vázlat.
Legyen 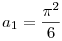 és n és n 2 esetén 2 esetén
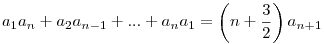
Azt kell bizonyítani, hogy an= (2n) (2n)
Könnyű látni indukcióval, hogy an a1n, tehát az a1n, tehát az
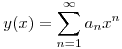
sorfejtés biztos értelmes a 0 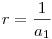 sugarú környezetében. sugarú környezetében.
A rekurziót felhasználva kapjuk, hogy
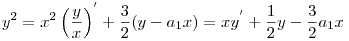
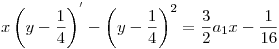
Legyen most
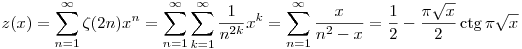
( A fenti utolsó egyenlőség a cotangens függvény parciális törtekre bontásából adódik). Ellenőrizhető, hogy a z(x) függvény kielégíti a fenti diffenciálegyenletet és 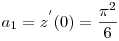 is teljesül, ezért a bizonyítás kész. is teljesül, ezért a bizonyítás kész.
|
| Előzmény: [2954] Gyöngyő, 2009-06-04 23:29:11 |
|
| [2958] S.Ákos | 2009-06-10 16:07:48 |
 Mely p prímekre lesz 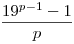 négyzetszám? négyzetszám?
|
|
| [2957] Gyöngyő | 2009-06-08 20:06:27 |
 Sziasztok!
Ha valakit érdekel a megoldás,akkor szóljon,és elküldöm mailbe!
|
|
| [2954] Gyöngyő | 2009-06-04 23:29:11 |
 Sziasztok! Itt egy érdekes feladat:
Legyen  a Riemann-féle Zeta-függvényt. a Riemann-féle Zeta-függvényt.
Bizonyítsd be, hogy minden n 2-re 2-re
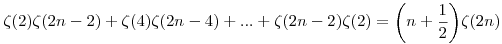
|
|
|
|
|
| [2950] jonas | 2009-05-18 19:00:39 |
 Várj, ezt részletezem. Gimp-ben először megnyitod a képfájlt úgy, hogy letöltöd, majd a File menüből az Open parancsot választod, majd kiválasztod a letöltött képfájlt. Kiválasztod a Select by Color tool-t, és a Tool Options dialogban a Threshold csúszkát nullára állítod. Utána rákattintassz a képre valahol, ezzel kijelölted a képben az egyforma színű pixeleket. Ezután a színváltó melletti kis gombbal visszaállítod az aktuális előtérszínt feketére, a háttérszínt fehérre, majd a képen az Edit menüből lefuttatod a Fill with BG Color parancsot, ami fehérre színezi a kijelölést. Végül a Select menüből kiválasztod a None opciót, hogy a kijelölés határát mutató esetleges keret ne zavarjon.
|
| Előzmény: [2949] jonas, 2009-05-18 18:36:33 |
|
| [2949] jonas | 2009-05-18 18:36:33 |
 Megnyitod egy képszerkesztőben, választassz egy szimpatikus pontot a képen, kijelölöd az összes olyan pontot, ami pontosan ugyanolyan színű, mint az a pont, és ezeket átszínezed fehérre.
|
| Előzmény: [2947] HoA, 2009-05-18 18:26:57 |
|



 x0). A derivált és második derivált vizsgálatából következik, hogy
x0). A derivált és második derivált vizsgálatából következik, hogy 




 e(i-1)t
e(i-1)t egy megfelelő n-edik egységgyök.
egy megfelelő n-edik egységgyök. 


 2 esetén
2 esetén  (2n)
(2n) 


