|
| [3153] R.R King | 2010-01-08 16:04:51 |
 Üdv. neten nézegettem hatványsorokat. Az arcsinx hatványsorával kellene valamit kezdeni, mert eléggé hasonlít az általad megadottra..Csak egy ötlet, lehet nem így kell nekifogni.
|
| Előzmény: [3149] Cokee, 2010-01-07 15:20:42 |
|
|
|
|
| [3149] Cokee | 2010-01-07 15:20:42 |
 Számítsuk ki a következő összeget:
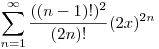
ahol |x|<1
Üdv.: Cokee
|
|
|
| [3147] Lóczi Lajos | 2010-01-05 01:35:52 |
 Ezek szerint az alábbi általánosabb állítás is igaz:
ha f az egész számegyenesen értelmezett deriválható függvény és létezik az
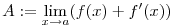
határérték, akkor létezik a
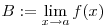
határérték is és A=B.
1. A fentiekben tehát a és A tetszőleges véges szám lehet, vagy a két végtelen bármelyike, egymástól függetlenül.
2. Persze ebben az általánosabb szituációban 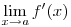 értékéről általában nem tudunk semmit mondani. értékéről általában nem tudunk semmit mondani.
|
| Előzmény: [3146] Cogito, 2010-01-04 11:13:53 |
|
| [3146] Cogito | 2010-01-04 11:13:53 |
 A 4. kérdés tényleg kipipálva (és pofonegyszerűen). :)) A lim f '=0 esettel kapcsolatban olyan függvényeket is vizsgáltam, amelyekről csak később derült ki, hogy szétfeszítik a 4. feladat feltételeit és már csak egy újabb, 5. feladatba férnek bele ... .
[3145)-ös kérdésedre holnap tudok egész pontosan válaszolni. Most nincs nálam a könyv, de arra emlékszem, hogy a tételidézetem végén, a (...) helyen Rudin hivatkozik egy korábbi fejezetre, az pedig egy mégkorábbira. Így magát az - önmagában is terjedelmes - bizonyítást érdemes ezekkel mind összeolvasni. Holnap megpróbálom összeollózni és beszkennelni mindezt, s e-mail-ben elküldöm (a szerzői jogok ugyebár ...). Azt ellenőriztem, hogy e hivatkozásokkal együtt is érvényes a tétel a feladatunkra.
|
| Előzmény: [3143] Lóczi Lajos, 2010-01-03 01:24:47 |
|
|
| [3144] Ló Béla | 2010-01-03 12:43:02 |
 Adott n db racionális szám. Be kellene öket m db csoportba osztani úgy, hogy az egy csoporton belül lévö számok összegének legnagyobbika a lehetö legkisebb legyen. Hogy helyezzünk el egy n+1-ik elemet, ha n elemet már sikerült besorolnunk ?
|
|
| [3143] Lóczi Lajos | 2010-01-03 01:24:47 |
 Nagyon érdekes, amit mondasz. Valaki az interneten idézi a Rudin-féle bizonyítást: szerintem az teljesen rendben van. Ezek szerint a tankönyvek mindig csak egy speciális esetet bizonyítanak be akkor, amikor a nevező a végtelenbe tart!
(Kíváncsi lennék, mielőtt a könyvtárban megnézem, hogy pl. a Császár-féle könyv mit mond erről a kérdésről.)
A feladat 1-3. kérdéseit tehát a Rudin-féle általánosabb L'Hospital-szabály megoldja. Az én bizonyításom az A=B állításra pedig szinte szóról szóra az volt, amit Rudin is csinál (persze ő általánosan, én pedig csak az u(x)=f(x) exp(x), v(x)=exp(x) esetben bizonyítottam); nem biztos, hogy könnyű lenne találni olyan bizonyítást, ami nem "L'Hospital-szerű".
Nem értem, hogy a 4. kérdésen miért gondolkozol még :), jonas a [3130]-ban rámutatott, hogy a 4. kérdés igaz volta következik a 3. kérdés igazságából.
|
| Előzmény: [3142] Cogito, 2010-01-01 17:57:48 |
|
|
| [3141] Lóczi Lajos | 2009-12-29 23:39:34 |
 Hármas ciklusra is van példa bőven: az első százezer pozitív egészt, mint kezdőértéket addig iterálva, amíg a C függvény ciklusba nem kerül, azt tapasztaljuk, hogy a 100000 kezdőérték közül 11467 db végződik előbb-utóbb fixpontban, 65638 db 2-es ciklusban, 22895 db pedig 3-as ciklusban.
A legkisebb kezdőérték, amelyből 3-as ciklusban végződik a rekurzió, az n=50.
Az tehát ebből a sejtés, hogy a 4-es és magasabb elemszámú ciklusok elég ritkák (ha egyáltalán vannak??).
|
| Előzmény: [3117] Lóczi Lajos, 2009-12-20 00:57:06 |
|
| [3140] Cogito | 2009-12-29 16:23:34 |
 A negyedik kérdésre adott "ellenpéldám" nem volt jó, mert ekkor A nem véges. Ez a kérdés tehát még megválaszolatlan.
Jenei Attila felvetésére később térek vissza.
|
| Előzmény: [3138] Cogito, 2009-12-29 13:18:17 |
|
| [3139] jenei.attila | 2009-12-29 15:37:00 |
 Hát ez azért így meredek. Szerinted, ha jól értem, lim f=lim f+f', ha f deriválható és x végtelenhez tart. Ezt nem hinném. A számlálóban egyáltalán nem biztos, hogy ex*f(x) végtelenhez tart (pl. f=sin, vagy f 0-hoz tart, akkor bármi lehet a határérték).
|
| Előzmény: [3138] Cogito, 2009-12-29 13:18:17 |
|
|
|
| [3136] lgdt | 2009-12-28 03:10:38 |
 Vegyünk egy olyan helyet, amitől felfelé a derivált legalább egy pozitív konstans. Alkalmazzuk a Langrange-féle középértéktételt a kiválasztott és az összes tőle jobbra lévő helyre: a függvény a kiválasztott ponton átmenő olyan egyenes felett van, melynek meredeksége az említett konstans.
|
| Előzmény: [3135] Lóczi Lajos, 2009-12-28 00:03:42 |
|
|
|
| [3133] Lóczi Lajos | 2009-12-27 22:16:59 |
 Persze, igazad van, a 3. és 4. kérdés most ekvivalens, hiszen az összeg limeszének végességét eleve tudjuk. (A hozzászólásodban nyilván az egyik G helyett F áll mindkét képletben.)
|
| Előzmény: [3132] jonas, 2009-12-27 21:49:07 |
|
|
|
|






 is. Lásd ott :-)
is. Lásd ott :-) 

 f'(x). Mivel viszont a függvény mindenütt deriválható, a Newton-Leibniz szabály miatt
f'(x). Mivel viszont a függvény mindenütt deriválható, a Newton-Leibniz szabály miatt 