| [3280] HoA | 2010-04-30 10:42:01 |
 Tájékozódásul vizsgáljuk a felület metszetét sorra az x=0, y=0, x=y , x= -y síkokkal. A kapott függvények:
f1=y4–y2=y2(y2–1) zérushelyei -1, 0, 1 , a függvény jellegét az origó környezetében az 1. ábra mutatja. Tehát ebben az irányban itt lokális maximum van.
f2=x4–x2=x2(x2–1) hasonló f1 -hez.
f3 : Legyen x=y=t . f3=2t4–4t2=2t2(t2–2) jellegében megegyezik az előzőekkel, csak a zérushelyek itt ( 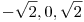 ) )
f4 : Legyen x= -y = t . f4=2t4–2t2+2t2=2t4 A metszetgörbe jellege a 2. ábra szerinti, ebben az irányban lokális minimum van. A felületnek tehát az origó nyeregpontja. Általánosabb eredményt kapunk, ha áttérünk polárkoordinátákra. x=rcos ,y=rsin ,y=rsin helyettesítéssel helyettesítéssel
g(r, )=r4(cos4 )=r4(cos4 +sin4 +sin4 )–r2(cos )–r2(cos +sin +sin )2 Az r szerinti deriváltak az origóban )2 Az r szerinti deriváltak az origóban 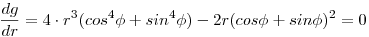 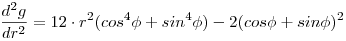 Ez általában negatív és az 1. ábra szerinti viselkedést indokolja. A kivétel éppen az x = -y eset, ekkor a második tag eltünik, és így még a harmadik derivált is nulla. A negyedik derivált pozitív volta adja a 2. ábra szerinti metszetet. Összefoglalásként megállapíthatjuk, hogy az origó ennek a függvénynek egy különleges nyeregpontja, egy irányban lokális minimum, az összes többiben lokális maximum. Ez általában negatív és az 1. ábra szerinti viselkedést indokolja. A kivétel éppen az x = -y eset, ekkor a második tag eltünik, és így még a harmadik derivált is nulla. A negyedik derivált pozitív volta adja a 2. ábra szerinti metszetet. Összefoglalásként megállapíthatjuk, hogy az origó ennek a függvénynek egy különleges nyeregpontja, egy irányban lokális minimum, az összes többiben lokális maximum.
Hátha valaki folytatja e,césv vektorok elemzésével.
|
 |
| Előzmény: [3279] Lóczi Lajos, 2010-04-23 23:34:25 |
|
| [3279] Lóczi Lajos | 2010-04-23 23:34:25 |
 (Szélsőérték szempontjából) milyen típusú pontja az f(x,y):=x4-x2-2xy+y4-y2 felületnek az origó?
|
|
| [3278] HoA | 2010-04-23 17:38:03 |
 Gondolatébresztőnek kezdjük az általános esettel, a térkép hasonlatnál maradva legyen az origó felett közönséges domboldal. Ekkor a szintvonal két irányába mutat v1=v0 és v2=-v0 és ezekre merőleges a gradiens, e=g és c=-g . ( A minusz jelek nálam nem igazán jól látszanak. ) Érdekesebbek a speciális terepalakulatok - csúcs , nyereg, töbör .
|
| Előzmény: [3277] Lóczi Lajos, 2010-04-17 14:04:34 |
|
| [3277] Lóczi Lajos | 2010-04-17 14:04:34 |
 A térbeli x-y-z koordinátarendszerben tekintsünk egy sima "domborzati térképet" az x-y alapsík fölött, azaz legyen adott egy f:R2 R deriválható függvény. Tekintsük az alapsíkban az összes origó kezdőpontú egységvektort, és jelöljük meg ezek közül mindazokat az e, c és v vektorokat, amelyek irányában az f felület origó fölötti f(0) pontjában rendre: legmeredekebb az emelkedés, legnagyobb a csökkenés, illetve a pontbeli adott irányú érintőegyenes vízszintes. R deriválható függvény. Tekintsük az alapsíkban az összes origó kezdőpontú egységvektort, és jelöljük meg ezek közül mindazokat az e, c és v vektorokat, amelyek irányában az f felület origó fölötti f(0) pontjában rendre: legmeredekebb az emelkedés, legnagyobb a csökkenés, illetve a pontbeli adott irányú érintőegyenes vízszintes.
Milyen összefüggések állapíthatók meg az e, c és v vektorok között?
|
|
| [3276] Tóbi | 2010-04-14 15:35:35 |
 Vegyük az egyenlőtlenség logaritmusát. k*log(a)=<L*log(b)<k*log(a)+log(2) Tulajdonképpen itt log(b) olyan többszörösét keressük, amit maradékosan osztva log(a)-val, a maradék legfeljebb log(2) lesz. Amennyiben log(a)/log(b) racionális a maradék 0 is lehet, ha irracionális, tetszőlegesen megközelíti a 0-t, így log(2) alá is megy.
|
| Előzmény: [3272] m2mm, 2010-04-13 23:21:09 |
|
|
|
|
| [3272] m2mm | 2010-04-13 23:21:09 |
 Igaz-e, hogyha a>b>1 a és b valós, akkor létezik pozitív egész k,l, hogy ak<bl<2ak?
|
|
|
|
|
|
|
|
| [3265] Lóczi Lajos | 2010-03-25 22:55:31 |
 Legyen a>0 adott valós szám. Mi lesz n  esetén az esetén az
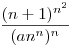
sorozat határértéke?
|
|
|
|
| [3262] Alma | 2010-02-25 17:12:18 |
 Szerintem függ, hogy melyik az az adott elem k-as. Vegyük például azt a leegyszerűsített esetet, hogy a kockának két oldala van: 1,2 és n=3szor dobunk.
Azok a számsorok, melyekben az 11 elemkettes pontosan egyszer fordul elő: 112 és 211.
Azok a számsorok, melyekben a 12 elemkettes pontosan egyszer fordul elő: 112, 121, 122, 212.
A két eseménynek nem egyenlő a valószínűsége.
|
| Előzmény: [3261] Láda19, 2010-02-25 16:21:43 |
|
| [3261] Láda19 | 2010-02-25 16:21:43 |
 Lenne egy valószínűségszámítási probléma, amit a napokban kérdeztek tőlem, de még nem tudtam megoldani. Szeretném, ha valaki segítene.
Egy dobókockával n-szer dobunk, majd a dobások eredményét leírjuk egymás mellé. Mennyi a valószínűsége annak, hogy az 1, 2, 3, 4, 5, 6 számokból képezett, adott elem k-as (k<n) pontosan egyszer előfordul az n hosszúságú számsorban?
|
|
|
|
| [3258] Fálesz Mihály | 2010-02-19 12:41:32 |
 Számomra inkább az érdekes, hogy ezzel a módszerrel primitív gyökök felhasználása nélkül is ilyen röviden be lehet bizonyítani azt, hogy a akkor és csak akkor kvadradikus maradék mod p, ha a(p-1)/2 1(mod p), különben a(p-1)/2 1(mod p), különben a(p-1)/2 -1. -1.
(A kis Fermat-tétel párosítgatás és Wilson-tétel nélkül is kijön a szokásos bizonyítással: összeszorozzuk az a,2a,...,(p-1)a maradékokat.)
|
| Előzmény: [3256] bily71, 2010-02-17 23:30:28 |
|
| [3257] bily71 | 2010-02-18 21:45:01 |
 Én arra jutottam, hogy a le nem fedett számok halmaza végtelen. Gondoltmenetem a következő:
Vonjuk össze az egy modulushoz tartozó számtani sorozatokat, így minden 3-nál nagyobb prímhez kapunk egy olyan számsorozatot, amelyben két differencia váltja egymást. Írjuk fel a sorokat egymás után képzeletben. A sorok táblázatba rendezhetőek, a táblázatban a számok a prímek szorzata egyhatodának alsó, vagy felső egészrészének felelnek meg. Ezt a táblázatot azt hiszem már jól ismerjük.
Ha a le nem fedett számok halmaza véges lenne, akkor létezne k természetes szám, hogy e szám nem, de minden nála nagyobb fedett. Ez csak úgy lehetséges, ha minden új sorozat legkisebb olyan tagja, amely eddig egyik sorozatnak sem volt tagja fedi a k után következő olyan számot, amelyet az előző sorozatok nem fedtek le, (remélem eddig érthetően fogalmaztam).
Jelölje an az n-edik le nem fedett számot, bn pedig az n-edik sorozat azon legkisebb tagját, amely nem szerepelt egyik eddigi sorozatban sem. Mivel a táblázat a főátlóra szimmetrikus, ezért ![a_n<\left[\frac{p_n^2}{6}\right]\le{b_n}](keplet.cgi?k=27E2DD7917EF967E) , ebből következik, hogy an<bn, így soha nem fedheti, mert az an=bn soha nem teljesül. , ebből következik, hogy an<bn, így soha nem fedheti, mert az an=bn soha nem teljesül.
Jól következtettem? Eléggé tömören fogalmaztam, ha nem érthető, bővebben kifejtem.
A nem fedett számok egy nevezetes számsorozat tagjaival egyértelműen megfeleltethetőek .
|
| Előzmény: [3253] bily71, 2010-02-16 20:04:32 |
|
| [3256] bily71 | 2010-02-17 23:30:28 |
 Két eset lehetséges:
1. a nem kvadratikus maradék modulo p. Ekkor a Wilson-tétel miatt
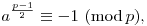
ebből
ap-1 1 (mod p), 1 (mod p),
ebből
ap a (mod p). a (mod p).
2. a kvadratikus maradék modulo p. Ekkor a Wilson-tétel miatt
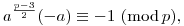
ebből

ebből ugyancsak a kis Fermat-tételt kapjuk.
(Az előző megoldásom második része részben hibás).
|
| Előzmény: [3252] Fálesz Mihály, 2010-02-15 10:16:52 |
|



 ,y=rsin
,y=rsin

 R deriválható függvény. Tekintsük az alapsíkban az összes origó kezdőpontú egységvektort, és jelöljük meg ezek közül mindazokat az e, c és v vektorokat, amelyek irányában az f felület origó fölötti f(0) pontjában rendre: legmeredekebb az emelkedés, legnagyobb a csökkenés, illetve a pontbeli adott irányú érintőegyenes vízszintes.
R deriválható függvény. Tekintsük az alapsíkban az összes origó kezdőpontú egységvektort, és jelöljük meg ezek közül mindazokat az e, c és v vektorokat, amelyek irányában az f felület origó fölötti f(0) pontjában rendre: legmeredekebb az emelkedés, legnagyobb a csökkenés, illetve a pontbeli adott irányú érintőegyenes vízszintes. 

 bl<2ak a kérdéses egyenlőtlenség.
bl<2ak a kérdéses egyenlőtlenség.

 ha a<e, 1 ha a=e és 0 ha a>e.
ha a<e, 1 ha a=e és 0 ha a>e.
 Z és 1
Z és 1 x3 (mod p), ha pedig p=3k+1, a akkor, és csak akkor kubikus maradék, ha a(p-1)/3
x3 (mod p), ha pedig p=3k+1, a akkor, és csak akkor kubikus maradék, ha a(p-1)/3