| [3305] Sirpi | 2010-08-24 11:07:51 |
 ...kivéve, ha q=3 a második esetnél (hogy teljes legyen a bizonyítás). Valamint az összeg párosnál, és 3-mal oszthatónál nem árt megnézni, hogy nem lehet se 2, se 3 (de ez trivi).
|
| Előzmény: [3304] jenei.attila, 2010-08-24 09:18:03 |
|
|
| [3303] D. Tamás | 2010-08-23 10:43:49 |
 Mutassuk meg, hogy ha p és q prímszámok, akkor a pq+qp összeg csak egyetlenegy esetben prímszám, ha p=2 és q=3. (p<q) A feladat egyáltalán nem nehéz, ezt most előre leszögezem.
|
|
| [3302] Róbert Gida | 2010-08-18 17:38:34 |
 Nem azt mondtam, hogy nehéz a megoldása, hanem azt, hogy gyenge a feladatkitűzés.
Amúgy Tóbi megoldása még mindig rossz, azt nem tudom miért tette fel, hogy xi>0 amikor a feladatban természetes egészekről van szó. És ekkor van pontosan egy megoldás, (ha minden xi különböző és n 2): 0!+1!=2!. 2): 0!+1!=2!.
|
| Előzmény: [3298] D. Tamás, 2010-08-17 21:07:40 |
|
| [3301] Tóbi | 2010-08-18 16:00:25 |
 Így sem nehéz a megoldás. Állítás: Ha n 2 rögzített egész, akkor n db faktoriális összege csak véges sok esetben lehet faktoriális. Bizonyítás: Tegyük fel, hogy a legnagyobb tag az összegben (jelölje k!) nagyobb, mint n!. Ekkor az n tag összege k! és (k+1)! közé esik, hiszen n*k!<k*k!<(k+1)!. Véges sok eset kivételével lesz is ilyen nagy a tagok közt. Egyébként valószínűleg tényleg így gondolták eredetileg a feladatot, ez indokolja a "csak véges sok megoldás"-t a szövegben. 2 rögzített egész, akkor n db faktoriális összege csak véges sok esetben lehet faktoriális. Bizonyítás: Tegyük fel, hogy a legnagyobb tag az összegben (jelölje k!) nagyobb, mint n!. Ekkor az n tag összege k! és (k+1)! közé esik, hiszen n*k!<k*k!<(k+1)!. Véges sok eset kivételével lesz is ilyen nagy a tagok közt. Egyébként valószínűleg tényleg így gondolták eredetileg a feladatot, ez indokolja a "csak véges sok megoldás"-t a szövegben.
|
| Előzmény: [3300] Fálesz Mihály, 2010-08-18 13:44:20 |
|
|
|
|
|
|
|
|
|
|
|
| [3290] Sirpi | 2010-07-16 13:35:21 |
 Szerintem elég egyszerűen kijön, hogy ha 0 t t 1, akkor ha a, b, c oldalakból szerkeszthető háromszög, akkor az at, bt, ct oldalakból is, egyéb t értékekre pedig van ellenpélda. 1, akkor ha a, b, c oldalakból szerkeszthető háromszög, akkor az at, bt, ct oldalakból is, egyéb t értékekre pedig van ellenpélda.
Ha 0 t t 1, akkor a 1, akkor a b b c-ből következik, hogy at c-ből következik, hogy at bt bt ct, ezért elég megmutatni, hogy c<a+b-ből következik, hogy ct<at+bt. Mivel c<a+b, így ezt leosztva c1-t-vel: ct, ezért elég megmutatni, hogy c<a+b-ből következik, hogy ct<at+bt. Mivel c<a+b, így ezt leosztva c1-t-vel:
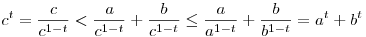
tehát valóban ct<at+bt.
Ha t>1, akkor elég kis epszilonra az 1,1,2- oldalú háromszög megfelelő, viszont az 1t,1t,(2- oldalú háromszög megfelelő, viszont az 1t,1t,(2- )t-re már nem teljesül a háromszög-egyenlőtlenség, mert (2- )t-re már nem teljesül a háromszög-egyenlőtlenség, mert (2- )t>2. )t>2.
Amúgy a t<0 is hasonlóan érdekes eset, arra is van egyszerű ellenpélda (ha  elég kicsi, akkor elég kicsi, akkor  ,1,1 megfelelő háromszög, de ,1,1 megfelelő háromszög, de  t>2). t>2).
|
| Előzmény: [3286] D. Tamás, 2010-07-15 16:05:08 |
|
| [3289] D. Tamás | 2010-07-16 12:19:24 |
 Ha minden igaz, megvan a felső korlát: n 1 Most csupán eredményt közlök, levezetni sem olyan nehéz, mint gondoltam. Azonban az alsó korlát megkeresése már nehezebb lesz úgy vélem. (Legalábbis bizonyítani biztosan az lesz, ha megsejtettük a számot.) 1 Most csupán eredményt közlök, levezetni sem olyan nehéz, mint gondoltam. Azonban az alsó korlát megkeresése már nehezebb lesz úgy vélem. (Legalábbis bizonyítani biztosan az lesz, ha megsejtettük a számot.)
|
|
| [3288] D. Tamás | 2010-07-16 11:45:46 |
 A 2 feladat hasonló, de nem ugyanaz.
B. 3936. Milyen feltételeknek kell teljesülni az a,b,c valós számokra ahhoz, hogy minden n természetes számra létezzék olyan háromszög, amelynek az oldalai an,bn és cn?
Az én feladatom pediog a következő volt: Igaz-e, hogy ha a,b és c oldalakból szerkeszthető (sík)háromszög, akkor an,bn és a cn oldalakból is szerkeszthető háromszög, ha n R\R-? Ez könnyen elmondható, hogy nem igaz, hiszen példának vehetjük a 3 4 és 5 egység hosszúságú oldalakkal rendelkező háromszöget. Ez a példa azért is speciális, mert n=2 esetén megkapjuk az oldalak közti összefüggést: 32+42=52 (De egyébként R\R-? Ez könnyen elmondható, hogy nem igaz, hiszen példának vehetjük a 3 4 és 5 egység hosszúságú oldalakkal rendelkező háromszöget. Ez a példa azért is speciális, mert n=2 esetén megkapjuk az oldalak közti összefüggést: 32+42=52 (De egyébként  pithagoraszi számhármasnál ezt tapasztalhatjuk. Összefoglalva ez a feladat azért más a B.3936-hoz képest, mert itt meg kell keresnünk azokat az n számokat, melyekre igaz lesz, hogy az an,bn és cn hosszúságú szakaszokl szerkeszthető háromszög. n=1 és pithagoraszi számhármasnál ezt tapasztalhatjuk. Összefoglalva ez a feladat azért más a B.3936-hoz képest, mert itt meg kell keresnünk azokat az n számokat, melyekre igaz lesz, hogy az an,bn és cn hosszúságú szakaszokl szerkeszthető háromszög. n=1 és 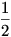 jó eset, de ez nem zárja ki a többi eset létezését. Mivel a probléma egyre jobban érdekel, ezért én is nekiállok a feladatnak mostantól. Bár van egy olyan sejtésem, hogy ez nem egy egyszerű probléma, na de majd meglátjuk. jó eset, de ez nem zárja ki a többi eset létezését. Mivel a probléma egyre jobban érdekel, ezért én is nekiállok a feladatnak mostantól. Bár van egy olyan sejtésem, hogy ez nem egy egyszerű probléma, na de majd meglátjuk.
|
| Előzmény: [3287] psbalint, 2010-07-15 16:52:31 |
|
|
| [3286] D. Tamás | 2010-07-15 16:05:08 |
 Teljesen általánosan is felvetődhet a kérdés: Tehát ha a,b és c oldalakból szerkeszthető (sík)háromszög, akkor an,bn és a cn oldalakból is szerkeszthető háromszög, ha n R\R-.? A válasz nem, de jó feladatnak tűnik - elsőre - megkeresni az n lehetséges értékeit. R\R-.? A válasz nem, de jó feladatnak tűnik - elsőre - megkeresni az n lehetséges értékeit.
|
|
|
|
|
| [3282] Kós Géza | 2010-07-11 20:17:08 |
 Az idei matekolimpián az 5. feladat volt a legérdekesebb, szerintem érdemes itt is megbeszélni.
506. feladat (IMO2010/5). A B1,B2,B3,B4,B5,B6 dobozok mindegyikében kezdetben egy érme van. Kétféle megengedett lépés van:
1. típusú lépés: Választunk egy Bj nemüres dobozt, ahol 1 j j 5. Elveszünk egy érmét a Bj dobozból, és hozzáadunk két érmét a Bj+1 dobozhoz. 5. Elveszünk egy érmét a Bj dobozból, és hozzáadunk két érmét a Bj+1 dobozhoz.
2. típusú lépés: Választunk egy Bk nemüres dobozt, ahol 1 k k 4. Elveszünk egy érmét a Bk dobozból, és kicseréljük a Bk+1 (esetleg üres) doboz tartalmát a Bk+2 (esetleg üres) doboz tartalmával. 4. Elveszünk egy érmét a Bk dobozból, és kicseréljük a Bk+1 (esetleg üres) doboz tartalmát a Bk+2 (esetleg üres) doboz tartalmával.
Állapítsuk meg, hogy ilyen lépések valamilyen véges sorozata segítségével elérhető-e, hogy a B1, B2, B3, B4, B5 dobozok mindegyike üres legyen, a B6 doboz pedig pontosan 201020102010 érmét tartalmazzon. (Definíció szerint abc=a(bc).)
|
|
| [3281] jonas | 2010-05-12 23:13:41 |
 gabor7987 feladata a Valaki monja meg! téma 1024. hozzászólásában annyira megtetszett, hogy föladtam egy nehezebb változatát az idei BME matematika versenyen. A feladat így szól.
505. feladat. Adott két 1-nél nagyobb egész szám: m és n. Bizonyítsuk be, hogy csak véges sok n-edik hatvány áll elő mn egymás utáni egész szám n-edik hatványának az összegeként.
Próbáljátok meg megoldani. Köszönet gabor7987-nak az ötletért, jenei.attilának a megoldás ötletéért, valamint Horváth Miklósnak amiért évek óta fáradhatatlanul szervezi a versenyt.
|
|





 2): 0!+1!=2!.
2): 0!+1!=2!.

 N!
N! t
t oldalú háromszög megfelelő, viszont az 1t,1t,(2-
oldalú háromszög megfelelő, viszont az 1t,1t,(2- pithagoraszi számhármasnál ezt tapasztalhatjuk. Összefoglalva ez a feladat azért más a B.3936-hoz képest, mert itt meg kell keresnünk azokat az n számokat, melyekre igaz lesz, hogy az an,bn és cn hosszúságú szakaszokl szerkeszthető háromszög. n=1 és
pithagoraszi számhármasnál ezt tapasztalhatjuk. Összefoglalva ez a feladat azért más a B.3936-hoz képest, mert itt meg kell keresnünk azokat az n számokat, melyekre igaz lesz, hogy az an,bn és cn hosszúságú szakaszokl szerkeszthető háromszög. n=1 és 

