Fórum: Érdekes matekfeladatok

[1] [2] [3] [4] [5] [6] [7] [8] [9] [10] [11] [12] [13] [14] [15] [16] [17] [18] [19] [20] [21] [22] [23] [24] [25] [26] [27] [28] [29] [30] [31] [32] [33] [34] [35] [36] [37] [38] [39] [40] [41] [42] [43] [44] [45] [46] [47] [48] [49] [50] [51] [52] [53] [54] [55] [56] [57] [58] [59] [60] [61] [62] [63] [64] [65] [66] [67] [68] [69] [70] [71] [72] [73] [74] [75] [76] [77] [78] [79] [80] [81] [82] [83] [84] [85] [86] [87] [88] [89] [90] [91] [92] [93] [94] [95] [96] [97] [98] [99] [100] [101] [102] [103] [104] [105] [106] [107] [108] [109] [110] [111] [112] [113] [114] [115] [116] [117] [118] [119] [120] [121] [122] [123] [124] [125] [126] [127] [128] [129] [130] [131] [132] [133] [134] [135] [136] [137] [138] [139] [140] [141] [142] [143] [144] [145] [146] [147] [148] [149] [150] [151] [152] [153] [154] [155] [156] [157] [158] [159] [160] [161]

Szeretnél hozzászólni? Jelentkezz be.

[1157] Lóczi Lajos	2006-01-13 18:55:41
Nem pongyolán, csak többértelműen, pont azért írtam ezt :) Az együtthatók racionális volta is burkolt feltevés?
Előzmény: [1154] Iván88, 2006-01-13 14:26:13

[1156] nadorp

2006-01-13 18:35:29

$(x-2)(x^2+\frac12)=x^3-2x^2+\frac12x-1$

Van racionális gyöke ( x=2), az első és utolsó tag együtthatója $\pm$ 1, és sem az 1,sem a -1 nem gyöke.

Előzmény: [1155] Iván88, 2006-01-13 14:37:40

[1155] Iván88

2006-01-13 14:37:40

Szia Viktor!

A válaszod jó, de nem egészen ez volt a kérdés.

Mivel a polinom fokszáma páratlan, és $\pm$ x^2a+1+... $\pm$ 1 alakú, ezért valóban csak az 1 és a -1 lehet valós gyöke. A -1 mindenképpen az (hogy az 1 is, azt nem tudni), mert van valós gyöke. Értelemszerűen ekkor a -1 reciproka is gyöke az egyenletnek, ekkor viszont ez egy szimmetrikuspoéinom. (Amiből az is következik, hogy az első és utolsó tag előjele megegyezik)

Előzmény: [1152] xviktor, 2006-01-12 21:13:41

[1154] Iván88

2006-01-13 14:26:13

Kedves Lajos.

Lehet, hogy pongyolán fogalmaztam, de az általad leírt képletnem illik ide, mert itt az utolsó tag együtthatója a 0, míg az elsőé az 1.

Előzmény: [1153] Lóczi Lajos, 2006-01-12 23:02:48

[1153] Lóczi Lajos

2006-01-12 23:02:48

Nézd a következő példát:

x³+ $\pi$ x²+x=0, melynek egyetlen racionális gyöke a 0.

Előzmény: [1152] xviktor, 2006-01-12 21:13:41

[1152] xviktor

2006-01-12 21:13:41

Hali!

Horner-> ha van racionalis gyoke-> elso es utolso tag osztoinak hanyadosa lehet-> $\pm$ 1 lehet csak racionalis gyok. A tobbi lehet irracionalis vagy komplex...

Udv: Viktor

Előzmény: [1151] Iván88, 2006-01-12 20:59:30

[1151] Iván88

2006-01-12 20:59:30

Nem egészen jól fel a kérdést:

A polinom többi tagjáról mit lehet elmondani? (ha nem lehet, miért nem?)

Előzmény: [1148] Iván88, 2006-01-12 19:30:23

[1150] xviktor	2006-01-12 20:51:11
Amit elobb elfelejtettem leirni: mas racionalis gyok ezen kivul nem lehet.
Előzmény: [1149] xviktor, 2006-01-12 20:46:08

[1149] xviktor

2006-01-12 20:46:08

A racionalis gyok $\pm$ 1.

Udv: Viktor

Előzmény: [1148] Iván88, 2006-01-12 19:30:23

[1148] Iván88

2006-01-12 19:30:23

212. feladat:

Egy páratlan fokszámú polinom első és utolsó együtthatója $\pm$ 1. Mit állíthatunk a polinomról, ha van racionális gyöke?

[1147] Iván88	2005-12-31 23:50:08
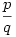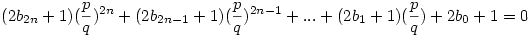Sziasztok! Szép a feladat. Legyen a szóban forgó polin0m p(x). p(x)=a_2nx²ⁿa_2n-1x^2n-1+...+a₂x²+a₁x+a₀, ahol a_i konstansok. Mivel a_i páratlan, ezért a_i=2b_i+1 alakba hozható. (i=0;1;...;2n) Indirekt bizonyítás: Legyen x= $\frac{p}{q}$ , ahol p,q (nem 0)egészek és relatív prímek. $(2b_{2n}+1)(\frac{p}{q})^{2n}+(2b_{2n-1}+1)(\frac{p}{q})^{2n-1}+...+(2b_1+1)(\frac{p}{q})+2b_0+1=0$ . Szorozzunk be q²n-nel: (2b_2n+1)p²ⁿ+(2b_2n-1+1)p^2n-1q+...+(2b₁+1)pq^2n-1+(2b₀+1)q²ⁿ=0. 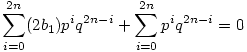Ha kibontjuk a zárójeleket akkor azt kapjuk, hogy $\sum_{i=0}^{2n}(2b_1)p^iq^{2n-i}+\sum_{i=0}^{2n}p^iq^{2n-i}=0$ . Az első tag a 2-es szorzó miatt mindig páros. Nézzük a másodikat: p és q közül legfeljebb az egyik páros (mert relatív prímek) ekkor, ha p is, q is páratlan, akkor a második tag is páratlan, mivel 2n+1 értéket adtunk össze. Ha az egyig páros akkor is páratlan az összeg mert ekkor a második tagban 2n db. báros, és egy páratlan (amikor a páros szám a 0. hatványon szerepel, így az értéke 1) számot adtunk össze. Vagyis a második tag mindkét esetben páratlan, ekkor azonban az összegnek is páratlannak kell lennie, ami ellentmondás, mert a 0 egy páros szám. Azt kaptuk, hogy a racionális számok halmazán valóban nincs megoldás. Q.E.D.
Előzmény: [1146] Csimby, 2005-12-10 23:37:29

[1146] Csimby	2005-12-10 23:37:29
211. feladat Biz. be, hogy ha egy páros fokú polinom minden együtthatója páratlan egész, akkor a polinomnak nincsen racionális gyöke.

[1145] Yegreg

2005-12-06 17:35:29

A feladat átfogalmazható úgy is, hogy a csoporton belülire vezető élek száma bármely csúcsnál legfeljebb egy.

Oszzuk két csoportba a csúcsokat tetszőlegesen! Ha a kívánt elrendezés lép fel, akkor készen vagyunk, ha nem, akkor van olyan csúcs, amelyből a saját csoportjába vezető élek száma legalább kettő, ez azt jelenti, hogy a másik csoportba vezető él(ek :)) száma legfeljebb egy, hiszem minden pont foka legfeljebb három. Ekkor a következőt tesszük: ezt a csúcsot áthelyezzük a másik halmazba. Ezzel ezen csúcs korábbi csoportjában legalább 2-vel csökkent, új csoportjában pedig legfeljebb 1-gyel nőtt a csoporton belüli összes él száma, ez azt jelenti, hogy ez a lépés csökkenti a két csoport összes csoporton belüli éleinek számát.

Ha ezzel a lépéssel a kívánt helyzethez jutunk, akkor kész, ha nem, akkor folytatjuk az eljárást.

Mivel az eljárások során a két csoport összes csoporton belüli éleinek száma szigorúan monoton csökken, és ha nem a kívánt helyzet áll fennt, akkor biztosan folytathatjuk az eljárást, ezért következik, hogy egyszer biztosan véget ér, hiszen az két csoport összes csoporton belüli éleinek száma természetes szám mindig, és pl. 0-nál triviálisan a kívánt helyzet alakul ki.

Ennek a feladatnak viccesebb változata, amikor a politikusok vágják pofon egymást...:)

Üdv:

Szűcs Gergely

[1144] Csimby	2005-12-05 16:16:32
210. feladat Bizonyítsuk be, hogy ha egy gráfban minden pont foka legfeljebb 3, akkor a gráf csúcsai két részre oszthatóak úgy, hogy ha a két rész között menő éleket töröljük, minden pont foka legfeljebb 1 lesz.

[1143] Lóczi Lajos	2005-11-29 15:28:22
Igen, ilyesmire gondoltam én is, tehát az algebra alaptétele itt minden további nélkül nem igaz.
Előzmény: [1142] jonas, 2005-11-28 21:17:56

[1142] jonas	2005-11-28 21:17:56
Vagy ix-xi=i.
Előzmény: [1141] jonas, 2005-11-28 21:15:34

[1141] jonas	2005-11-28 21:15:34
Talán ix+xi=j?
Előzmény: [1139] Lóczi Lajos, 2005-11-17 19:30:54

[1140] jonas

2005-11-28 19:42:12

Van pár diszkrét matek feladatom. Feladom őket itt, hátha valakit érdekel.

209. Legyen s₀=0; s₁,P,Q tetszőleges egészek. Definiáljuk az s_n sorozatot az s_n+1=Ps_n-1+Qs_n rekurzióval.

Lássuk be, hogy ekkor minden n,k egészre

(s_n,s_k)=s_(n,k)

ahol (n,k) jelöli a két szám legnagyobb közös osztóját. Speciális esetként s_k osztója s_n-nek akkor és csak akkor, ha k osztja n-et.

Érdemes megnézni, milyen sorozatokat kapunk s₁=P=Q=1 illetve az s₁=1,P=-2,Q=3 esetén.

A másik két feladatot majd később feladom, ha van érdeklődés (a nevek a másodikban Catalan és Hankel, a harmadikban Catalan és Csebisev).

[1139] Lóczi Lajos	2005-11-17 19:30:54
208. feladat. Adjunk példát olyan (pontosan) elsőfokú egyenletre, aminek nincs megoldása a kvaterniók között.

[1138] Lóczi Lajos	2005-11-17 19:16:27
Igen, itt is az 1/2 bukkant fel. (De a legjobban arra lennék kíváncsi, hogy ennek vajon van-e bármiféle köze ahhoz az eredményhez, ami az "ujjgyakorlatok" 88-as feladatában fog kijönni: "szimmetria és extrémum" egybeesése, amire más helyeken is sok példát láttam már...)
Előzmény: [1137] nadorp, 2005-11-17 11:43:02

[1137] nadorp

2005-11-17 11:43:02

Biztos van elemibb megoldás is,ez a következőt használja:

Ha 0<x<1, akkor nyilván

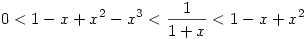$0<1-x+x^2-x^3<\frac1{1+x}<1-x+·x^2$ ,azaz mindkét oldalt 0-tól x-ig integrálva

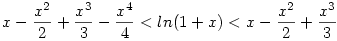
$x-\frac{x^2}2+\frac{x^3}3-\frac{x^4}4<ln(1+x)<x-\frac{x^2}2+\frac{x^3}3$

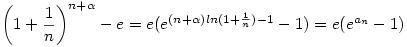$\left(1+\frac1n\right)^{n+\alpha}-e=e(e^{(n+\alpha)ln(1+\frac1n)-1}-1)=e(e^{a_n}-1)$ . Mivel az e^x függvény szigorúan monoton nő,a 0-ba történő konvergencia sebességét nyilván az dönti el, hogy a_n milyen gyorsan tart nullába.

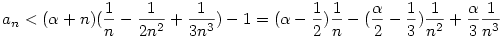$a_n<(\alpha+n)(\frac1n-\frac1{2n^2}+\frac1{3n^3})-1=(\alpha-\frac12)\frac1n-(\frac\alpha2-\frac13)\frac1{n^2}+\frac\alpha3\frac1{n^3}$ .

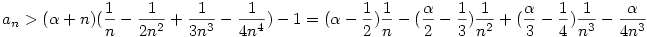$a_n>(\alpha+n)(\frac1n-\frac1{2n^2}+\frac1{3n^3}-\frac1{4n^4})-1=(\alpha-\frac12)\frac1n-(\frac\alpha2-\frac13)\frac1{n^2}+(\frac\alpha3-\frac14)\frac1{n^3}-\frac{\alpha}{4n^3}$ .

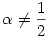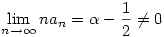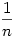Látszik, hogy ha $\alpha\neq\frac12$ ,akkor $\lim_{n\to\infty}na_n=\alpha-\frac12\neq0$ ,azaz a_n konvergenciájának nagyságrendje $\frac1n$ ,

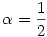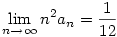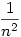$\alpha=\frac12$ esetén pedig $\lim_{n\to\infty}n^2a_n=\frac1{12}$ ,azaz a_n konvergenciájának nagyságrendje $\frac1{n^2}$ és ez gyorsabb.

Előzmény: [1133] Lóczi Lajos, 2005-11-16 12:19:00

[1136] xviktor

2005-11-16 17:50:57

Az x_n sorozat hatarerteke vegtelenben $\frac12$ .

Udv: Viktor

Előzmény: [1135] Sirpi, 2005-11-16 16:46:50

[1135] Sirpi	2005-11-16 16:46:50
Na jó, kifejezem x_n-et: $x_n = \frac1{\ln(1+\frac1n)}-n$ , ennek kellene a határértéke.
Előzmény: [1134] Sirpi, 2005-11-16 12:57:54

[1134] Sirpi

2005-11-16 12:57:54

Ezt a problémát már régebben én is kitaláltam. Én úgy oldottam meg, hogy definiáltam a következő x_n sorozatot: 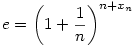$e = \left(1+\frac1n \right)^{n+x_n}$

Ekkor az x_n sorozat konvergens, és a határértékét nem mondom meg egyelőre :-)

Bár úgy érzem, a kétféle megközelítés ugyanarra az eredményre vezet, de be kéne látni, hogy ez tényleg így is van.

Előzmény: [1133] Lóczi Lajos, 2005-11-16 12:19:00

[1133] Lóczi Lajos

2005-11-16 12:19:00

Vizsgáljuk tovább az "ujjgyakorlatok"-ban előkerült sorozatot. Legyen $\alpha$ $\in$ [0,1] rögzített és tekintsük az $\left(1+\frac{1}{n}\right)^{n+\alpha}$ sorozatot, amelyről tudjuk, hogy $\alpha$ -tól függetlenül e-hez tart.

207. feladat. Mely $\alpha$ esetén lesz a konvergenciasebesség a leggyorsabb, azaz mely $\alpha$ esetén tart az

$\left(1+\frac{1}{n}\right)^{n+\alpha}-e$

sorozat leggyorsabban 0-hoz?

Már regisztráltál?
Új vendég vagy?