| [144] Pach Péter Pál | 2003-12-04 11:03:03 |
 Megoldást írok a 13.feladatra.
Azt kellett bizonyítanunk, hogy:
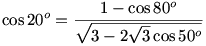
Először is, a jobboldal nevezőjében a gyök alatt pozitív szám van, és így mindkét oldalon értelmes kifejezés áll, hiszen:
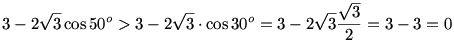
A nevezővel való átszorzás után mindkét oldalon nemnegatív szám áll, így a négyzetre emelés ekvivalens lépés:
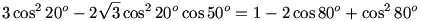
Az a célunk, hogy mindkét egyik oldalon se szerepeljen szögfüggvények szorzata. Ehhez az ismert azosságokat fogjuk használni:
2cos220o=1+cos 40o
2cos220ocos 50o=(1+cos 40o)cos 50o=cos 50o+cos 50ocos 40o=
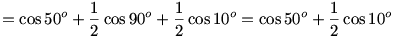
2cos280o=1+cos 160o=1-cos 20o
Ezeket beírva, és az egyenletet 2-vel szorozva a következőket kapjuk:
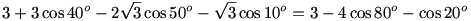
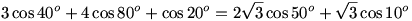
Mivel  , ezért: , ezért:
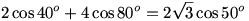
Ez valóban igaz, ugyanis:
2cos 40o+4cos 80o=2cos 40o+2cos 80o+2cos 80o=4cos 60ocos 20o+2cos 80o=2cos 20o+2cos 80o=
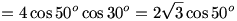
Végig ekvivalens állításokat hajtottunk végre, így bizonyítottuk az eredeti állítást.
|
| Előzmény: [65] Lóczi Lajos, 2003-11-13 18:57:33 |
|
| [143] lorantfy | 2003-12-04 08:44:23 |
 Kedves Gyuri!
Szerintem az a gond a gondolatmenettel, hogy nem feltételezhetjük, hogy aznap este még életben van az elitélt, mert lehet, hogy aznap reggel már kivégezték. Tehát, ha pl. szombat reggel kivégzik, akkor nyugodtan lehetne vasárnap a kivégzés (de akkor már minek). Valójában a gondolatmenet igy szól: Ha szombat reggel nem végeznek ki, akkor szombat este még élek, így tudom, hogy a kivégzés már csak vasárnap lehet, tehát az utolsó nap amikor kivégezhetnek a szombat.
A kiinduló feltételezésnek nincs semmi alapja.
Na eddig jutottam vele.
|
| Előzmény: [133] Gyuri, 2003-12-03 01:21:26 |
|
| [142] lorantfy | 2003-12-04 00:37:11 |
 34.a) megoldása:
Legyen m az 1000 Ft-ossal fizetők száma.
1. Legyen m 0,1n 0,1n
Legrosszabb esetben sajnos ez az m ember a sor elején áll és 1000 Ft-ossal fizetne. Ha tartani akarjuk a 90%-os eladást akkor ezek közül csak 0,1n nem vehet könyvet. Tehát k=m-0,1n db 500 Ft-ossal kell indulni.
2. Ha m 0,1n 0,1n
Ekkor pedig biztos, hogy meglesz a 90%, nem kell befektetés.
Hát ez túl egyszerű közelítés. Nincs mit optimalizálni, ha ragaszkodunk a 90 %-os eladáshoz.
|
| Előzmény: [141] lorantfy, 2003-12-03 22:00:56 |
|
| [141] lorantfy | 2003-12-03 22:00:56 |
 Kedves Éva!
Én elsőre még jobban egyszerűsíteném a problémát.
34.a) feladat Legyen n db műsorfüzet amit el akarunk adni és pontosan n ember aki füzetet szeretne venni. Mindenkinek vagy csak 1000 vagy csak 500 Ft-ja van. Mindenki csak egyszer próbál füzetet venni, ha nem tudunk visszaadni, akkor NEM vesz. Legyen a befektetés k db 500 Ft-os, amivel indul az üzlet.
Mennyi legyen a befektetés - k - minimális értéke, ha a füzeteknek legalább 90 %-át el akarjuk adni.
(Ez szerintem így megoldható.)
További apróságok: Minden vevővel külön foglalkozunk, tehát nem lehet pl. két embernek eladni két füzetet, úgy hogy egyikük fizet 1000 Ft-ot. Nyugodtan képzelhetjük úgy, hogy mi egy asztalnál áruljuk az n db füzetet, az a vevők szépen sorban odajönnek és megpróbálnak vásárolni. Ha 500 Ft-juk van simán megveszik, ha 1000 Ft-juk van és tudunk visszaadni szintén megveszik, viszont ha 1000 Ft-juk van és éppen elfogyott az 500-asunk akkor nem vesznek.
(Lehet először kis n-ekkel próbálkozni, vagy programot irni rá, vagy EXCEL Solver!)
|
| Előzmény: [138] Ratkó Éva, 2003-12-03 14:33:47 |
|
| [140] BrickTop | 2003-12-03 16:39:13 |
 Találtam egy olyan módszert, amivel csak 1 halott lesz a fekete-fehér sapkás feladatban.
A raboknak meg kell beszélniük, hogy az első valamelyik színű sapkák párosságát jelezze. Szóval, mondjuk megbeszélik, hogy ha páros számú fekete sapkát lát, akkor azt mondja, hogy "fekete". Ha páratlant, akkor "fehér"-et mond. Az utána következő ember újból megszámolja a fekete sapkákat, és ebből ki tudja következtetni, hogy fekete sapka van-e rajta. Ha az első elítélt mondjuk "fekete"-t mond, akkor tudja, hogy a mögötte álló ember páros db. fekete sapkát látott. Így ha ő is párosat lát, akkor rajta biztos, hogy fehér van. Ha páratlant lát, akkor ő volt az egyik fekete. A 3. rab természetesen figyeli, hogy mit mondott az előtte álló, és ennek alapján ő is el tudja dönteni, hogy milyen színű sapkája van.
|
| Előzmény: [131] Gyuri, 2003-12-03 00:29:47 |
|
| [139] Hajba Károly | 2003-12-03 14:43:22 |
 33. válasz:
Ki tette fel ezt a feladatot!
MindenKi tudja, ki tette fel ezt a feladatot!
Vagyok, aKi vagyok (... mondá az Úr. :o)
Csak egy valaKi nevében léphetek be a FÓRUM-ba!
??
:o)
|
| Előzmény: [137] Ki, 2003-12-03 13:54:07 |
|
| [138] Ratkó Éva | 2003-12-03 14:33:47 |
 34. feladat: Az első feladat a feladat pontos megfogalmazása. Az egyik budapesti színházban árulnak az előadások szünetében (meg előtte) az adott előadásról szóló ismertető füzetet. Többen panaszkodtak, hogy a jegyszedő nénik (ők árusítják) általában nem tudnak visszaadni. Vegyük a legegyszerűbb esetet: a füzet 500 Ft, és mindenkinél csak 500 vagy 1000 Ft-os bankjegy van. Mennyi 500-assal lássuk el a jegyszedőket, hogy nagy valószínűséggel aki akar, tudjon füzetet venni?
A problémák: valamit kéne tudni arról, hogy mennyi eséllyel van valakinél "apró", és hogy előreláthatóan hányan vennének füzetet - biztos, hogy függ ezektől az eredmény. Mi legyen az a "nagy valószínűséggel"? Van 2000, 5000 Ft-os is (a többiről nem is beszélve). És van 400, 650 Ft-os ismertető füzet...
Én ennyire jutottam, arra azért lesz időm, hogy nyomon kövessem magasröptű eszmecseréteket. (Gondolom, az egyszerűbb feladat pontos megfogalmazásától majd megoldásától a bonyolultabbakéig fokozatosan el lehet jutni.)
Hajrá!
|
|
| [137] Ki | 2003-12-03 13:54:07 |
 33.feladat: Ki tette fel ezt a faladatot!?
Csak egy valaki tudja ki tette fel ezt a feladatot!?
Ha Te tudod ki tette fel ezt a feladatot, akkor Te ki vagy!?
Tehát ki nevében léphetsz be a FÓRUM-ba!?
Ha tudod a jelszót, ami válasz a kérdésre, hogy ki tette fel ezt a feladatot?
|
|
| [136] Gyuri | 2003-12-03 13:29:55 |
 Kedves Onugor!
Valoban, nem feltetlenul kapnak a rabok ugyanannyi feher illetve fekete szinu sapkat, hisz ez nem derul ki a bortonorok felhivasabol, ahogyan az sem, hogy a bortonorok mikor ertekelik a valaszokat. Segitsegul elarulom, hogy ettol nem fugg a feladat megoldasa, azaz a kiszabadithato rabok maximalis szama. Mindezektol fuggetlenul pontositom a feladatot.
kiegeszites a 31. feladathoz: A rabok nem tudjak elore, hogy hany fekete es hany feher sapkat kapnak. A bortonorok pedig csak az osszes felelet elhangzasa utan informaljak a rabokat.
Udv: Gyuri
|
| Előzmény: [135] Hajba Károly, 2003-12-03 12:15:01 |
|
| [135] Hajba Károly | 2003-12-03 12:15:01 |
 Kedves Gyuri!
Ha jól sejtem nem feltétlenül 50 fekete és 50 fehér sapkát húznak a fejükre ill. az időben előttük nyilatkozók helyes v. helytelenségét figyelembe tudják venni.
Hajba Károly
|
| Előzmény: [131] Gyuri, 2003-12-03 00:29:47 |
|
| [134] lorantfy | 2003-12-03 08:28:48 |
 Kedves Károly és Fórumosok!
Igyekeztem a feladatot egyértelműen megfogalmazni, de úgy látszik nem sikerült.Elnézést! Most pontosítok:
Az ábra egy esetet mutat a lehetséges esetek közül.
b) Ha a feltétel nem teljesül, a rab nem szólal meg. Ekkor a következő jön. A 3. rab után újra az 1. rab következik.
|
| Előzmény: [130] Hajba Károly, 2003-12-03 00:07:57 |
|
| [133] Gyuri | 2003-12-03 01:21:26 |
 Kicsit megmozgatta a fantaziamat a borton, ime meg egy orokzold. Itt mar nem csak matematikarol van szo, talan.
32. feladat: az elitelt egy hete
A megrogzott bunozore a birosag a legszigorubb iteletet szabja ki. A biro a buntettek kulonos sulyossaga es nagy szama miatt meggondolatlanul (vagy eppen jol megfontoltan) megprobalja meg nehezebbe tenni az elitelt eletenek utolso nehany napjat. A kovetkezokeppen fogalmazza meg a buntetest: Ma vasarnap van. A kovetkezo het valamelyik napjan reggel 8 orakor lesz a kivegzes. De hogy pontosan melyik nap, azt csak a kivegzes napjan reggel 6 orakor tudhatja meg az elitelt leghamarabb; ha ugyanis hamarabb tudomast szerezne a kivegzes idopontjarol, nem vegezheto ki. KOPP! A bunozo -gondolva, hogy hamarosan bucsut mondhat ennek a vilagnak- szomoruan ballag vissza cellajaba, ahol mar varja -feltunoen vidaman- egyik ugyvedje. Az ugyved a kovetkezo ervelessel all elo: On megmenekult. Elmondom, miert. Ha Ont vasarnap akarnak kivegezni, akkor szuksegkeppen szombat estig eletben kell tartaniuk. Ha tehat On szombat este meg el, biztos lehet benne, hogy vasarnap akartak kivegezni, hisz mas alkalmas nap mar nem adodik. Igy az itelet szerint el kell vessek megiscsak a vasarnapi kivegzes otletet, hisz On erre mar szombat este rajonne. Roviden szolva, Ont nem vegezhetik ki vasarnap. Ha Ont szombaton akarnak kivegezni, akkor szuksegkeppen pentek estig eletben kell tartaniuk. Ha tehat On pentek este meg el, biztos lehet benne, hogy szombaton akartak kivegezni, hisz azt mar elozoleg belattuk, hogy a vasarnap nem johet szoba, igy csak a szombat maradna. Igy az itelet szerint el kell vessek megiscsak a szombati kivegzes otletet. ... Ha Ont hetfon akarnak kivegezni, akkor On ezt mar elore tudna, hisz mar kizartuk a keddet, a szerdat, ..., a vasarnapot. Igy tehat a hetfo is kizarva. Ont nem vegezhetik ki egyetlenegy napon sem! A tortenetnek szomoru vege szakad, mikor csutortok reggel az ugyved legnagyobb meglepetesere az eliteltet kivegzik.
Kerdesek: Igaza volt-e az ugyvednek? Helyesen jartak-e el a vegrehajtok?
Megjegyzes: Ha valaki tarsasagban hosszantarto vitat szeretne kirobbantani, megfelelo modszer a fenti feladat kozzetetele. :)
udv: Gyuri
|
|
| [132] Hajba Károly | 2003-12-03 00:46:20 |
 Az eddig még megoldatlan korábbi feladatok:
12. - [60]
13. - [65]
26. - [112]
27. - [113]
Továbbá a más topikba küldött méricskélős feladatok, de a megoldásokat abban a topikba adjátok.
Hajba Károly
|
|
| [131] Gyuri | 2003-12-03 00:29:47 |
 31. feladat: rabok sapkai 2
Bizonyara ez is sokak altal ismert, de igencsak passzol ide.
A bortonorok unalmukban, vagy talan a kozelgo Karacsonyra valo tekintettel egy jatekot eszelnek ki az intezmenyben sinylodo 100 embertarsuk szamara. Igy hangzik a jatekra valo felhivas: Holnap sorba allitunk benneteket, mindenki csak az elotte allokat fogja latni. Mindenki kap a fejere egy-egy sapkat is, mely vagy feher vagy fekete lesz. Mindenki csak egyszer szolalhat meg, es csak e ket szin egyiket mondhatja. Ahanyan eltalajak a fejukon levo szint, szabadok. Mit javasoljunk a szerencsetleneknek, ha a biztosan megszabadulok szamat akarjuk maximalizalni?
Udv: Gyuri
|
|
| [130] Hajba Károly | 2003-12-03 00:07:57 |
 Kedves László!
Nem veszünk össze a 29-es számon, s hogy félreértés se essen belőle, gyorsan megoldom. :o)
a)
Ha (1) és (2) fehér sapkát viselt volna, (3) azonnal szólna: én fekete vagyok.
Mivel (3) nem szól azonnal, így (1) és (2) is tudja, hogy nem lehetnek mindketten fehérek. Mivel (2) látja a fehér sapkát, ő csak fekete lehet és a biztos információ tudatában szól: én fekete vagyok és szabad.
Ha (1) fekete lenne, (2) nem lenne biztos információ tudatában és nem szólna. Mivel mégis szólt és nem vitték vissza a cellába, (1) tudja, hogy ő fehér és szól: én fehér vagyok, de elkéstem.
Mivel (3) nemszólalásából csak (1) és (2) kapott számukra nem ismert információt, így szegény (3) hoppon maradt új információ terén. Az ő esélye 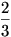 a feketére és a feketére és 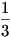 a fehérre. Így (3) nem tippel. a fehérre. Így (3) nem tippel.
b)
(1)-nek 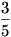 esélye van a fekete sapkára, így visszaviszik dupla büntetéssel. (2)-nek esélye van a fekete sapkára, így visszaviszik dupla büntetéssel. (2)-nek 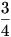 esélye van a feketére és kiszabadul. (3)-nak esélye van a feketére és kiszabadul. (3)-nak 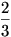 esélye van a fekete sapkára, de későn jutott szóhoz. esélye van a fekete sapkára, de későn jutott szóhoz.
Üdv: HK
|
| Előzmény: [128] lorantfy, 2003-12-02 21:42:13 |
|
| [129] lorantfy | 2003-12-02 22:50:07 |
 Kedves Károly!
Most veszem észre, hogy rosszul számoztam az előző feladatot és így „felülírtam” a Te példádat. Most beírok egy megoldást és majd egyezkedünk a 29-es számon.
Egy személynek 2 nagymamája, 2 nagyapja, 4 dédmamája és 4 dédapja van a családfán.
29.a) Nagymamáink dédapjai: 2 nagymamánknak összesen 8 dédapja van.
Dédmamáink nagyapjai: 4 dédmamánknak összesen 8 nagyapja van.
29.b) Összesen persze nem 16-an vannak, mert közöttük van 4 azonos személy.
A nagymamák édesanyjai dédmamák, így a nagymamák anyai ágon vett dédapjai egyben a dédmamák nagyapjai. Ők nagymamánként ketten vannak, összesen négyen.
Tehát a nagymamáink dédapjai és a dédmamáink nagyapjai összesen 12-en vannak
|
| Előzmény: [121] Hajba Károly, 2003-12-01 11:35:26 |
|
| [128] lorantfy | 2003-12-02 21:42:13 |
 Kedves Károly!
Nagyon tetszik a megoldás „előadása”. Én is be akartam írni, de így nem sikerült volna.
Mondok inkább egy másik feladatot, ami erről jutott eszembe:
29. feladat:
Karácsonykor a börtönigazgató, aki nagyon szereti a logikai feladatokat magához rendeli a három legdörzsöltebb rabot. Sorba állítja őket egymás után és mutat nekik 5 sapkát, 3 fekete színűt és 2 fehéret és ezt mondja nekik: - Most bekötöm a szemeteket és mindegyikőtök fejére felteszek egy sapkát az 5 közül. A maradék sapkákat elteszem, majd leveszem a kötést a szemetekről. Aki először megmondja milyen sapka van a saját fején, az kiszabadul. Aki viszont rosszat mondana, annak megduplázom a büntetését.
Kérdés: Mennyi az egyes rabok kiszabadulásának valószínűsége? Ha:
a): A rabok nagyon unják már a börtönt, így nem kockáztatják meg a dupla büntetést!
b): A rabok tippelnek, de csak akkor, ha 50 %-nál nagyobb ez esélye, hogy a tipp bejön. Itt a rabok a sorszámuk sorrendjében szólalhatnak meg. A rosszul tippelő rab visszamegy a cellájába, a másik kettő (a tippelés eredményét ismerve) tovább játszik.
(Az első rab nem látja a másik kettőt. A középső látja az első sapkáját. A hátsó látja mindkét előtte álló sapkáját. (A saját sapkáját egyik sem látja!)).
|
 |
| Előzmény: [127] Hajba Károly, 2003-12-02 01:19:59 |
|
| [127] Hajba Károly | 2003-12-02 01:19:59 |
 Kedves Gyuri!
Ez egy igazi érdekes matekfeladat, gratula! Legyen  , aki a szorzatot látja, és , aki a szorzatot látja, és  , aki az összeget látja. S úgy tűnik, a végeredmény attól függ, ki kezdte a párbeszédet, mivel erről nincs infónk. , aki az összeget látja. S úgy tűnik, a végeredmény attól függ, ki kezdte a párbeszédet, mivel erről nincs infónk.
1)
 : [Többféleképpen tudom a számot szorzattá bontani,] nem tudom. : [Többféleképpen tudom a számot szorzattá bontani,] nem tudom.
 : [Mivel nem tudja, : [Mivel nem tudja,   1 v. prím; többféleképpen tudom a számot összeggé bontani,] nem tudom. 1 v. prím; többféleképpen tudom a számot összeggé bontani,] nem tudom.
 : [Mivel nem tudja, : [Mivel nem tudja,   2, 3, 4; még mindig többféleképpen tudom a számot szorzattá bontani,] nem tudom. 2, 3, 4; még mindig többféleképpen tudom a számot szorzattá bontani,] nem tudom.
 : [Mivel nem tudja, továbbá : [Mivel nem tudja, továbbá   4; még mindig többféleképpen tudom a számot összeggé bontani,] nem tudom. 4; még mindig többféleképpen tudom a számot összeggé bontani,] nem tudom.
 : [Mivel nem tudja, továbbá : [Mivel nem tudja, továbbá   5; s mivel 5; s mivel  =6 egyik tagjához tartozó összeget kizártuk,] tudom. =6 egyik tagjához tartozó összeget kizártuk,] tudom.
 : [Mivel tudja, : [Mivel tudja,  =6, s mivel =6, s mivel  =7,] tudom. =7,] tudom.
A=1, B=6
2)
 : [Többféleképpen tudom a számot összeggé bontani,] nem tudom. : [Többféleképpen tudom a számot összeggé bontani,] nem tudom.
 : [Mivel nem tudja, : [Mivel nem tudja,   2, 3; többféleképpen tudom a számot szorzattá bontani,] nem tudom. 2, 3; többféleképpen tudom a számot szorzattá bontani,] nem tudom.
 : [Mivel nem tudja, : [Mivel nem tudja,   1 v. prím; még mindig többféleképpen tudom a számot összeggé bontani,] nem tudom. 1 v. prím; még mindig többféleképpen tudom a számot összeggé bontani,] nem tudom.
 : [Mivel nem tudja, továbbá : [Mivel nem tudja, továbbá   4; még mindig többféleképpen tudom a számot szorzattá bontani,] nem tudom. 4; még mindig többféleképpen tudom a számot szorzattá bontani,] nem tudom.
 : [Mivel nem tudja, : [Mivel nem tudja,   4, s mivel 4, s mivel  =5 egyik tagjához tartozó összeget kizártuk,] tudom. =5 egyik tagjához tartozó összeget kizártuk,] tudom.
 : [Mivel tudja, továbbá : [Mivel tudja, továbbá  =5; s mivel =5; s mivel  =6 egyik tagjához tartozó összeget kizártuk,] tudom. =6 egyik tagjához tartozó összeget kizártuk,] tudom.
A=2, B=3
Remélem, minden esetet figyelembe vettem, mivel nagyon leizzadtam. :o)
HK
|
| Előzmény: [123] Gyuri, 2003-12-01 14:32:15 |
|
|
| [125] jenei.attila | 2003-12-01 16:59:22 |
 Kedves László!
Csatlakozok Gyuri megjegyzéséhez, hozzátéve, hogy az egyenletrendszer szimmetriáját nyilván úgy értetted, hogy adott gyökök mellett ezek bizonyos permutációi is megoldást adnak. A feladatban jól látszik, hogy összesen három (az identitást is belevéve) megfelelő permutáció létezik. Ez azonban nem jelenti azt, hogy a gyökök egyenlők.
|
| Előzmény: [119] lorantfy, 2003-12-01 09:05:35 |
|
| [124] Gyuri | 2003-12-01 16:52:49 |
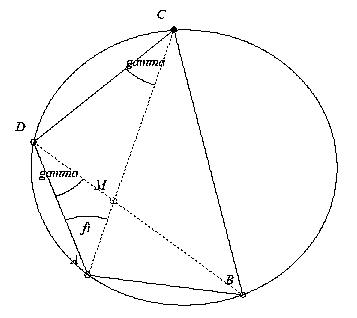
 28. feladat megoldasa
Tekintsuk a lenti abrat. Az AMB ill. az ACB  -ek B-hez tartozo magassaga ill. alapegyenese kozos. Hasonloan szemlelve az AMD es ACD -ek B-hez tartozo magassaga ill. alapegyenese kozos. Hasonloan szemlelve az AMD es ACD  -eket: -eket:
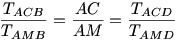
Az AB=AD=a jelolessel:
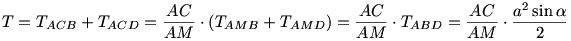
A 'gamma'-val jelolt szogek valoban egyenloek, hisz azonos hosszusagu hurokhoz tartozo keruleti szogek (megfelelo iven). Igy (az implikacio jele nem akar mukodni):
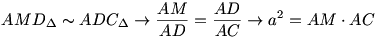
Az a2-re kapott erteket a T-re levezetett kifejezesbe irva a bizanyitando egyenloseget kapjuk.
|
 |
|
| [123] Gyuri | 2003-12-01 14:32:15 |
 Ha mar ugyis Erdekes matekfeladatok a topic, akkor talan megfelelo helyre irom le a kovetkezot.
30. feladat: Ket teljesen intelligens, es egymas eme tulajdonsagat ismero ember beszelgetnek. Egy harmadik szemely meg a tarsalgasuk elott elhelyezett ket cedulat a homlokukon. Mindket emberunk csak a masik fejen levo cedulat latja. A cedulak egyiken ket pozitiv egesz szam osszege, a masikan ugyanannak a ket szamnak a szorzata szerepel. Szerencsere annyit legalabb elarult nekik a harmadik szemely, hogy melyikuk fejen van az osszeg illetve a szorzat. Ezek utan a kovetkezokeppen tarsalognak.
-Nem tudom, mi a ket szam.
-Nem tudom, mi a ket szam.
-Nem tudom, mi a ket szam.
-Nem tudom, mi a ket szam.
-Mar tudom, mi a ket szam.
-Mar en is tudom, mi a ket szam.
Termeszetesen mas informacio nem jut el hozzajuk. Pl. nem allnak tukor elott, nem irjak le egymas szamait papirra, nem irnak emailt, stb.
Remelem mar mindenki tudja, mi a ket szam!
Udv: Gyuri
|
|
| [122] Gyuri | 2003-12-01 14:12:49 |
 Kedves Laszlo!
Ismet akadekoskodnek a 25. feladatra tett megjegyzese kapcsan. Az egyenletrendszer szimmetriaja meg nem biztositek a megoldas szimmetriajara. Legyen

ekkor az
f(x)=y,f(y)=z,f(z)=x
egyenletrendszernek megoldasa a (0,1,-1) szamharmas. De megoldas az
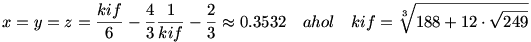
szamharmas is. Udv: Gyuri
|
| Előzmény: [119] lorantfy, 2003-12-01 09:05:35 |
|
| [121] Hajba Károly | 2003-12-01 11:35:26 |
 A következő feladaton csak annyit lehet gondolkodni, mint amennyi időt Örkény egyperceseire fordítunk. Ha valaki tovább gondokozik rajta, csal, mint Rodolfó a bűvész.
29. feladat: A) Kik vannak többen? Nagymamáink dédapjai vagy Dédmamáink nagyapjai? B) Hányan vannak összesen?
HK
|
|
| [120] nadorp | 2003-12-01 10:45:34 |
 Kedves László !
Vázolok egy megoldást a 24.b feladatra.
Legyen X=AB…BC=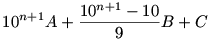 és és
Y=CB…BA=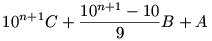
A 7-tel való oszthatóságot elég a 9X és 9Y számokra nézni. Felhasználva még azt, hogy 10 hatványai ugyanazt a maradékot adják 7-tel osztva, mint 3 hatványai, kapjuk:
7 | 2.3n+1A+3(3n-1)B+2C és 7 | 2.3n+1C+3(3n-1)B+2A
3 hatványai rendre a következő maradékokat adják 7-tel osztva: 3,2,6,4,5,1. Ezt felhasználva három esetet különböztetünk meg.
1.eset: n=6k alakú
Ekkor 7 | 3n-1 és 3n+1 7-es maradéka 3, ezért 7 | 6A+2C és 7 | 6C+2A teljesül. De ekkor véve a két szám összegét és különbségét: 7 | 4(A-C) és 7 | 8(A+C), azaz 7 | A-C és 7 | A+C. Ez csak úgy lehet, ha A és C közül az egyik 0, amit kizártunk. Ekkor tehát nincs megoldás.
2.eset: n=6k+5 alakú
Ekkor 3n 7-es maradéka 5 és 3n+1 7-es maradéka 1, ezért 7 | 2A+5B+2C vagy másképpen 7 | 2A+5B+2C-7B=2(A-B+C). Ez teljesül,ha például A=8 B=2 C=1.
3.eset: n 6k és n 6k és n 6k+5 alakú 6k+5 alakú
Mivel 7 | 9X-9Y, ezért 7 | 2(3n+1-1)(A-C) . Ez most csak úgy lehet ha 7 | A-C, azaz A=9 C=2 vagy A=8 C=1 ( vagy ha felcseréljük A és C szerepét, de az most mindegy). Látszik, hogy A C és n ismeretében B egyértelműen meghatározható mod 7. A számolást nem részletezve az alábbi két táblázatot kapjuk:
| n |
1 |
2 |
3 |
4 |
| A |
9 |
9 |
9 |
9 |
| C |
2 |
2 |
2 |
2 |
| B |
5 |
0 |
1 |
2 |
|
| n |
1 |
2 |
3 |
4 |
| A |
8 |
8 |
8 |
8 |
| C |
1 |
1 |
1 |
1 |
| B |
6 |
0 |
4 |
1 |
|
Látszik, hogy n=6k+4 esetén B megegyik A-val vagy C-vel, ami nem lehet. A feladatnak tehát n=6k vagy n=6k+4 esetén nincs megoldása, máskor mindig van.
|
| Előzmény: [110] lorantfy, 2003-11-29 00:33:28 |
|




 0,1n
0,1n  0,1n
0,1n 





 , aki a szorzatot látja, és
, aki a szorzatot látja, és  , aki az összeget látja. S úgy tűnik, a végeredmény attól függ, ki kezdte a párbeszédet, mivel erről nincs infónk.
, aki az összeget látja. S úgy tűnik, a végeredmény attól függ, ki kezdte a párbeszédet, mivel erről nincs infónk.  1 v. prím; többféleképpen tudom a számot összeggé bontani,] nem tudom.
1 v. prím; többféleképpen tudom a számot összeggé bontani,] nem tudom. 
 -ek B-hez tartozo magassaga ill. alapegyenese kozos. Hasonloan szemlelve az AMD es ACD
-ek B-hez tartozo magassaga ill. alapegyenese kozos. Hasonloan szemlelve az AMD es ACD 