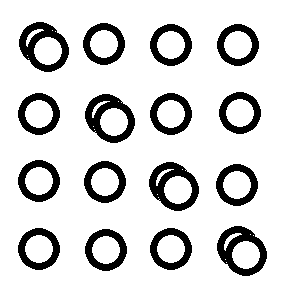|
| [2019] Tappancsa | 2007-04-27 19:08:15 |
 Remélem ez még nem volt.
318. feladat: Gondoltam egy polinomra (p(x)). Az együtthatói pozitív egész számok. Ki tudod-e találni a polinomomat, ha két x értékre hajlandó vagyok megmondani p(x) értékét?
Anikó
|
|
| [2018] HoA | 2007-04-26 16:59:36 |
 Persze. A feladat tehát az, tippeljük meg, legalább hányan állnak kettejük között, ha mobilon beszélnek. Elég 3? Vagy ahhoz hangosan szólni is elég, a mobilozáshoz inkább 6 kell? Stb.
|
| Előzmény: [2017] jonas, 2007-04-26 14:32:31 |
|
|
| [2016] HoA | 2007-04-25 16:43:11 |
 Talán azért érdemes itt foglalkozni ezzel a feladattal, mert szerintem ez a tipikus példája annak, milyen feladatot nem szabad iskolai versenyen feladni. Ugyanis a feladat szövege nem zárja ki azt, hogy Előd és Vali között nem áll senki. És innen nem matematikai, hanem nyelvészeti vagy filozófiai kérdés, van-e értelme 0 ember harmadáról beszélni, vagy a "még akkor is" jelentheti-e azt, hogy nem csökkent az előttem állók száma.
Tehát a megoldás: Ha Előd és Vali között nem áll senki, akkor Vali előtt ( a 0/3 távozása után is) Előd + az Előd előtt állók állnak. Ez csak úgy lehet kétszerese az Előd előtt állóknak, ha Előd előtt 1 ember áll. Ekkor Előd mögött 8-an, tehát Vali mögött 7-en állnak.
Ha előzetes megfontolások nélkül egyenleteket írunk fel, és az Előd előtt állók számát x-szel, az Előd és Vali között állókét y-nal, a Vali mögött állókét pedig z-vel jelöljük, a két megállapítás egyenlete:
y + z + 1 = 8x
2/3 y + 1 +x = 2x
Amiből z = 13/3 y + 7
Itt a feladat kitűzői nyilván elvárják a nyolcadikosoktól, hogy vegyék észre, mivel z egész, y csak 3-mal osztható egész lehet és mint "emberek száma" nem negatív. És itt ismét előjön a kérdés, megengedett-e y=0, ekkor persze z=7, vagy y legkisebb értéke 3 , amiből z=20 a helyes megoldás.
|
| Előzmény: [2013] Matthew, 2007-04-24 21:06:10 |
|
|
|
| [2013] Matthew | 2007-04-24 21:06:10 |
 Üdv mindenkinek!
Tudom,hogy ez a fórum középiskolásoknak van,de éppen ezért szeretnék tőletek segítséget kérni,mert én még csak 8.-os vagyok Tegnap volt a megyei Makkosházi Matematika Versenyen,amin én is elindultam,főleg tapasztalatszerzés céljából.Jókeddvel kezdtem neki a feladatoknak,mert 4 feladatra volt 70 percem,de aztán kiderült,hogy vagy én vagyok gyenge matekból,vagy a feladatok bonyolultabbak.Mindenesetre abban kérnék segítséget,hogy a feladatokat hogyan kellett volna megoldanom,és hogy mi a megoldásuk?.Ha jól tudom(de lehet,hogy rosszul emlékszem),akkor a Kömal is támogatta az iskolát a verseny megrendezésében,tehát lehet,hogy a feladatokat is ismerik éhányan,de azért leírom az elsőt,amire bevallom,közel 35 percem ment el:
Seft Előd és Kár Vali a hosszú sorban állás közben mobilon beszélgetnek.Előd végignézve a soron,megállapítja,hogy "Mögttem nyolcszor annyian vannak,mint előttem." Ezután Vali is "népszámlálást" végez és közli:"Remélem a köztünk lévők harmada itt hagyja és elmegy! De még akkor is kétszer annyian lesztek előttem,mint ahányan előtted vannak."
Legalább hányan lehettek Vali mögött?
Üdv.:Matthew
|
|
| [2012] jonas | 2007-04-24 13:22:18 |
 Hasonló feladat, hogy rakj le húsz érmét az asztalra úgy, hogy minden sorban és minden oszlopban öt legyen.
A megoldás, hogy egymásra kell rakni két érmét:
|
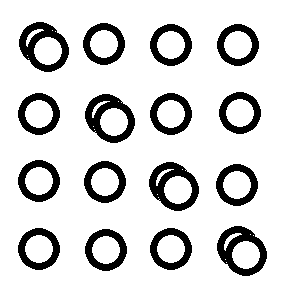 |
| Előzmény: [2008] DirtyD, 2007-04-24 11:48:07 |
|
| [2011] Sirpi | 2007-04-24 13:10:26 |
 Nem akartam bő lére ereszteni a magyarázkodást, képet meg pláne nem akartam hekkelni :-) Szóval köszi a kiegészítést, és tényleg így teljes értékű a megoldás.
|
| Előzmény: [2010] jonas, 2007-04-24 12:25:26 |
|
| [2010] jonas | 2007-04-24 12:25:26 |
 Ha így tálalod a megoldást, akkor rejtvényújság-szaga van. Mondjuk inkább azt, hogy öt általános helyzetű egyenes metszéspontjai. Ez speciálisan a csillagötszöget is tartalmazza, de más helyzet is elképzelhető.
|
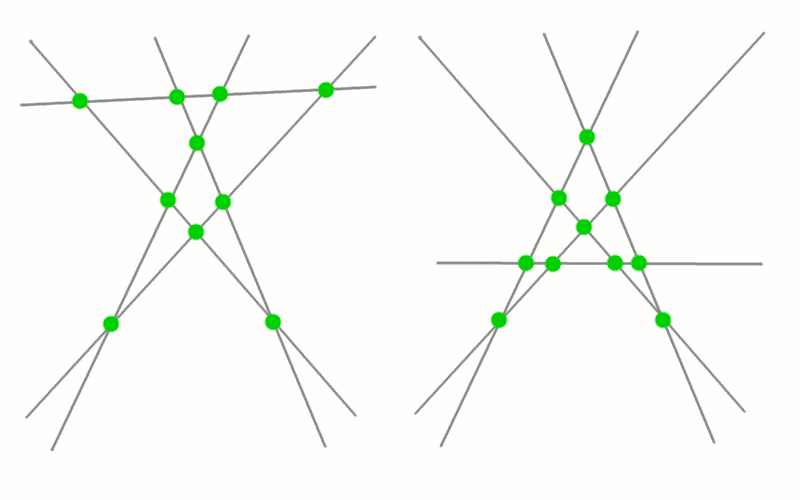 |
| Előzmény: [2009] Sirpi, 2007-04-24 11:53:50 |
|
|
| [2008] DirtyD | 2007-04-24 11:48:07 |
 Sziasztok! Még új vagyok és remélem, hogy nem szerepelt még a következő feladat: Van 10 facsemete, amit 5 sorban úgy kellene elültetni, hogy minden sorba 4 csemete legyen! Lehet nagyon gagyi, de a baráti társaságban még senki nem oldotta meg!
|
|
|
|
|
|
|
|
|
|
| [1999] jonas | 2007-04-21 23:05:14 |
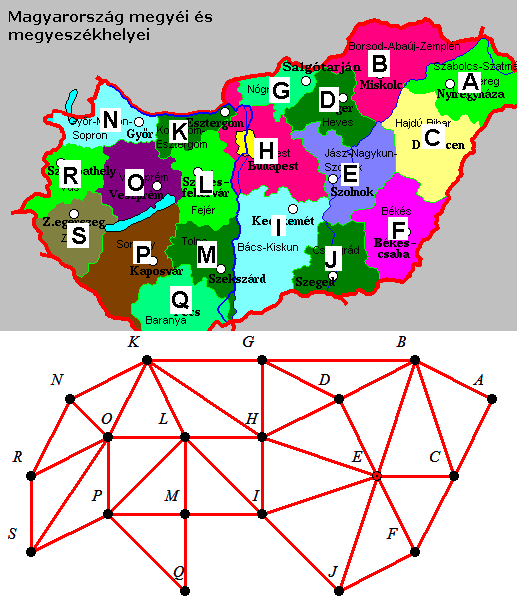
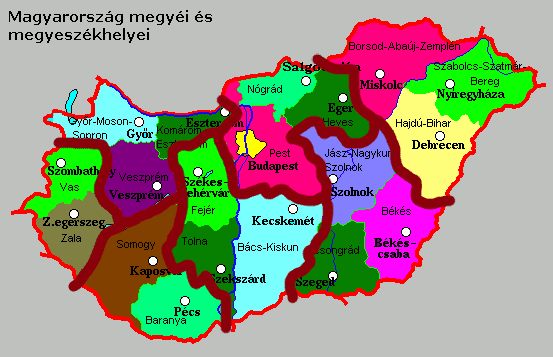
 Ha jól látom, nincs négy páronként szomszédos megye, tehát háromnál többet nem lehet összevonni. Ez azt jelenti, hogy legalább |-19/3-|=7 megye biztosan marad.
Ennyit viszont pont létre lehet hozni.
|
 |
| Előzmény: [1998] lorantfy, 2007-04-21 22:16:26 |
|
| [1998] lorantfy | 2007-04-21 22:16:26 |
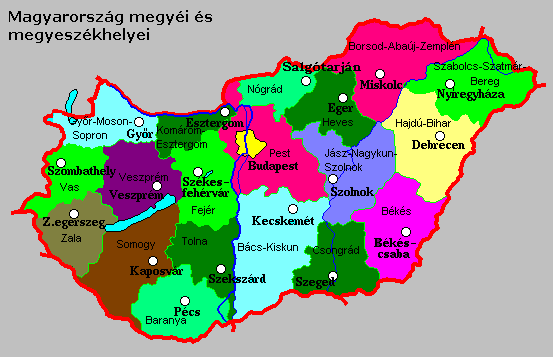
 306. feladat: Legalább hány megye lesz Magyarországon, ha
1. Bármely két megyét összevonhatunk, ha szomszédosak.
2. Nem kerülhet egy új megyébe két régi megye, ha eredetileg nem voltak szomszédosak.
|
 |
|
| [1997] Csimby | 2007-04-19 21:02:54 |
 Ja, megértettem, csak az nem volt világos múltkor, hogy pl. 0,2,4,6,... sorozatból ha beteszed a 2-est az egyik, 4-est a másik halmazba, akkor attól még mi garantálja, hogy 6,8,10,... számtani sorozat nem kerül be teljes egészében az egyik halmazba. Köszi.
|
| Előzmény: [1993] jonas, 2007-04-18 20:54:31 |
|
|