|
| [257] Róbert Gida | 2012-11-09 16:19:47 |
 1 óra 42 percnél Pelikán megadott egy ismert ellenpéldát Shapiro egyenlőtlenségére n=14 (egész) taggal. Némi munkával található "jobb" ellenpélda is, ahol a maximális tag kisebb. Sőt megtalálható ilyen értelemben véve legjobb ellenpélda, ez pedig:
a=[1,31,0,33,0,35,2,35,4,33,4,31,3,30], erre: 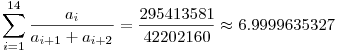
Nem adott viszont ellenpéldát a páratlan n=25-re. Íme a legjobb ellenpélda itt, ez a szörnyeteg: legyen a=[3,14,1,16,0,19,0,23,0,27,2,30,8,28,13,23,15,18,15,13,14,9,13,6,13], ekkor: 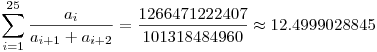
|
|
| [256] Róbert Gida | 2012-11-08 18:41:54 |
 2. szakkör:
http://www.youtube.com/watch?v=bqbBc2AxSyU&feature=g-all-u
|
|
| [255] Hölder | 2012-10-20 00:31:57 |
 Valóban nem lehet látni, hogy mit írnak a táblára, de mindent mond,és ennyi elég is, még akkor is ha éppen ott vagy, mert egyáltalán nem gyorsan írja és mondja a dolgokat. Ettől függetlenül valóban érdemes lenne valamit csinálni a kamerával. Az ötletet, hogy felveszik az előadásokat,üdvözlöm,ha nem kerül túl sokba,érdemes lenne Dobos tanár úróráit is felvenni.
|
| Előzmény: [251] pvong17, 2012-10-07 22:21:10 |
|
| [254] vogel | 2012-10-12 20:56:23 |
 A youtube is konvertálja a videót, az is sokat ronthat. Szintén, a nem HD videót is érdemes HD-ként feltölteni emiatt. (Vagy erre is gondoltál többek közt.)
De a linkeden fél tábla méretű betűkkel írnak. :D
|
| Előzmény: [253] pvong17, 2012-10-11 13:58:24 |
|
| [253] pvong17 | 2012-10-11 13:58:24 |
 Miután megírtam a hozzászólást akkor jutott eszembe, hogy lehet, hogy nem a kamerával van a baj. Ugyanis látszik az első 15 másodpercből, hogy az eredeti videó átment valamilyen videszerkesztő programon (felirat). Tapasztalatból tudom, hogy ha ezeknél a programoknál nincs rendesen beállítva a videó kimeneti formátuma, akkor nagyon el lehet rontani a minőséget. Például a YouTube nyilván HD felbontást is meg tud jeleníteni (16:9-es képarány), szóval a videószerkesztő programban érdemes 16:9, HD felbontást megadni (már ha a kamera egyáltalán HD-ben vette fel az eredeti videót) Bár, aki használt már ilyen programot az általában azt tanulja meg legelőször, hogy hogyan kell a megfelelő kimeneti felbontást megadni...
Másrészt tényleg nem kell HD-ben felvenni, hogy jól látható és szép legyen, elég közelebb is vinni a kamerát. Egy nagyon jó példa itt: http://youtu.be/2XraaWefBd8
|
| Előzmény: [252] lorantfy, 2012-10-10 16:47:49 |
|
|
| [251] pvong17 | 2012-10-07 22:21:10 |
 A felvételen semmit nem lehet látni abból, amit a táblára írnak. Vagy használjatok egy rendes kamerát vagy fel se vegyétek legközelebb. Én általában nem szoktam goromba lenni másokkal, de most (az internet anonimitását kihasználva) azt kell mondjam, hogy ez elég igénytelen munka lett.
Pelikán tanárúrnak viszont köszönöm, bár nem sokat láttam abból, amit a táblára írt. Nem akartam senkit megbántani.
- Egy diák.
|
| Előzmény: [248] Kós Géza, 2012-10-03 18:15:22 |
|
| [250] Róbert Gida | 2012-10-04 00:48:20 |
 Azért az megnyugtató, hogy (szinte) egy olimpiai feladatot sem ismertek fel az olimpiai szakkörön(!)
Pelikán: "Nem olyan könnyű ellenőrizni ezeket, hogy prím-e vagy nem. Iszonyatosan gyorsan nőnek, nem férnek bele a nagy számítógépekbe sem."
Igen, Fermat számokat nézve és a legnagyobb memóriájú szuperszámítógépet akkor F53-ig férnek bele a memóriába. Kérdés, hogy akkor hogyan találnak manapság nagy valódi osztókat még sokkal nagyobb Fermat számokhoz, bizonyítva, hogy összetettek?
9*22543551+1|F2543548=222543548+1
|
| Előzmény: [248] Kós Géza, 2012-10-03 18:15:22 |
|
|
| [248] Kós Géza | 2012-10-03 18:15:22 |
 Videofelvétel a szeptember 21-i olimpiai szakkörről

|
|
| [247] Róbert Gida | 2012-09-12 21:43:00 |
 Csapatban újabb második hely a MEMO-n:
http://index.hu/tudomany/2012/09/12/magyar_siker_a_svajci_diakolimpian/
|
|
| [246] kdano | 2012-09-03 06:26:55 |
 Szerintem eddig is arról beszéltünk, hogy ez így van: a csapatot a csapatvezetők állítják össze, a versenyeredmények alapján mérlegelve, de objektív mérce nélkül. Indoklással (legalábbis a publikum felé) nem nagyon szoktak szolgálni. És a második válogatóverseny eredménye is nyilván azért titkos, hogy a személyi döntéseket ne nagyon lehessen megtámadni (de abban sem vagyok biztos, hogy egzakt pontszámok születnek rá).
A vita inkább arról szólt, hogy jobb-e ez így, vagy inkább objektív rendszer kéne.
|
| Előzmény: [245] egynaivtanar, 2012-09-02 13:00:45 |
|
| [245] egynaivtanar | 2012-09-02 13:00:45 |
 Úgy érzem azóta sem kaptam választ az elég egyértelműen feltett kérdésemre. (Miért titkos a 2. válogatóverseny eredménye (még a versenyzők számára is)?) Ezek után úgy gondolom, hogy valóban az a helyzet, hogy a mostani, vagy leendő döntéshozásban résztvevő tanár vagy tanárok azt visznek ki, akit akarnak mindenféle indoklás nélkül.
|
|
|
| [243] Maga Péter | 2012-08-28 22:08:57 |
 ,,Hm... Ezek szerint mégis más volt a rendszer, most nem hallottam semmilyen magyarázatot semmire...''
Az említett magyarázkodást nekem 40 év távlatából mesélték. Nem tudom, kik felé történt, azt sem, hogy ténylegesen mennyire kellett számot adni a döntésről. Azt is elképzelhetőnek tartom, hogy csak egy szimpla kérdésre kellett válaszolni, amit egy tisztségviselő feltett. ('Hogyhogy? Sose vittünk eddig elsőst!? - Ez a két legjobb.')
|
| Előzmény: [240] egynaivtanar, 2012-08-28 09:52:35 |
|
|
| [241] Kós Géza | 2012-08-28 12:15:45 |
 A csapatvezetők nem saját magukat jelölték ki, a munkájukat a Bolyai Társulat és az Oktatási Államtitkárság is felügyeli. Ne kiáltsunk diktatúrát ott, ahol nincs.
* * * * *
Én nem ismerem a második válogatóverseny (április 23?) eredményeit, de ha ismerném, akkor sem tehetném közzé az érintettek engedélye nélkül. Viszont mindenki leírhatja, hogy ő maga mely feladatokat oldotta meg.
Ha jól tudom, a feladatok ezek voltak:
1. Tekintsük a P(x)=(x+d1)(x+d2)...(x+d9) polinomot, ahol d1,d2,...,d9 kilenc különböző egész szám. Igazoljuk, hogy létezik olyan N egész, hogy minden N -nél nagyobb k egész esetén P(k)-nak van 20-nál nagyobb prím osztója.
(IMO Shortlist 2011, N2)
2. Legyen k a hegyesszögű ABC háromszög köré írt köre, C' és B' rendre az AB és AC oldalak felezőpontjai. Az A-ból induló magasság talppontja D, a háromszög súlypontja S. Az l kör átmegy B'-n és C'-n, és érinti k-t az A-tól különböző E pontban.
Igazoljuk, hogy D, S és E egy egyenesen vannak.
(IMO Shortlist 2011, G4)
3. Az f és g függvények a pozitív egészekhez pozitív egészeket rendelnek. Minden pozitív egész n esetén
fg(n)+1(n)+gf(n)(n)=f(n+1)-g(n+1)+1,
ahol fk(n) jelentése f1(n)=f(n), f2(n)=f(f(n)), f3(n)=f(f(f(n))), ....
Határozzuk meg a feltételeknek megfelelő összes (f;g) függvénypárt.
(IMO Shortlist 2011, A4)
|
| Előzmény: [240] egynaivtanar, 2012-08-28 09:52:35 |
|
| [240] egynaivtanar | 2012-08-28 09:52:35 |
 ",,Továbbá azt azért nehezen hiszem el, hogy Lovász László nem jutott volna ki ha nyilvános a 2. válogató eredménye.''
Nem tudom, akkor volt-e egyáltalán (második) válogató, ezek kb. 40 évvel azelőtt történtek, hogy én az IMO-ban érdekelt voltam. De akkor sem tekintették a válogatási elveket kőbe vésettnek... "
Elnézést, félreérthető volt a kérdésem. Akkor pontosítva: Miért titkos most a 2. válogató?
"csapatvezetésnek komolyan magyarázkodni kellett" Hm... Ezek szerint mégis más volt a rendszer, most nem hallottam semmilyen magyarázatot semmire...
"Ott a pont! A csapatvezetőnek az a dolga, hogy a legerősebbnek vélt csapatot összeállítsa - ebben persze hibázhat, ő is ember. Ha valakit a legjobb (értendő: akitől legjobb olimpiai szereplés elvárható) hatban lát, nem hagyhatja itthon azért, mert év elején úgy gondolta, hogy a legjobb hatba kerüléshez csinálni kell a KöMaL-t. "
Ismerünk a profi sportolók közül is példákat, akiket azért hagytak ki, mert kevésbé lelkesek voltak. Igen, ha valaki nem csinálja rendesen a dolgát, akkor miért nem azt viszik el, aki lelkes és tesz a dologért és hosszabb távon több lehetőség van benne.
A nagypolitikában, ha 1-2 ember indoklás nélkül irányít TITKOSAN azt diktatúrának hívják. Van valami hasonlóság a mostani helyzettel... Most ezek szerint arról vitatkozunk, hogy a diktatúra a lehető legjobb rendszer? A történelem számtalanszor bebizonyította, hogy nem. Bizonyos diktatúrák csúfos kudarcot értek. Esetleg itt is meg lehet ezt várni...
|
|
| [239] Maga Péter | 2012-08-28 08:32:26 |
 ,,biztos vagyok benne, hogy a csapatvezetők csalódtak a versenyzőkben, hogy nem csinálták a kömalt, de ettől még találhatták őket legalkalmasabb csapattagoknak''
Ott a pont! A csapatvezetőnek az a dolga, hogy a legerősebbnek vélt csapatot összeállítsa - ebben persze hibázhat, ő is ember. Ha valakit a legjobb (értendő: akitől legjobb olimpiai szereplés elvárható) hatban lát, nem hagyhatja itthon azért, mert év elején úgy gondolta, hogy a legjobb hatba kerüléshez csinálni kell a KöMaL-t.
---
A feladatleírások minőségén sírni lehet, tisztelet a nagyon kevés kivételnek (Janzer Olivér dolgozatait lehetne küldeni a nyomdába, úgy, ahogy vannak). Szerintem kell a B a jelenlegi színvonalon.
|
| Előzmény: [237] kdano, 2012-08-28 04:53:15 |
|
| [238] Maga Péter | 2012-08-28 08:20:29 |
 ,,Továbbá azt azért nehezen hiszem el, hogy Lovász László nem jutott volna ki ha nyilvános a 2. válogató eredménye.''
Nem tudom, akkor volt-e egyáltalán (második) válogató, ezek kb. 40 évvel azelőtt történtek, hogy én az IMO-ban érdekelt voltam. De akkor sem tekintették a válogatási elveket kőbe vésettnek...
Annak idején nekünk Pelikán József úgy mesélte, hogy akkoriban volt egy szabály (vagy inkább elv), valami olyasmi, hogy csak végzőst vihetnek (vagy harmadikost és negyedikest, nem emlékszem pontosan). A csapatvezetésnek komolyan magyarázkodni kellett, hogy kivihessenek két gimis elsőst. Nem tudtak egyébbel előállni, mint hogy 'ez a két legjobb'. Ha a szabály kőbe lett volna vésve, akkor a két legjobb itthon marad.
,,Nem lehet a fejünket a földbe dugni, észre kell venni, hogy romlik a teljesítmény. Ha semmi változást sem csinálunk, mert ki-ki lát egy-egy picike hibát benne, akkor ez így marad továbbra is...''
Ebben egyetértek. De váltig állítom, hogy a gyenge szereplésnek nem a válogatási szisztéma az oka. Meg vagyok róla győződve, hogy lényegesen jobb eredményt idén semmilyen hatosfogat nem ért volna el. Ugyanez a rendszer nem is oly rég, a 90-es években, a 2000-es évek elején még rendre top 10 csapatokat kovácsolt.
|
| Előzmény: [236] egynaivtanar, 2012-08-27 14:37:55 |
|
| [237] kdano | 2012-08-28 04:53:15 |
 én nem érzem olyan egyértelműnek, hogy ez kötelező feltétel volt: én továbbra is hajlok arra, hogy ez egy kétségbeesett próbálkozás volt a diákok kömalozásra bírására. például hivatalosan (írásban) biztos nincs olyan szabály, hogy csak az lehet olimpikon, aki csinálja a kömal b-t. én nem csináltam 11-12-ben.
és az, hogy elvárja, szintén nem sokat jelent: csalódik bennük, ha nem kömaloznak? biztos vagyok benne, hogy a csapatvezetők csalódtak a versenyzőkben, hogy nem csinálták a kömalt, de ettől még találhatták őket legalkalmasabb csapattagoknak. (például ha a versenyen semmi probléma nem volt a feladatleírásukkal, az helyből semlegesíti az egyik érvet a B küldése mellett.)
Peti: a feladatleírások minőségét nem ismerem, de azt egyrészt az A feladatok leírásával is lehet gyakorolni (és egy hosszabb A-megoldás leírása felér egy-két B-feladattal is), másrészt 8-9-10-edikben az A még gyakran nehéz a későbbi olimpikonnak is, én úgy képzelem, hogy olyankor a B-t küldve szintén gyakorolja a leírást. (persze tudom, egy tizenegyedikes ezzel már kicsit elkésett)
A B pontversenynél meg vannak relevánsabb feladatsorok is az olimpiai készülésre, ezért nem tartanám szerencsésnek explicite feltételnek szabni azt.
|
| Előzmény: [236] egynaivtanar, 2012-08-27 14:37:55 |
|
| [236] egynaivtanar | 2012-08-27 14:37:55 |
 Elképzelhetetlennek tartjátok, hogy egy 9.es is részt vegyen versenyen kívül az OKTV-n? Ha pedig minden versenyt meg tud írni, akkor miért ne jutna ki egy pontozásos rendszerben is? Továbbá azt azért nehezen hiszem el, hogy Lovász László nem jutott volna ki ha nyilvános a 2. válogató eredménye. Szerintem ha valaki 9.esként akkora zseni, hogy ki kell vinni, akkor ezt a 2. válogató eltitkolása nélkül is meg lehet tenni.
Úgy érzem megerősítést nyert, hogy FELTÉTEL, KÖTELEZŐ volt a Kömal B oldása. Ezek szerint mégsem annyira vegyes a csapatvezetők e téren való gondolkodása... Továbbra is érdekelne, hogy hogyan lehetséges kijutni a feltétel teljesítése nélkül.
Nem lehet a fejünket a földbe dugni, észre kell venni, hogy romlik a teljesítmény. Ha semmi változást sem csinálunk, mert ki-ki lát egy-egy picike hibát benne, akkor ez így marad továbbra is...
|
|
| [235] m2mm | 2012-08-27 12:58:41 |
 "idén 1., 2., 4.) inkább B, mint A szintű". Ez igaz, viszont amint már említettem (5 pontos) egyenlőtlenségekkel és ilyen tipikus függvényegyenletekkel nem lehetett idén B-ben találkozni, talán ezért nem mentek (ez nem a KöMaL szidása akar lenni!, csak egy remélhető válasz az okra). Az valóban nem túl pozitív, ha általánosan a B-szintűek se mennek.
|
| Előzmény: [231] Maga Péter, 2012-08-27 12:19:28 |
|
| [234] m2mm | 2012-08-27 12:53:41 |
 A B-jelű pontversenyt én is így látom, mondjuk szerintem az 5 pontosokat is illő legalább 90 százalékban megoldani.
Továbbá el is veszi az időt az A-tól, pl. ha egy geometria példát akarunk minden hiányosság nélkül beküldeni vagy beraknak olyan 5 pontos B-példát ami nehezebb az A-jelűeknél(pl. B. 4380. nehezebb volt szerintem mindhárom szeptemberi A-nál - ezt a megoldók száma is mutatja....). Meg azért a B-példák lezúzása és leírása mindig elvesz legalább 1-3, ha nehezebb példa is van, akkor 4-5 délutánnyit. Vagy olyan példa is van, aminek a leírása egy délután-bár lehet ez csak az én hibám. Ez mondjuk versenyidőszakban/felvételinél/érettséginél fontos tud lenni az A-példák oldása kapcsán, márpedig ott lehet olyan feladatokkal találkozni, amelyek IMO 3,6 szintjénél vannak, vagy RMM kb. összes példájánál.
|
| Előzmény: [230] kdano, 2012-08-27 06:27:23 |
|
